京都大学 理系 2020年度 第3問 解説
問題編
問題
$k$ を正の実数とする。座標空間において、原点 O を中心とする半径 $1$ の球面上の4点 A, B, C, D が次の関係式を満たしている。
\begin{eqnarray} & & \overrightarrow{ \mathrm{ OA } }\cdot \overrightarrow{ \mathrm{ OB } } =\overrightarrow{ \mathrm{ OC } }\cdot \overrightarrow{ \mathrm{ OD } } =\frac{1}{2}, \\[5pt] & & \overrightarrow{ \mathrm{ OA } }\cdot \overrightarrow{ \mathrm{ OC } } =\overrightarrow{ \mathrm{ OB } }\cdot \overrightarrow{ \mathrm{ OC } } =-\frac{\sqrt{6} }{4}, \\[5pt] & & \overrightarrow{ \mathrm{ OA } }\cdot \overrightarrow{ \mathrm{ OD } } =\overrightarrow{ \mathrm{ OB } }\cdot \overrightarrow{ \mathrm{ OD } } =k \\[5pt] \end{eqnarray} このとき、 $k$ の値を求めよ。ただし、座標空間の点 X, Y に対して、 $\overrightarrow{ \mathrm{ OX } }\cdot \overrightarrow{ \mathrm{ OY } }$ は、 $\overrightarrow{ \mathrm{ OX } }$ と $\overrightarrow{ \mathrm{ OY } }$ の内積を表す。
考え方
一般的に座標を置いて計算するのは大変です。まずは、内積で与えられた条件が、図形のどのような性質に置き換えられるかを考えます。図形として考えると計算はかなり減りますが、空間図形では図形として考えるのも大変です。適宜、適当な平面で切って考えてみましょう。
解答編
問題
$k$ を正の実数とする。座標空間において、原点 O を中心とする半径 $1$ の球面上の4点 A, B, C, D が次の関係式を満たしている。
\begin{eqnarray} & & \overrightarrow{ \mathrm{ OA } }\cdot \overrightarrow{ \mathrm{ OB } } =\overrightarrow{ \mathrm{ OC } }\cdot \overrightarrow{ \mathrm{ OD } } =\frac{1}{2}, \\[5pt] & & \overrightarrow{ \mathrm{ OA } }\cdot \overrightarrow{ \mathrm{ OC } } =\overrightarrow{ \mathrm{ OB } }\cdot \overrightarrow{ \mathrm{ OC } } =-\frac{\sqrt{6} }{4}, \\[5pt] & & \overrightarrow{ \mathrm{ OA } }\cdot \overrightarrow{ \mathrm{ OD } } =\overrightarrow{ \mathrm{ OB } }\cdot \overrightarrow{ \mathrm{ OD } } =k \\[5pt] \end{eqnarray} このとき、 $k$ の値を求めよ。ただし、座標空間の点 X, Y に対して、 $\overrightarrow{ \mathrm{ OX } }\cdot \overrightarrow{ \mathrm{ OY } }$ は、 $\overrightarrow{ \mathrm{ OX } }$ と $\overrightarrow{ \mathrm{ OY } }$ の内積を表す。
解答
A, B, C, D は原点を中心とした半径 $1$ の球面上の点であるから、1つ目の関係式より、三角形 OAB も三角形 OCD も正三角形であることがわかる。
2つ目の関係式から、三角形 OAC と三角形 OBC が合同であることがわかる(2組の辺とその間の角がそれぞれ等しいため)。よって、線分 AB を垂直に二等分する平面上に点 C があることがわかる。この平面を $\alpha$ とおく。
同様に、3つ目の関係式から、 D も平面 $\alpha$ 上にあることがわかる。
線分 AB の中点を M とすると、 OM の長さは1辺が $1$ の正三角形の高さなので $\dfrac{\sqrt{3} }{2}$ である。また、\[
\overrightarrow{ \mathrm{ OM } }=\dfrac{1}{2} \left(\overrightarrow{ \mathrm{ OA } }+\overrightarrow{ \mathrm{ OB } }\right) \]と表すことができ、 M も平面 $\alpha$ 上にあることがわかる。
ここで、
\begin{eqnarray}
& &
\overrightarrow{ \mathrm{ OM } }\cdot \overrightarrow{ \mathrm{ OC } } \\[5pt]
&=&
\frac{1}{2} \overrightarrow{ \mathrm{ OA } } \cdot \overrightarrow{ \mathrm{ OC } }
+\frac{1}{2} \overrightarrow{ \mathrm{ OB } } \cdot \overrightarrow{ \mathrm{ OC } } \\[5pt]
&=&
-\dfrac{\sqrt{6} }{4}
\end{eqnarray}と計算できるので、\[ \cos\angle \mathrm{ COM }=-\frac{\sqrt{6} }{4}\cdot\frac{2}{\sqrt{3} }=-\frac{\sqrt{2} }{2} \]となるから、 $\angle\mathrm{COM}=135^{\circ}$ となることがわかる。
また、
\begin{eqnarray}
& &
\overrightarrow{ \mathrm{ OM } }\cdot \overrightarrow{ \mathrm{ OD } } \\[5pt]
&=&
\frac{1}{2} \overrightarrow{ \mathrm{ OA } } \cdot \overrightarrow{ \mathrm{ OC } }
+\frac{1}{2} \overrightarrow{ \mathrm{ OB } } \cdot \overrightarrow{ \mathrm{ OC } } \\[5pt]
&=&
k
\end{eqnarray}である。 $k\gt 0$ なので、平面 $\alpha$ でこの球を切断すると、次のような断面となる。
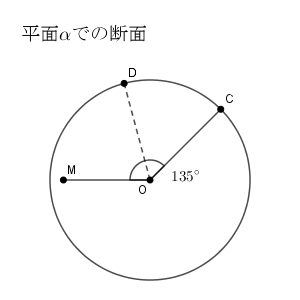
なお、 $\angle \mathrm{ COD }=60^{\circ}$ となる D はもう一つあるが、その点は内積が負になるから $k\gt 0$ という条件に合わない。
さて、こうして
\begin{eqnarray}
k
&=&
\overrightarrow{ \mathrm{ OM } }\cdot \overrightarrow{ \mathrm{ OD } } \\[5pt]
&=&
\frac{\sqrt{3} }{2}\cos 75^{\circ} \\[5pt]
&=&
\frac{\sqrt{3} }{2}\left( \frac{\sqrt{2} }{2}\cdot\frac{\sqrt{3} }{2} -\frac{\sqrt{2} }{2}\cdot\frac{1}{2} \right)\\[5pt]
&=&
\frac{3\sqrt{2}-\sqrt{6} }{8}
\end{eqnarray}と求められる。
(終)





