京都大学 理系 2019年度 第3問 解説
問題編
問題
鋭角三角形 ABC を考え、その面積を S とする。 $0\lt t\lt 1$ を満たす実数 $t$ に対し、線分 AC を $t:1-t$ に内分する点を Q、線分 BQ を $t:1-t$ に内分する点を P とする。実数 t がこの範囲を動くときに点 P の描く曲線と、線分 BC によって囲まれる部分の面積を、 S を用いて表せ。
考え方
よくわからない曲線で囲まれた部分の面積なので、積分を使うことが予想できます。 $t$ を媒介変数だと思って積分することを考えましょう。
$t=0,1$ とはなりませんが、限りなく近づけていくと考えてみると、 $t=0$ のときは、点 P は点 B と一致し、 $t=1$ のときは、点 P は点 C と一致します。 BC を $x$ 軸上に乗せて、点 P の座標を $t$ を使って書けば、何を積分すればいいかがわかるでしょう。
解答編
問題
鋭角三角形 ABC を考え、その面積を S とする。 $0\lt t\lt 1$ を満たす実数 $t$ に対し、線分 AC を $t:1-t$ に内分する点を Q、線分 BQ を $t:1-t$ に内分する点を P とする。実数 t がこの範囲を動くときに点 P の描く曲線と、線分 BC によって囲まれる部分の面積を、 S を用いて表せ。
解答
三角形 ABC を回転・対称・平行移動することで、 $\mathrm{ A }(a,b)$, $\mathrm{ B }(0,0)$, $\mathrm{ C }(c,0)$ となるようにする。ここで、 $b\gt 0$, $c\gt 0$ とできる。三角形 ABC は鋭角三角形であるから、 $0\lt a\lt c$ が成り立つ。また、 $S=\dfrac{bc}{2}$ である。
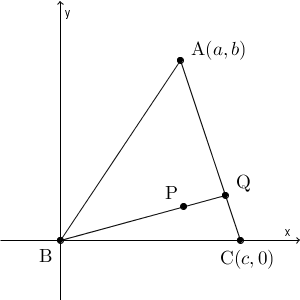
このとき、点 Q の座標は
\begin{eqnarray}
& &
\left((1-t)a+tc,(1-t)b\right) \\[5pt]
&=&
\left((c-a)t+a,-bt+b\right)
\end{eqnarray}であり、点 P の座標は
\begin{eqnarray}
\left((c-a)t^2+at,-bt^2+bt\right)
\end{eqnarray}となる。ここで、 $x=(c-a)t^2+at$ とおくと、\[ \frac{dx}{dt}=2(c-a)t+a \]であり、 $0\lt a \lt c$ なので、この値は $0\lt t\lt 1$ で正である。よって、この範囲で、 $x$ は $t$ について単調増加である。また、 $t=0,1$ とすると、それぞれ $x=0,c$ となる。
$y=-bt^2+bt$ とすると、点 P の構成方法から、 $y$ は $0\lt t\lt 1$ で正である。
以上から、点 P の描く曲線と、線分 BC によって囲まれる部分の面積は、\[ \int_0^c y dx \]で表すことができる。これを $t$ を使って変形すると
\begin{eqnarray}
& &
\int_0^c y dx \\[5pt]
&=&
\int_0^1 (-bt^2+bt)\{2(c-a)t+a\} dt \\[5pt]
&=&
b\int_0^1 \{ -2t^3(c-a)+(-a+2c-2a)t^2+at \} dt \\[5pt]
&=&
b \Big[-\frac{t^4}{2}(c-a)+(2c-3a)\frac{t^3}{3}+\frac{1}{2}at^2 \Big]_0^1 \\[5pt]
&=&
b \left\{-\frac{1}{2}(c-a)+\frac{2c-3a}{3}+\frac{a}{2}\right\} \\[5pt]
&=&
\frac{bc}{6} \\[5pt]
&=&
\frac{S}{3} \\[5pt]
\end{eqnarray}と表すことができる。
(終)





