京都大学 理系 2018年度 第6問 解説
問題編
問題
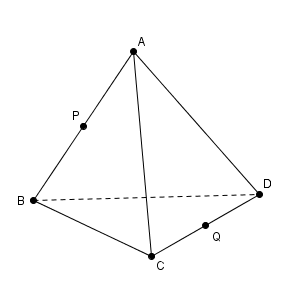
四面体 ABCD は $\mathrm{ AC }=\mathrm{ BD }$, $\mathrm{ AD }=\mathrm{ BC }$ を満たすとし、辺 AB の中点を P、辺 CD の中点を Q とする。
(1) 辺 AB と線分 PQ は垂直であることを示せ。
(2) 線分 PQ を含む平面 $\alpha$ で四面体 ABCD を切って2つの部分に分ける。このとき、2つの部分の体積は等しいことを示せ。
考え方
(1)はベクトルを使い、内積を考えれば示すことができます。問題は(2)です。
(2)は、ベクトルを使って示すことは難しいでしょう。図形の性質を用いて、四面体の対称性を示さないといけません。
解答編
問題
四面体 ABCD は $\mathrm{ AC }=\mathrm{ BD }$, $\mathrm{ AD }=\mathrm{ BC }$ を満たすとし、辺 AB の中点を P、辺 CD の中点を Q とする。
(1) 辺 AB と線分 PQ は垂直であることを示せ。
解答
(1)
$\overrightarrow{ \mathrm{ AB } }=\vec{b}$, $\overrightarrow{ \mathrm{ AC } }=\vec{c}$, $\overrightarrow{ \mathrm{ AD } }=\vec{d}$ とする。このとき、\[ \overrightarrow{ \mathrm{ AP } }=\frac{1}{2}\vec{b},\ \overrightarrow{ \mathrm{ AQ } }=\frac{1}{2}(\vec{c}+\vec{d}) \]と書けるので、 $\overrightarrow{ \mathrm{ AB } }$ と $\overrightarrow{ \mathrm{ PQ } }$ の内積は
\begin{eqnarray}
\overrightarrow{ \mathrm{ AB } } \cdot \overrightarrow{ \mathrm{ PQ } }
&=&
\vec{b}\cdot \frac{\vec{c}+\vec{d}-\vec{b} }{2}\\[5pt]
&=&
\frac{\vec{b}\cdot (\vec{c}+\vec{d})-|\vec{b}|^2}{2} \quad \cdots (*)\\[5pt]
\end{eqnarray}となる。
ここで、 $\mathrm{ AC }=\mathrm{ BD }$ より\[ |\vec{c}|^2 = |\vec{d}-\vec{b}|^2 \]が成り立つ。また、 $\mathrm{ AD }=\mathrm{ BC }$ より\[ |\vec{d}|^2 = |\vec{c}-\vec{b}|^2 \]が成り立つ。これらを辺々加えると
\begin{eqnarray}
|\vec{c}|^2+|\vec{d}|^2 &=& |\vec{d}-\vec{b}|^2+|\vec{c}-\vec{b}|^2 \\[5pt]
\vec{b}\cdot\vec{c}+\vec{b}\cdot\vec{d} &=& |\vec{b}|^2 \\[5pt]
\end{eqnarray}が成り立つ。これを $(*)$ に代入すれば、\[ \overrightarrow{ \mathrm{ AB } } \cdot \overrightarrow{ \mathrm{ PQ } }=0 \]であることがわかる。
よって、辺 AB と線分 PQ は垂直である。
(終)
別解
(1) の別解
三角形 ACD と三角形 BDC について、
$\mathrm{ AC }=\mathrm{ BD }$ (仮定より)…(a)
$\mathrm{ AD }=\mathrm{ BC }$ (仮定より)…(b)
$\mathrm{ CD }=\mathrm{ DC }$ (共通)…(c)
(a)(b)(c)より、3組の辺がそれぞれ等しいので、三角形 ACD と三角形 BDC は合同である。これより、
$\angle \mathrm{ ACQ }=\angle \mathrm{ BDQ }$ …(d)
が成り立つ。
三角形 ACQ と三角形 BDQ について
$\mathrm{ CQ }=\mathrm{ DQ }$ (Q は辺 CD の中点)…(e)
(a)(d)(e)より、2組の辺とその間の角がそれぞれ等しいので、三角形 ACQ と三角形 BDQ は合同である。これより、 $\mathrm{ AQ }=\mathrm{ BQ }$ なので、三角形 ABQ は二等辺三角形。P は辺 AB の中点なので、辺 AB と PQ は垂直である。
(終)
解答編 つづき
問題
(2) 線分 PQ を含む平面 $\alpha$ で四面体 ABCD を切って2つの部分に分ける。このとき、2つの部分の体積は等しいことを示せ。
解答

(1)と同様にすると、三角形 ABC と三角形 BAD が合同であることもわかり、三角形 BCP と三角形 ADP が合同であることもわかるので、 $\mathrm{ PC }=\mathrm{ PD }$ が成り立ち、辺 CD も PQ と垂直であることがわかる。
これらのことから、PQ に垂直な平面のうち、点P を含むものを平面 $\beta_P$, 点Q を含むものを平面 $\beta_Q$ とすると、辺 AB は平面 $\beta_P$ に含まれ、辺 CD は平面 $\beta_Q$ に含まれることがわかる。
今、 線分 PQ と垂直で、線分 PQ (両端の点を除く)と共有点を持つ平面 $\beta$ でこの四面体を切ったとする。

辺 BC, AC, AD, BDは、それぞれ、平面 $\beta_P$ と平面 $\beta_Q$ の両方に共有点を持っているため、断面と交わる。よって、交点を、上の図のように E, F, G, H とおく。
平面 $\beta_P$ と平面 $\beta_Q$ と平面 $\beta$ が平行であることから、各面にできる切り口は、辺 AB または辺 CD と平行である。よって、四角形 EFGH は平行四辺形となる。この平行四辺形の対角線の交点を R とおく。
平面 $\beta_P$ と平面 $\beta_Q$ と平面 $\beta$ が平行であることから、 $\mathrm{ BC }:\mathrm{ BE }=\mathrm{ AD }:\mathrm{ AG }$ が成り立ち、 $\mathrm{ BC }=\mathrm{ AD }$ より、 $\mathrm{ BE }=\mathrm{ AG }$ が成り立つ。これと $\mathrm{ BP }=\mathrm{ AP }$, $\angle \mathrm{ EBP }=\angle \mathrm{ GAP }$ から、三角形 BPE と三角形 APG が合同であることがわかる。
よって、 $\mathrm{ PE }=\mathrm{ PG }$ だから、 EG と PR は垂直である。同様に、 FH も PR と垂直である。
このことから、 PR が平面 $\beta$ に垂直であることがわかる。もともと、 PQ は平面 $\beta$ に垂直だったので、これは、 PQ が平行四辺形 EFGH の対角線の交点を通ることを意味している。
これは各断面について成り立ち、平行四辺形は対角線の交点を中心とした点対称な図形であることから、この四面体 ABCD は線分 PQ を軸に180度回転すると、もとの四面体と一致する。よって、 PQ を含む平面でこの四面体を切断すると同じ立体が2つできるので、体積は等しい。
(終)





