京都大学 理系 2018年度 第3問 解説
問題編
問題
$\alpha$ は $0\lt \alpha \leqq\dfrac{\pi}{2}$ を満たす定数とし、四角形 ABCD に関する次の2つの条件を考える。
(i) 四角形 ABCD は半径 $1$ の円に内接する。
(ii) $\angle \mathrm{ ABC }=\angle \mathrm{ DAB }=\alpha$条件(i)と(ii) を満たす四角形のなかで、4辺の長さの積\[ k=\mathrm{ AB }\cdot\mathrm{ BC }\cdot\mathrm{ CD }\cdot\mathrm{ DA } \]が最大となるものについて、 k の値を求めよ。
考え方
(i)の条件があるので、正弦定理を使って、角度を用いて辺の長さを表すことを考えましょう。ある角度を変数として、 k を変形していきます。
最後は、最大値をとることがあるか、きちんと述べるようにしましょう。
解答編
問題
$\alpha$ は $0\lt \alpha \leqq\dfrac{\pi}{2}$ を満たす定数とし、四角形 ABCD に関する次の2つの条件を考える。
(i) 四角形 ABCD は半径 $1$ の円に内接する。
(ii) $\angle \mathrm{ ABC }=\angle \mathrm{ DAB }=\alpha$条件(i)と(ii) を満たす四角形のなかで、4辺の長さの積\[ k=\mathrm{ AB }\cdot\mathrm{ BC }\cdot\mathrm{ CD }\cdot\mathrm{ DA } \]が最大となるものについて、 k の値を求めよ。
解答
条件(i),(ii) より、四角形 ABCD は $\mathrm{ AD }=\mathrm{ BC }$ の等脚台形である。
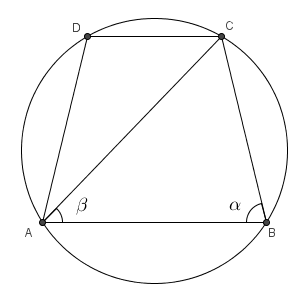
$\angle \mathrm{ CAB }=\beta$ とおく。正弦定理より
\begin{eqnarray}
\mathrm{ AB } &=& 2\sin(\pi-\alpha-\beta) = 2\sin(\alpha+\beta) \\[5pt]
\mathrm{ BC } &=& 2\sin\beta \\[5pt]
\mathrm{ CD } &=& 2\sin(\alpha-\beta) \\[5pt]
\mathrm{ DA } &=& 2\sin\beta \\[5pt]
\end{eqnarray}なので、
\begin{eqnarray}
k
&=&
\mathrm{ AB }\cdot\mathrm{ BC }\cdot\mathrm{ CD }\cdot\mathrm{ DA } \\[5pt]
&=&
16 \sin^2\beta \sin(\alpha+\beta) \sin(\alpha-\beta) \\[5pt]
&=&
16 \cdot \frac{1-\cos 2\beta}{2} \cdot \frac{\cos 2\beta -\cos 2\alpha}{2} \\[5pt]
&=&
4 (1-\cos 2\beta)(\cos 2\beta -\cos 2\alpha) \\[5pt]
&=&
-4\cos^2 2\beta +(4+4\cos 2\alpha)\cos\beta -4\cos 2\alpha \\[5pt]
&=&
-4\left(\cos 2\beta -\frac{1+\cos 2\alpha}{2}\right)^2 +\left(1+\cos 2\alpha\right)^2 -4\cos 2\alpha \\[5pt]
&=&
-4\left(\cos 2\beta -\frac{1+\cos 2\alpha}{2}\right)^2 +(\cos 2\alpha-1)^2 \quad \cdots(*)\\[5pt]
\end{eqnarray}と変形できる。
ここで、条件(i)(ii) を満たしたまま、 AB と CD を近づけていくと、 $\beta$ は $0$ に限りなく近づけることができ、 AB と CD を遠ざけて CD を短くしていくと、 $\beta$ は限りなく $\alpha$ に近づけることができる。
よって、 $\beta$ は $0$ から $\alpha$ までの値を取りうる(両端は除く)。 $0\lt \alpha\leqq \dfrac{\pi}{2}$ より、 $\cos 2\beta$ は $\cos 2\alpha$ から $\cos 0=1$ までの値を取りうる(両端は除く)。ここで\[
\cos 2\alpha \lt \frac{1+\cos 2\alpha}{2} \lt 1 \]なので、\[\cos 2\beta =\frac{1+\cos 2\alpha}{2}\]を満たす $\beta$ が存在する。
このことと $(*)$ より、 $k$ の最大値は、 $(\cos 2\alpha-1)^2$ であることがわかる。
(終)





