京都大学 理系 2013年度 第1問 解説
問題編
問題
平行四辺形 ABCD において、辺 AB を $1:1$ に内分する点を E、辺 BC を $2:1$ に内分する点を F、辺 CD を $3:1$ に内分する点を G とする。線分 CE と線分 FG の交点を P とし、線分 AP を延長した直線と辺 BC の交点を Q とするとき、比 AP:PQ を求めよ。
考え方
よく見かける設定で、何をすべきかはすぐにわかります。計算も大変ではありません。これを1問目にもってきてくれるのは、かなり親切です。
解答編
問題
平行四辺形 ABCD において、辺 AB を $1:1$ に内分する点を E、辺 BC を $2:1$ に内分する点を F、辺 CD を $3:1$ に内分する点を G とする。線分 CE と線分 FG の交点を P とし、線分 AP を延長した直線と辺 BC の交点を Q とするとき、比 AP:PQ を求めよ。
解答
$\vec{b}=\overrightarrow{ \mathrm{ AB } }$, $\vec{d}=\overrightarrow{ \mathrm{ AD } }$ とする。
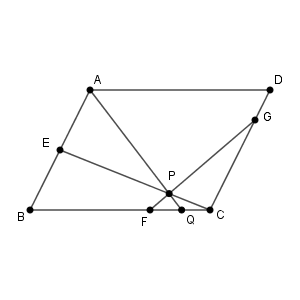
このとき、 $\overrightarrow{ \mathrm{ AE } }=\dfrac{1}{2}\vec{b}$, $\overrightarrow{ \mathrm{ AF } }=\vec{b}+\dfrac{2}{3}\vec{d}$, $\overrightarrow{ \mathrm{ AG } }=\dfrac{1}{4}\vec{b}+\vec{d}$ となる。
$\mathrm{ CP:PE }=s:(1-s)$ とすると
\begin{eqnarray}
\overrightarrow{ \mathrm{ AP } }
&=&
(1-s) \overrightarrow{ \mathrm{ AC } } +s\overrightarrow{ \mathrm{ AE } } \\[5pt]
&=&
(1-s) (\vec{b}+\vec{d}) +s\cdot\frac{1}{2}\vec{b} \\[5pt]
&=&
\left(1-\frac{s}{2}\right)\vec{b}+(1-s)\vec{d} \\[5pt]
\end{eqnarray}となる。
$\mathrm{ FP:PG }=t:(1-t)$ とすると
\begin{eqnarray}
\overrightarrow{ \mathrm{ AP } }
&=&
(1-t) \overrightarrow{ \mathrm{ AF } } +t\overrightarrow{ \mathrm{ AG } } \\[5pt]
&=&
(1-t) \left(\vec{b}+\frac{2}{3}\vec{d}\right) +t\left( \frac{1}{4}\vec{b}+\vec{d} \right) \\[5pt]
&=&
\left(1-\frac{3}{4}t\right)\vec{b}+\left(\frac{2}{3}+\frac{1}{3}t\right)\vec{d} \\[5pt]
\end{eqnarray}となる。
$\vec{b}$, $\vec{d}$ はどちらも $\vec{0}$ でなく、互いに平行でもないので、
\begin{eqnarray}
\left\{
\begin{array}{l}
1-\dfrac{s}{2}=1-\dfrac{3}{4}t \\[5pt]
1-s = \dfrac{2}{3}+\dfrac{1}{3}t
\end{array}
\right.
\end{eqnarray}が成り立つ。1つ目の式から $s=\dfrac{3}{2}t$ が成り立つので、これを2つ目の式に代入すれば
\begin{eqnarray}
1-\frac{3}{2}t &=& \frac{2}{3}+\frac{1}{3}t \\[5pt]
\frac{11}{6}t &=& \frac{1}{3} \\[5pt]
t &=& \frac{2}{11} \\[5pt]
\end{eqnarray}となる。よって、\[ \overrightarrow{ \mathrm{ AP } }=\frac{19}{22}\vec{b}+\frac{8}{11}\vec{d} \]と表せる。
$\overrightarrow{ \mathrm{ AQ } }$ は、実数 $k$ を用いて、 $k\overrightarrow{ \mathrm{ AP } }$ と書ける。 Q は辺 BC 上の点なので、 $\vec{b}$ の係数は $1$ となるから、 $k=\dfrac{22}{19}$ である。よって、\[ \mathrm{ AP:PQ }=19:3 \]となる。
(解答終)
おまけ
この問題を中学入試と思って解く動画です。





