京都大学 理系 2006年度後期 第4問 解説
問題編
【問題】
平面上の点Oを中心とし半径1の円周上に相異なる3点A,B,Cがある。$\triangle \mathrm{ ABC }$の内接円の半径rは$\displaystyle \frac{1}{2}$以下であることを示せ。
【考え方】
内接円の半径を求める方法は、式を使うなら「三角形の面積」に着目する方法が使えます。2通りで書いて、内接円の半径を計算していきます。
辺の長さをいじっていくのは難しいので、正弦定理をつかって三角関数に変換して考えたほうがいいでしょう。ただし、計算はかなり大変です。式変形だけで最後までたどり着くのはなかなか難しいです。
別解としては、一部分を図形的に解く方法があります。まず、内接円の半径が最大になるには、少なくとも二等辺三角形でないといけないこと、さらに、その中でも正三角形でないといけないことを示していきます。計算は必要ですが、「二等辺三角形のとき」であることがわかるだけでも、計算量はグッと減ります。
シンプルな問題文ですが、難易度はこの年で一番難しいです。
解答編
【問題】
平面上の点Oを中心とし半径1の円周上に相異なる3点A,B,Cがある。$\triangle \mathrm{ ABC }$の内接円の半径rは$\displaystyle \frac{1}{2}$以下であることを示せ。
【解答】
$\triangle \mathrm{ ABC }$の面積Sは
\begin{eqnarray}
S
&=&
\frac{1}{2}\mathrm{ AB } \cdot \mathrm{ BC } \sin \mathrm{ B } \\[5pt]
\end{eqnarray}であり、正弦定理より
\begin{eqnarray}
S
&=&
\frac{1}{2} \cdot 2 \sin \mathrm{ C } \cdot 2 \sin \mathrm{ A } \cdot \sin \mathrm{ B } \\[5pt]
&=&
2 \sin \mathrm{ A } \sin \mathrm{ B } \sin \mathrm{ C } \\[5pt]
\end{eqnarray}となる。
また、内接円の半径rを使って書くと、面積Sは次のようにも書ける。
\begin{eqnarray}
S
&=&
\frac{1}{2}r(\mathrm{ AB }+\mathrm{ BC }+\mathrm{ CA }) \\[5pt]
&=&
r(\sin \mathrm{ A } +\sin \mathrm{ B } +\sin \mathrm{ C }) \\[5pt]
\end{eqnarray}
よって、内接円の半径rは次のように書ける。
\begin{eqnarray}
r
&=&
\frac{ 2\sin \mathrm{ A }\sin \mathrm{ B }\sin \mathrm{ C } }{ \sin \mathrm{ A } +\sin \mathrm{ B } +\sin \mathrm{ C } } \\[5pt]
&=&
\frac{ 2\sin \mathrm{ A }\sin \mathrm{ B }\sin (\mathrm{ A+B }) }{ \sin \mathrm{ A } +\sin \mathrm{ B } +\sin (\mathrm{ A+B }) } \\[5pt]
\end{eqnarray}ここで、和積の公式と倍角の公式を使うと
\begin{eqnarray}
r
&=&
\frac{ 2\sin \mathrm{ A }\sin \mathrm{ B }\cdot 2\sin\frac{\mathrm{ A+B } }{2} \cos\frac{\mathrm{ A+B } }{2} }{ 2\sin\frac{\mathrm{ A+B } }{2} \cos\frac{\mathrm{ A-B } }{2} +2\sin\frac{\mathrm{ A+B } }{2} \cos\frac{\mathrm{ A+B } }{2} } \\[5pt]
&=&
\frac{ 2\sin \mathrm{ A } \sin \mathrm{ B } \cos\frac{\mathrm{ A+B } }{2} }{ \cos\frac{\mathrm{ A-B } }{2} +\cos\frac{\mathrm{ A+B } }{2} } \\[5pt]
\end{eqnarray}となる。さらに和積の公式と倍角の公式を使うと
\begin{eqnarray}
r
&=&
\frac{ 2 \cdot 2\sin\frac{\mathrm{ A } }{2}\cos\frac{\mathrm{ A } }{2} \cdot 2\sin\frac{\mathrm{ B } }{2}\cos\frac{\mathrm{ B } }{2} \cos\frac{\mathrm{ A+B } }{2} }{ 2\cos\frac{\mathrm{ A } }{2} \cos\frac{\mathrm{ B } }{2} } \\[5pt]
&=&
4 \sin\frac{\mathrm{ A } }{2} \sin\frac{\mathrm{ B } }{2}\cos\frac{\mathrm{ A+B } }{2} \\[5pt]
\end{eqnarray}となる。
ここで、積和の公式を使えば
\begin{eqnarray}
r
&=&
4 \sin\frac{\mathrm{ A } }{2} \sin\frac{\mathrm{ B } }{2}\cos\frac{\mathrm{ A+B } }{2} \\[5pt]
&=&
4 \cdot \frac{-1}{2} \left(\cos\frac{\mathrm{ A+B } }{2} -\cos\frac{\mathrm{ A-B } }{2} \right) \cos\frac{\mathrm{ A+B } }{2} \\[5pt]
&=&
-2 \cos^2\frac{\mathrm{ A+B } }{2} +2\cos\frac{\mathrm{ A+B } }{2}\cos\frac{\mathrm{ A-B } }{2} \\[5pt]
\end{eqnarray}となる。ここで、$\cos\frac{\mathrm{ A+B } }{2} \gt 0$だから、
\begin{eqnarray}
r
&\leqq&
-2 \cos^2\frac{\mathrm{ A+B } }{2} +2\cos\frac{\mathrm{ A+B } }{2} \cdot 1 \\[5pt]
&=&
-2 \left( \cos\frac{\mathrm{ A+B } }{2} -\frac{1}{2} \right)^2 +\frac{1}{2} \\[5pt]
&\leqq&
\frac{1}{2}
\end{eqnarray}となる。よって、内接円の半径rは$\displaystyle \frac{1}{2}$以下となる。
【解答終】
【解説】
最大になるのは、後半の式変形からわかる通り、$\cos\frac{\mathrm{ A-B } }{2}=1$、かつ、$\cos\frac{\mathrm{ A+B } }{2} = \frac{1}{2}$のときです。1つ目から二等辺三角形であることがわかるので、2つ目もあわせると、内接円の半径が最大になるのは正三角形のときであることがわかります。
なお、$\cos\frac{\mathrm{ A+B } }{2}$というのは、$\sin\frac{\mathrm{ C } }{2}$のことです。なので、内接円の半径rは次のようなきれいな式で書くことができます。\[ r = 4 \sin\frac{\mathrm{ A } }{2} \sin\frac{\mathrm{ B } }{2} \sin\frac{\mathrm{ C } }{2} \]
また、これは高度なテクニックですが、相加相乗平均を3つの場合に使うと
\[ \sin\frac{\mathrm{ A } }{2} \sin\frac{\mathrm{ B } }{2} \sin\frac{\mathrm{ C } }{2} \leqq \left( \frac{ \sin\frac{\mathrm{ A } }{2} +\sin\frac{\mathrm{ B } }{2} +\sin\frac{\mathrm{ C } }{2} }{3} \right)^3 \]となります。また、上に凸な関数$f(x)$に対して、$\lambda_1,\lambda_2,\lambda_3\geqq 0$で$\lambda_1+\lambda_2+\lambda_3=1$のとき、\[\lambda_1f(x_1)+\lambda_2f(x_2)+\lambda_3f(x_3) \leqq f(\lambda_1x_1+\lambda_2x_2+\lambda_3x_3)\]が成り立つので、
\begin{eqnarray}
& &
\left( \frac{ \sin\frac{\mathrm{ A } }{2} +\sin\frac{\mathrm{ B } }{2} +\sin\frac{\mathrm{ C } }{2} }{3} \right)^3 \\[5pt]
&\leqq&
\left( \sin \frac{\frac{\mathrm{ A } }{2}+\frac{\mathrm{ B } }{2}+\frac{\mathrm{ C } }{2} }{3} \right)^3 \\[5pt]
&=&
\left( \sin \frac{\mathrm{ A }+\mathrm{ B }+\mathrm{ C } }{6} \right)^3 \\[5pt]
&=&
\left( \sin \frac{ \pi }{6} \right)^3 \\[5pt]
&=&
\frac{1}{8} \\[5pt]
\end{eqnarray}となることがわかります。よって、$\displaystyle r=4 \sin\frac{\mathrm{ A } }{2} \sin\frac{\mathrm{ B } }{2} \sin\frac{\mathrm{ C } }{2} \leqq \frac{1}{2}$となることがわかります。これを試験中に使える人は少ないと思いますが。
続いての別解では、図形的に考えて少しだけ計算を楽にする方法で解いてみます。
別解編
【問題】
平面上の点Oを中心とし半径1の円周上に相異なる3点A,B,Cがある。$\triangle \mathrm{ ABC }$の内接円の半径rは$\displaystyle \frac{1}{2}$以下であることを示せ。
【別解】
半径1の円に内接する三角形に対し、内接円の半径が最大になるときを考える。
三角形ABCの内接円の中心をOとする。まず、ABを固定したとき、内接円の半径が最大になるのが$\mathrm{ AC }=\mathrm{ BC }$のときであることを示す。
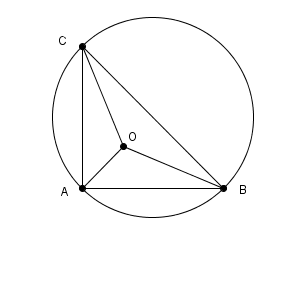
\begin{eqnarray}
\angle \mathrm{ AOB }
&=&
\pi -\angle \mathrm{ OAB } -\angle \mathrm{ OBA } \\[5pt]
&=&
\pi -\frac{\angle \mathrm{ CAB } +\angle \mathrm{ CBA } }{2} \\[5pt]
&=&
\pi -\frac{\pi -\angle \mathrm{ ACB } }{2} \\[5pt]
&=&
\frac{\pi +\angle \mathrm{ ACB } }{2}
\end{eqnarray}なので、点Cを弧AB上をAからBに移動させたとき、$\angle \mathrm{ AOB }$は一定だから、点OはA,Bを通るある円の円周上を動く。
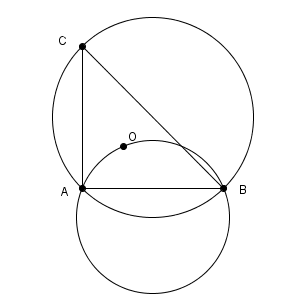
三角形ABCの内接円の半径は、OとABとの距離だから、最大になるのは三角形OABが$\mathrm{ OA }=\mathrm{ OB }$の二等辺三角形のとき。つまり、三角形ABCが$\mathrm{ AC }=\mathrm{ BC }$の二等辺三角形のときであることがわかる。
以上から、内接円の半径が最大になるのは、三角形ABCが二等辺三角形になるときであることがわかる。
次に、半径1の円に内接する二等辺三角形に対し、内接円の半径が最大になるときを考える。
$\mathrm{ AC }=\mathrm{ BC }$とする。また、ABの中点をDとし、$\angle \mathrm{ OAD }=\theta$とする。ここで、内接円の半径は$\mathrm{ OD }$である。
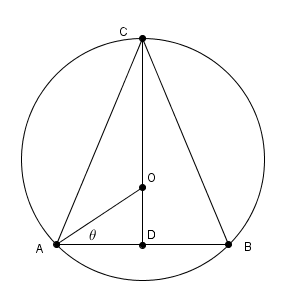
このとき、$\angle \mathrm{ ACB }=\pi-4\theta$であり、正弦定理から$\mathrm{ AB }=2\sin(\pi-4\theta)$である。よって、$\mathrm{ AD }=\sin(\pi-4\theta)$となる。以上から
\begin{eqnarray}
r
&=&
\mathrm{ OD } \\
&=&
\mathrm{ AD } \tan\angle\mathrm{ OAD } \\
&=&
\sin(\pi-4\theta) \tan\theta \\
&=&
\sin 4\theta \tan\theta \\
&=&
2\sin 2\theta \cos 2\theta \tan\theta \\
&=&
2\cdot 2\sin\theta\cos\theta (1-2\sin^2\theta) \frac{\sin\theta}{\cos\theta} \\[5pt]
&=&
4\sin^2\theta(1-2\sin^2\theta) \\[5pt]
&=&
-8\sin^4\theta +4\sin^2\theta \\[5pt]
&=&
-8\left(\sin^2\theta -\frac{1}{4}\right)^2 +\frac{1}{2} \\[5pt]
&\leqq&
\frac{1}{2} \\[5pt]
\end{eqnarray}が得られる。
以上より、三角形ABCの内接円の半径は$\displaystyle \frac{1}{2}$以下である。
【別解終】
【解説】
ちなみに、内接円の半径が最大になるのは、最後の式変形から$\sin\theta=\frac{1}{2}$のとき、つまり、正三角形のときであることが、この解法でも確認することができますね。





