センター試験 数学II・数学B 2020年度 第4問 解説
【選択問題】(第3問~第5問から2問選択)
問題編
問題
点 $\mathrm{O}$ を原点とする座標空間に2点 $\mathrm{A}(3,3,-6)$, $\mathrm{B}(2+2\sqrt{3},2-2\sqrt{3},-4)$ をとる。3点 $\mathrm{O, A, B}$ の定める平面を $\alpha$ とする。また、 $\alpha$ に含まれる点 $\mathrm{C}$ は\[ \overrightarrow{ \mathrm{ OA } }\perp \overrightarrow{ \mathrm{ OC } }, \quad \overrightarrow{ \mathrm{ OB } }\cdot \overrightarrow{ \mathrm{ OC } }=24 \quad \cdots ①\]を満たすとする。
(1) $|\overrightarrow{\mathrm{OA} }|=\myBox{ア}\sqrt{\myBox{イ} }$, $|\overrightarrow{\mathrm{OB} }|=\myBox{ウ}\sqrt{\myBox{エ} }$ であり、 $\overrightarrow{\mathrm{OA} }\cdot\overrightarrow{\mathrm{OB} }=\myBox{オカ}$ である。
(2) 点 $\mathrm{C}$ は平面 $\alpha$ 上にあるので、実数 $s,t$ を用いて、 $\overrightarrow{\mathrm{OC} }=s\overrightarrow{\mathrm{OA} }+t\overrightarrow{\mathrm{OB} }$ と表すことができる。このとき、①から $s=\dfrac{\myBox{キク} }{\myBox{ケ} }$, $t=\myBox{コ}$ である。したがって、 $|\overrightarrow{\mathrm{OC} }|=\myBox{サ}\sqrt{\myBox{シ} }$ である。
(3) $\overrightarrow{\mathrm{CB} }=\left(\myBox{ス},\myBox{セ},\myBox{ソタ}\right)$ である。したがって、平面 $\alpha$ 上の四角形 $\mathrm{OABC}$ は $\myBox{チ}$ 。 $\myBox{チ}$ に当てはまるものを、次の 0 ~ 4 のうちから一つ選べ。ただし、少なくとも一組の対辺が平行な四角形を台形という。
0: 正方形である
1: 正方形ではないが、長方形である
2: 長方形ではないが、平行四辺形である
3: 平行四辺形ではないが、台形である
4: 台形ではない
$\overrightarrow{\mathrm{OA} }\perp\overrightarrow{\mathrm{OC} }$ であるので、四角形 $\mathrm{OABC}$ の面積は $\myBox{ツテ}$ である。
(4) $\overrightarrow{\mathrm{OA} }\perp\overrightarrow{\mathrm{OD} }$, $\overrightarrow{\mathrm{OC} }\cdot\overrightarrow{\mathrm{OD} }=2\sqrt{6}$ かつ $z$ 座標が $1$ であるような点 $\mathrm{D}$ の座標は\[\left(\myBox{ト}+\dfrac{\sqrt{\myBox{ナ} }}{\myBox{ニ} }, \myBox{ヌ}-\dfrac{\sqrt{\myBox{ネ} }}{\myBox{ノ} },1\right)\]である。このとき $\angle \mathrm{COD}=\myBox{ハヒ}^{\circ}$ である。
3点 $\mathrm{O,C,D}$ の定める平面を $\beta$ とする。 $\alpha$ と $\beta$ は垂直であるので、三角形 $\mathrm{ABC}$ を底面とする四面体 $\mathrm{DABC}$ の高さは $\sqrt{\myBox{フ} }$ である。したがって、四面体 $\mathrm{DABC}$ の体積は $\myBox{ヘ}\sqrt{\myBox{ホ} }$ である。
考え方
(1)は、基本的な内積の計算です。(2)も、どの条件式を使うのかが指定されているので、内積の計算をしていきます。
(3)は見慣れない形式ですが、各辺をベクトルで表すと、答えを特定することができます。
(4)は四面体の体積を求めますが、高さをどう求めるかがネックです。空間なので考えづらいですが、今まで求めたものをヒントにして考えていきます。
【選択問題】(第3問~第5問から2問選択)
解答編
問題
点 $\mathrm{O}$ を原点とする座標空間に2点 $\mathrm{A}(3,3,-6)$, $\mathrm{B}(2+2\sqrt{3},2-2\sqrt{3},-4)$ をとる。3点 $\mathrm{O, A, B}$ の定める平面を $\alpha$ とする。また、 $\alpha$ に含まれる点 $\mathrm{C}$ は\[ \overrightarrow{ \mathrm{ OA } }\perp \overrightarrow{ \mathrm{ OC } }, \quad \overrightarrow{ \mathrm{ OB } }\cdot \overrightarrow{ \mathrm{ OC } }=24 \quad \cdots ①\]を満たすとする。
(1) $|\overrightarrow{\mathrm{OA} }|=\myBox{ア}\sqrt{\myBox{イ} }$, $|\overrightarrow{\mathrm{OB} }|=\myBox{ウ}\sqrt{\myBox{エ} }$ であり、 $\overrightarrow{\mathrm{OA} }\cdot\overrightarrow{\mathrm{OB} }=\myBox{オカ}$ である。
解説
\begin{eqnarray} & & |\overrightarrow{\mathrm{OA} }|^2 \\[5pt] &=& 3^2+3^2+(-6)^2 \\[5pt] &=& 9+9+36 \\[5pt] &=& 54 \\[5pt] \end{eqnarray}なので、 $|\overrightarrow{\mathrm{OA} }|=3\sqrt{6}$ です。 \begin{eqnarray} & & |\overrightarrow{\mathrm{OB} }|^2 \\[5pt] &=& (2+2\sqrt{3})^2+(2-2\sqrt{3})^2+(-4)^2 \\[5pt] &=& (4+8\sqrt{3}+12)\\ & &+(4-8\sqrt{3}+12)+16 \\[5pt] &=& 48 \\[5pt] \end{eqnarray}なので、 $|\overrightarrow{\mathrm{OB} }|=4\sqrt{3}$ です。また、
\begin{eqnarray}
& &
\overrightarrow{\mathrm{OA} }\cdot\overrightarrow{\mathrm{OB} } \\[5pt]
&=&
3(2+2\sqrt{3}) +3(2-2\sqrt{3})+(-6)\cdot(-4) \\[5pt]
&=&
6 +6+24 \\[5pt]
&=&
36 \\[5pt]
\end{eqnarray}となります。
解答
アイ:36
ウエ:43
オカ:36
解答編 つづき
問題
(2) 点 $\mathrm{C}$ は平面 $\alpha$ 上にあるので、実数 $s,t$ を用いて、 $\overrightarrow{\mathrm{OC} }=s\overrightarrow{\mathrm{OA} }+t\overrightarrow{\mathrm{OB} }$ と表すことができる。このとき、①から $s=\dfrac{\myBox{キク} }{\myBox{ケ} }$, $t=\myBox{コ}$ である。したがって、 $|\overrightarrow{\mathrm{OC} }|=\myBox{サ}\sqrt{\myBox{シ} }$ である。
解説
$\overrightarrow{ \mathrm{ OA } }\perp \overrightarrow{ \mathrm{ OC } }$ より、内積は $0$ だから、
\begin{eqnarray}
\overrightarrow{ \mathrm{ OA } }\cdot \overrightarrow{ \mathrm{ OC } } &=& 0 \\[5pt]
\overrightarrow{ \mathrm{ OA } }\cdot (s\overrightarrow{\mathrm{OA} }+t\overrightarrow{\mathrm{OB} }) &=& 0 \\[5pt]
s|\overrightarrow{ \mathrm{ OA } }|^2 +t \overrightarrow{\mathrm{OA} }\cdot \overrightarrow{\mathrm{OB} } &=& 0 \\[5pt]
54s+36t &=& 0 \\[5pt]
3s+2t &=& 0 \\[5pt]
\end{eqnarray}が得られます。
また、 $\overrightarrow{ \mathrm{ OB } }\cdot \overrightarrow{ \mathrm{ OC } }=24$ より
\begin{eqnarray}
\overrightarrow{ \mathrm{ OB } }\cdot (s\overrightarrow{\mathrm{OA} }+t\overrightarrow{\mathrm{OB} }) &=& 24 \\[5pt]
s\overrightarrow{\mathrm{OA} }\cdot \overrightarrow{\mathrm{OB} } +t|\overrightarrow{ \mathrm{ OB } }|^2 &=& 24 \\[5pt]
36s+48t &=& 24 \\[5pt]
3s+4t &=& 2 \\[5pt]
\end{eqnarray}が得られます。
2つの式を辺々引くと、 $-2t=-2$ より、 $t=1$ となり、 $s=-\dfrac{2t}{3}=\dfrac{-2}{3}$ となることがわかります。
$\overrightarrow{\mathrm{OC} }=-\dfrac{2}{3}\overrightarrow{\mathrm{OA} }+\overrightarrow{\mathrm{OB} }$ と書けることがわかったので、
\begin{eqnarray} & & |\overrightarrow{\mathrm{OC} }|^2 \\[5pt] &=& \dfrac{4}{9}|\overrightarrow{\mathrm{OA} }|^2 -\dfrac{4}{3}\overrightarrow{\mathrm{OA} }\cdot\overrightarrow{\mathrm{OB} }+|\overrightarrow{\mathrm{OB} }|^2 \\[5pt] &=& \dfrac{4}{9}\cdot 54 -\dfrac{4}{3} \cdot 36+48 \\[5pt] &=& 24 -48+48 \\[5pt] &=& 24 \end{eqnarray}なので、 $|\overrightarrow{\mathrm{OC} }|=2\sqrt{6}$ です。解答
キクケ:-23
コ:1
サシ:26
解答編 つづき
問題
(3) $\overrightarrow{\mathrm{CB} }=\left(\myBox{ス},\myBox{セ},\myBox{ソタ}\right)$ である。したがって、平面 $\alpha$ 上の四角形 $\mathrm{OABC}$ は $\myBox{チ}$ 。 $\myBox{チ}$ に当てはまるものを、次の 0 ~ 4 のうちから一つ選べ。ただし、少なくとも一組の対辺が平行な四角形を台形という。
0: 正方形である
1: 正方形ではないが、長方形である
2: 長方形ではないが、平行四辺形である
3: 平行四辺形ではないが、台形である
4: 台形ではない
$\overrightarrow{\mathrm{OA} }\perp\overrightarrow{\mathrm{OC} }$ であるので、四角形 $\mathrm{OABC}$ の面積は $\myBox{ツテ}$ である。
解説
\begin{eqnarray} & & \overrightarrow{\mathrm{CB} } \\[5pt] &=& \overrightarrow{\mathrm{OB} }-\overrightarrow{\mathrm{OC} } \\[5pt] &=& \overrightarrow{\mathrm{OB} }-\left(-\dfrac{2}{3}\overrightarrow{\mathrm{OA} }+\overrightarrow{\mathrm{OB} }\right) \\[5pt] &=& \dfrac{2}{3}\overrightarrow{\mathrm{OA} } \\[5pt] &=& (2,2,-4) \\[5pt] \end{eqnarray}となります。上の計算から、 $\overrightarrow{\mathrm{CB} }=\dfrac{2}{3}\overrightarrow{\mathrm{OA} }$ は $\overrightarrow{\mathrm{OA} }$ と平行で、長さが異なるので、四角形 $\mathrm{OABC}$ は平行四辺形ではないが、台形であることがわかります。
四角形の部分だけを抜き出すと、次のようになります。
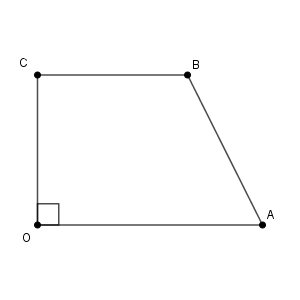
$\mathrm{OA}=3\sqrt{6}$, $\mathrm{CB}=\dfrac{2}{3}\mathrm{OA}=2\sqrt{6}$, $\mathrm{OC}=2\sqrt{6}$ なので、台形の面積は\[ (3\sqrt{6}+2\sqrt{6})\cdot 2\sqrt{6}\cdot\dfrac{1}{2}=30 \]となります。
解答
スセソタ:22-4
チ:3
ツテ:30
解答編 つづき
問題
(4) $\overrightarrow{\mathrm{OA} }\perp\overrightarrow{\mathrm{OD} }$, $\overrightarrow{\mathrm{OC} }\cdot\overrightarrow{\mathrm{OD} }=2\sqrt{6}$ かつ $z$ 座標が $1$ であるような点 $\mathrm{D}$ の座標は\[\left(\myBox{ト}+\dfrac{\sqrt{\myBox{ナ} }}{\myBox{ニ} }, \myBox{ヌ}-\dfrac{\sqrt{\myBox{ネ} }}{\myBox{ノ} },1\right)\]である。このとき $\angle \mathrm{COD}=\myBox{ハヒ}^{\circ}$ である。
解説
$\mathrm{D}$ の座標を $(x,y,1)$ とすると、 $\overrightarrow{\mathrm{OA} }\perp\overrightarrow{\mathrm{OD} }$ より内積が $0$ だから、
\begin{eqnarray}
\overrightarrow{ \mathrm{ OA } }\cdot \overrightarrow{ \mathrm{ OD } } &=& 0 \\[5pt]
(3,3,-6)\cdot (x,y,1) &=& 0 \\[5pt]
3x+3y-6 &=& 0 \\[5pt]
x+y &=& 2 \\[5pt]
\end{eqnarray}が得られます。
また、 $\overrightarrow{\mathrm{OC} }\cdot\overrightarrow{\mathrm{OD} }=2\sqrt{6}$ より
\begin{eqnarray}
\overrightarrow{ \mathrm{ OC } }\cdot \overrightarrow{ \mathrm{ OD } } &=& 2\sqrt{6} \\[5pt]
-\dfrac{2}{3}\overrightarrow{ \mathrm{ OA } }\cdot \overrightarrow{ \mathrm{ OD } }+\overrightarrow{ \mathrm{ OB } }\cdot \overrightarrow{ \mathrm{ OD } } &=& 2\sqrt{6} \\[5pt]
\end{eqnarray}となりますが、 $\overrightarrow{\mathrm{OA} }\perp\overrightarrow{\mathrm{OD} }$ より前半は $0$ なので、
\begin{eqnarray}
(2+2\sqrt{3},2-2\sqrt{3},-4)\cdot (x,y,1) &=& 2\sqrt{6} \\[5pt]
(2+2\sqrt{3})x+(2-2\sqrt{3})y-4 &=& 2\sqrt{6} \\[5pt]
\end{eqnarray}となります。先ほどの $x+y=2$ であることを使うと
\begin{eqnarray}
2\sqrt{3}x-2\sqrt{3}y &=& 2\sqrt{6} \\[5pt]
x-y &=& \sqrt{2} \\[5pt]
\end{eqnarray}が得られます。
辺々足すと $2x=2+\sqrt{2}$ から $x=1+\dfrac{\sqrt{2} }{2}$ が得られ、これを代入すると $y=1-\dfrac{\sqrt{2} }{2}$ となります。
\begin{eqnarray} & & |\overrightarrow{\mathrm{OD} }|^2 \\[5pt] &=& \left(1+\dfrac{\sqrt{2} }{2}\right)^2+\left(1-\dfrac{\sqrt{2} }{2}\right)^2+1^2 \\[5pt] &=& 1+\sqrt{2}+\dfrac{1}{2} +1-\sqrt{2}+\dfrac{1}{2} +1 \\[5pt] &=& 4 \\[5pt] \end{eqnarray}なので、 $|\overrightarrow{\mathrm{OD} }|=2$ だから、 \begin{eqnarray} \overrightarrow{\mathrm{OC} }\cdot\overrightarrow{\mathrm{OD} } &=& 2\sqrt{6} \\[5pt] |\overrightarrow{\mathrm{OC} }||\overrightarrow{\mathrm{OD} }|\cos\angle \mathrm{COD} &=& 2\sqrt{6} \\[5pt] 2\sqrt{6} \cdot 2 \cos\angle \mathrm{COD} &=& 2\sqrt{6} \\[5pt] \cos\angle \mathrm{COD} &=& \dfrac{1}{2} \\[5pt] \end{eqnarray}なので、 $\angle \mathrm{COD}=60^{\circ}$ となります。解答
トナニ:122
ヌネノ:122
ハヒ:60
解答編 つづき
問題
3点 $\mathrm{O,C,D}$ の定める平面を $\beta$ とする。 $\alpha$ と $\beta$ は垂直であるので、三角形 $\mathrm{ABC}$ を底面とする四面体 $\mathrm{DABC}$ の高さは $\sqrt{\myBox{フ} }$ である。したがって、四面体 $\mathrm{DABC}$ の体積は $\myBox{ヘ}\sqrt{\myBox{ホ} }$ である。
解説
$\mathrm{OA}$ は $\mathrm{OC}$, $\mathrm{OD}$ のどちらにも垂直なので、 $\mathrm{OA}$ は平面 $\beta$ と垂直であり、平面 $\alpha$ と $\beta$ も垂直になります。
三角形 $\mathrm{ABC}$ を底面と考えたとき、四面体 $\mathrm{DABC}$ の高さは、点 $\mathrm{D}$ から平面 $\alpha$ に下した垂線の長さになります。2つの平面のうち、必要な部分を抜き出してかくと、次のようになります。
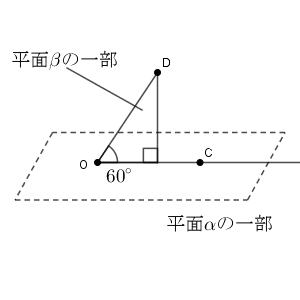
平面 $\alpha$ と $\beta$ は垂直であり、 $\mathrm{O, C}$ は平面 $\alpha,\beta$ のどちらの平面にもある点だから、平面 $\beta$ 上の点 $\mathrm{D}$ から平面 $\alpha$ におろした垂線の足は、直線 $\mathrm{OC}$ 上にあります。 $\angle \mathrm{COD}=60^{\circ}$ なので、高さは\[ |\overrightarrow{\mathrm{OD} }|\sin60^{\circ}=\sqrt{3} \]となります。
三角形 $\mathrm{ABC}$ の面積は、台形の面積を求めたときの図を利用して\[ \dfrac{2\sqrt{6}\cdot 2\sqrt{6} }{2}=12 \]と求められるので、四面体 $\mathrm{DABC}$ の体積は\[ \dfrac{12\cdot\sqrt{3} }{3}=4\sqrt{3} \]となります。
解答
フヘホ:343





