センター試験 数学II・数学B 2020年度 第1問 [2] 解説
【必答問題】
問題編
問題
(1) $t$ は正の実数であり、 $t^{\frac{1}{3} }-t^{-\frac{1}{3} }=-3$ を満たすとする。このとき\[ t^{\frac{2}{3} }+t^{-\frac{2}{3} }=\myBox{タチ} \]である。さらに\[ t^{\frac{1}{3} }+t^{-\frac{1}{3} }=\sqrt{\myBox{ツテ} }, \ t-t^{-1}=\myBox{トナニ} \]である。
(2) $x,y$ は正の実数とする。連立不等式
\begin{eqnarray} \left\{ \begin{array}{l} \log_3 (x\sqrt{y}) \leqq 5 \quad \cdots ② \\ \log_{81} \dfrac{y}{x^3} \leqq 1 \quad \cdots ③ \\ \end{array} \right. \end{eqnarray}について考える。$X=\log_3 x$, $Y=\log_3 y$ とおくと、②は\[ \myBox{ヌ}X+Y\leqq\myBox{ネノ} \quad \cdots ④ \]と変形でき、③は\[ \myBox{ハ}X-Y\geqq\myBox{ヒフ} \quad \cdots ⑤ \]と変形できる。
$X, Y$ が④と⑤を満たすとき、 $Y$ のとり得る最大の整数の値は $\myBox{ヘ}$ である。また、 $x,y$ が②, ③と $\log_3y=\mybox{ヘ}$ を同時に満たすとき、 $x$ のとり得る最大の整数の値は $\myBox{ホ}$ である。
考え方
(1)は、式の値を求める、よくある計算です。
(2)は、前半は、対数の基本的な計算です。後半は、領域をかいて考えましょう。 $X, Y$ を考えているのか、 $x,y$ を考えているのか、混乱しないようにしましょう。
【必答問題】
解答編
問題
(1) $t$ は正の実数であり、 $t^{\frac{1}{3} }-t^{-\frac{1}{3} }=-3$ を満たすとする。このとき\[ t^{\frac{2}{3} }+t^{-\frac{2}{3} }=\myBox{タチ} \]である。さらに\[ t^{\frac{1}{3} }+t^{-\frac{1}{3} }=\sqrt{\myBox{ツテ} }, \ t-t^{-1}=\myBox{トナニ} \]である。
解説
$t^{\frac{1}{3} }-t^{-\frac{1}{3} }=-3$ なので、両辺を2乗して
\begin{eqnarray}
t^{\frac{2}{3} }-2+t^{-\frac{2}{3} } &=& 9 \\[5pt]
t^{\frac{2}{3} }+t^{-\frac{2}{3} } &=& 11 \\[5pt]
\end{eqnarray}と求められます。
また、
\begin{eqnarray}
& &
(t^{\frac{1}{3} }+t^{-\frac{1}{3} })^2 \\[5pt]
&=&
t^{\frac{2}{3} }+2+t^{-\frac{2}{3} } \\[5pt]
&=&
11+2=13
\end{eqnarray}となり、 $t^{\frac{1}{3} }+t^{-\frac{1}{3} }$ は正だから $\sqrt{13}$ となります。
\begin{eqnarray}
& &
t-t^{-1} \\[5pt]
&=&
(t^{\frac{1}{3} }-t^{-\frac{1}{3} }) (t^{\frac{2}{3} }+1-t^{-\frac{2}{3} }) \\[5pt]
&=&
-3 (11+1) \\[5pt]
&=&
-36
\end{eqnarray}と計算できます。
解答
タチ:11
ツテ:13
トナニ:-36
解答編 つづき
問題
(2) $x,y$ は正の実数とする。連立不等式
\begin{eqnarray} \left\{ \begin{array}{l} \log_3 (x\sqrt{y}) \leqq 5 \quad \cdots ② \\ \log_{81} \dfrac{y}{x^3} \leqq 1 \quad \cdots ③ \\ \end{array} \right. \end{eqnarray}について考える。$X=\log_3 x$, $Y=\log_3 y$ とおくと、②は\[ \myBox{ヌ}X+Y\leqq\myBox{ネノ} \quad \cdots ④ \]と変形でき、③は\[ \myBox{ハ}X-Y\geqq\myBox{ヒフ} \quad \cdots ⑤ \]と変形できる。
解説
②は
\begin{eqnarray}
\log_3 (x\sqrt{y}) & \leqq & 5\\[5pt]
\log_3 x +\dfrac{1}{2} \log_3 y & \leqq & 5 \\[5pt]
2\log_3 x +\log_3 y & \leqq & 10 \\[5pt]
2X +Y & \leqq & 10 \\[5pt]
\end{eqnarray}と変形できます。
③は
\begin{eqnarray}
\log_{81} \dfrac{y}{x^3} & \leqq & 1 \\[5pt]
\dfrac{\log_3 \dfrac{y}{x^3} }{\log_3 81} & \leqq & 1 \\[5pt]
\dfrac{\log_3 y -\log_3 x^3}{4} & \leqq & 1 \\[5pt]
\log_3 y -3\log_3 x & \leqq & 4 \\[5pt]
3X -Y & \geqq & -4 \\[5pt]
\end{eqnarray}と変形できます。
解答
ヌネノ:210
ハヒフ:3-4
解答編 つづき
問題
$X, Y$ が④と⑤を満たすとき、 $Y$ のとり得る最大の整数の値は $\myBox{ヘ}$ である。また、 $x,y$ が②, ③と $\log_3y=\mybox{ヘ}$ を同時に満たすとき、 $x$ のとり得る最大の整数の値は $\myBox{ホ}$ である。
解説
$Y$ は、 $Y\leqq -2X+10$ かつ $Y\leqq 3X+4$ を満たします。 $-2X+10=3X+4$ とすると $X=\dfrac{6}{5}$ であり、このときの両辺の値は $\dfrac{38}{5}$ となります。よって、この領域を図示すると、次の部分になります。
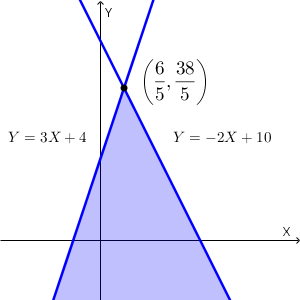
連立不等式を満たす $Y$ のうち、最大の整数は $7$ だとわかります。
$Y=7$ のとき、 $7\leqq -2X+10$ を解くと $X\leqq \dfrac{3}{2}$ であり、 $7\leqq 3X+4$ を解くと $X\geqq 1$ となります。よって、 $X$ のとりうる範囲は $1\leqq X \leqq \dfrac{3}{2}$ です。 $X=\log_3 x$ なので、 $3^1\leqq x \leqq 3^{\frac{3}{2} }=\sqrt{27}$ となることから、 $x$ のとり得る最大の整数は $5$ だとわかります。
解答
ヘホ:75





