センター試験 数学II・数学B 2019年度追試 第4問 解説
【選択問題】(第3問~第5問から2問選択)
問題編
問題
点 O を原点とする座標空間に3点 $\mathrm{ P }(0,6,3)$, $\mathrm{ Q }(4,-2,-5)$, $\mathrm{ R }(12,0,-3)$ がある。3点 O, P, Q の定める平面を $\alpha$ とし、 $\alpha$ 上で $\angle \mathrm{ POQ }$ の二等分線 $\ell$ を考える。 $\ell$ 上に点 A を、 $|\overrightarrow{ \mathrm{ OA } }|=9$ かつ $x$ 座標が正であるようにとる。また、 $\alpha$ 上に点 H を、 $\overrightarrow{ \mathrm{ HR } }\perp \overrightarrow{ \mathrm{ OP } }$, $\overrightarrow{ \mathrm{ HR } }\perp \overrightarrow{ \mathrm{ OQ } }$ であるようにとる。
(1) $|\overrightarrow{ \mathrm{ OP } }|=\myBox{ア}\sqrt{\myBox{イ} }$, $|\overrightarrow{ \mathrm{ OQ } }|=\myBox{ウ}\sqrt{\myBox{エ} }$ であるから、 A の座標は $\left(\myBox{オ},\ \myBox{カ},\ \myBox{キク}\right)$ であることがわかる。
(2) 点 H の座標と線分 HR の長さを求めよう。 $\overrightarrow{ \mathrm{ OP } }\perp \vec{n}$, $\overrightarrow{ \mathrm{ OQ } }\perp\vec{n}$ であるベクトル $\vec{n}=\left(2,\ \myBox{ケコ},\ \myBox{サ}\right)$ に対し、 $\overrightarrow{ \mathrm{ HR } }=k\vec{n}$ とおくと $\overrightarrow{ \mathrm{ OH } }=\overrightarrow{ \mathrm{ OR } }-k\vec{n}$ である。 $\overrightarrow{ \mathrm{ OH } }\cdot\vec{n}=\myBox{シ}$ であるから、 $k=\myBox{ス}$ である。したがって、 H の座標は $\left(\myBox{セ},\ \myBox{ソ},\ \myBox{タチ}\right)$ であり、 HR の長さは $\myBox{ツ}$ である。
(3) 平面 $\alpha$ 上で点 A を中心とする半径 $1$ の円 $C$ を考える。点 B が $C$ 上を動くとき、線分 RB の長さの最大値と、そのときの B の座標を求めよう。
A と H の間の距離は $\myBox{テ}$ である。よって、 RB の長さの最大値は $\sqrt{\myBox{トナ} }$ である。また、 RB の長さが最大となる B は $\overrightarrow{ \mathrm{ HB } }=\dfrac{\myBox{ニ} }{\myBox{ヌ} }\overrightarrow{ \mathrm{ HA } }$ を満たすから、求める B の座標は\[ \left( \dfrac{\myBox{ネノ} }{\myBox{ハ} }, \dfrac{\myBox{ヒフ} }{\mybox{ハ} }, \dfrac{\myBox{ヘホ} }{\mybox{ハ} } \right) \]である。
考え方
空間ベクトルで、しかも角の二等分線というのは、ハードそうな設定です。しかし、(1)の前半の計算であることに気づけば、それほど難しい状況ではないことがわかります。
(2)は、平面に垂直なベクトルについて考えます。これにより、点 R から平面 $\alpha$ までの距離がわかります。
(3)は、図がかきづらいので考えにくいですね。どういうときに RB が最大になるかを考えるには、正確な図をかけなくても大丈夫です。平面 $\alpha$ と点 R との位置関係から考えましょう。
【選択問題】(第3問~第5問から2問選択)
解答編
問題
点 O を原点とする座標空間に3点 $\mathrm{ P }(0,6,3)$, $\mathrm{ Q }(4,-2,-5)$, $\mathrm{ R }(12,0,-3)$ がある。3点 O, P, Q の定める平面を $\alpha$ とし、 $\alpha$ 上で $\angle \mathrm{ POQ }$ の二等分線 $\ell$ を考える。 $\ell$ 上に点 A を、 $|\overrightarrow{ \mathrm{ OA } }|=9$ かつ $x$ 座標が正であるようにとる。また、 $\alpha$ 上に点 H を、 $\overrightarrow{ \mathrm{ HR } }\perp \overrightarrow{ \mathrm{ OP } }$, $\overrightarrow{ \mathrm{ HR } }\perp \overrightarrow{ \mathrm{ OQ } }$ であるようにとる。
(1) $|\overrightarrow{ \mathrm{ OP } }|=\myBox{ア}\sqrt{\myBox{イ} }$, $|\overrightarrow{ \mathrm{ OQ } }|=\myBox{ウ}\sqrt{\myBox{エ} }$ であるから、 A の座標は $\left(\myBox{オ},\ \myBox{カ},\ \myBox{キク}\right)$ であることがわかる。
解説
\begin{eqnarray} |\overrightarrow{ \mathrm{ OP } }|^2 &=& 0^2+6^2+3^2 \\[5pt] &=& 45 \end{eqnarray}であり、 \begin{eqnarray} |\overrightarrow{ \mathrm{ OQ } }|^2 &=& 4^2+(-2)^2+(-5)^2 \\[5pt] &=& 45 \end{eqnarray}なので、 $|\overrightarrow{ \mathrm{ OP } }|=3\sqrt{5}$, $|\overrightarrow{ \mathrm{ OQ } }|^2=3\sqrt{5}$ と求められます。よって、三角形 OPQ は、 $\mathrm{ OP=OQ }$ の二等辺三角形なので、線分PQ の中点を M とすると、 $\angle \mathrm{ POQ }$ の二等分線 $\ell$ は、直線 OM と一致します。点 A は直線 $\ell$ 上の点なので、 実数 $a$ を使って、 $\overrightarrow{ \mathrm{ OA } }=a\overrightarrow{ \mathrm{ OM } }$ とかけます。M の座標は
\begin{eqnarray}
& &
\left(\dfrac{0+4}{2},\dfrac{6+(-2)}{2},\dfrac{3+(-5)}{2}\right) \\[5pt]
&=&
(2,2,-1)
\end{eqnarray}なので、 A の座標は $(2a,2a,-a)$ となります。また、 $|\overrightarrow{ \mathrm{ OA } }|^2=9^2=81$ なので
\begin{eqnarray}
(2a)^2+(2a)^2+(-a)^2 &=& 81 \\[5pt]
9a^2 &=& 81 \\[5pt]
a &=& \pm 3 \\[5pt]
\end{eqnarray}となります。点 A の $x$ 座標は正なので、 $a=3$ であり、点 A の座標は $(6,6,-3)$ となります。
解答
アイ:35
ウエ:35
オカキク:66-3
解答編 つづき
(2) 点 H の座標と線分 HR の長さを求めよう。 $\overrightarrow{ \mathrm{ OP } }\perp \vec{n}$, $\overrightarrow{ \mathrm{ OQ } }\perp\vec{n}$ であるベクトル $\vec{n}=\left(2,\ \myBox{ケコ},\ \myBox{サ}\right)$ に対し、 $\overrightarrow{ \mathrm{ HR } }=k\vec{n}$ とおくと $\overrightarrow{ \mathrm{ OH } }=\overrightarrow{ \mathrm{ OR } }-k\vec{n}$ である。 $\overrightarrow{ \mathrm{ OH } }\cdot\vec{n}=\myBox{シ}$ であるから、 $k=\myBox{ス}$ である。
解説
問題文にあるように、 $\overrightarrow{ \mathrm{ OP } }$, $\overrightarrow{ \mathrm{ OQ } }$ に垂直で、 $x$ 成分が $2$ であるベクトル $\vec{n}$ を考えます。この成分を $(2,y,z)$ とおくと、 $\overrightarrow{ \mathrm{ OP } }$ との内積が $0$ になることから
\begin{eqnarray}
(0,6,3)\cdot(2,y,z) &=& 0 \\[5pt]
6y+3z &=& 0 \\[5pt]
z &=& -2y \\[5pt]
\end{eqnarray}となります。また、 $\overrightarrow{ \mathrm{ OQ } }$ との内積も $0$ なので、
\begin{eqnarray}
(4,-2,-5)\cdot(2,y,z) &=& 0 \\[5pt]
8-2y-5z &=& 0 \\[5pt]
\end{eqnarray}となります。これに $z=-2y$ を代入すると
\begin{eqnarray}
8-2y-5(-2y) &=& 0 \\[5pt]
8y &=& -8 \\[5pt]
y &=& -1 \\[5pt]
\end{eqnarray}となり、 $z=-2y=2$ と求められます。
$\overrightarrow{ \mathrm{ OP } }$ と $\overrightarrow{ \mathrm{ OQ } }$ は平行ではないので、これらと垂直なベクトルは、すべて平行となります。なので、 $\overrightarrow{ \mathrm{ HR } }$ は $\vec{n}$ の定数倍となります。これを問題文のように、\[ \overrightarrow{ \mathrm{ HR } }=k\vec{n} \]とおけば、\[ \overrightarrow{ \mathrm{ OH } }=\overrightarrow{ \mathrm{ OR } }+\overrightarrow{ \mathrm{ RH } }=\overrightarrow{ \mathrm{ OR } }-k\vec{n} \]となります。
また、 $\vec{n}$ は平面 $\alpha$ に垂直であり、 O, H は平面 $\alpha$ 上の点であるから、 $\overrightarrow{ \mathrm{ OH } }\cdot \vec{n}=0$ です。これを成分で表すと
\begin{eqnarray}
\overrightarrow{ \mathrm{ OH } }\cdot \vec{n} &=& 0 \\[5pt]
(\overrightarrow{ \mathrm{ OR } }-k\vec{n})\cdot \vec{n} &=& 0 \\[5pt]
(12,0,-3)\cdot (2,-1, 2)-k|(2,-1, 2)|^2 &=& 0 \\[5pt]
24-6-k(4+1+4) &=& 0 \\[5pt]
18-9k &=& 0 \\[5pt]
k &=& 2 \\[5pt]
\end{eqnarray}と求められます。
解答
ケコサ:-12
シス:02
解答編 つづき
したがって、 H の座標は $\left(\myBox{セ},\ \myBox{ソ},\ \myBox{タチ}\right)$ であり、 HR の長さは $\myBox{ツ}$ である。
解説
$k=2$ なので
\begin{eqnarray}
\overrightarrow{ \mathrm{ OH } }
&=&
\overrightarrow{ \mathrm{ OR } }-2\vec{n} \\[5pt]
&=&
(12,0,-3)-2(2,-1,2) \\[5pt]
&=&
(12-4,0+2,-3-4) \\[5pt]
&=&
(8,2,-7) \\[5pt]
\end{eqnarray}だから、 H の座標は $(8,2,-7)$ となります。
$\overrightarrow{ \mathrm{ HR } }=2\vec{n}$ であり、
\begin{eqnarray}
|\vec{n}|^2
&=&
2^2+(-1)^2+2^2 \\[5pt]
&=&
9
\end{eqnarray}だから、
\begin{eqnarray}
|\overrightarrow{ \mathrm{ HR } }|
&=&
2|\vec{n}| \\[5pt]
&=&
2\sqrt{9} \\[5pt]
&=&
6
\end{eqnarray}となります。
解答
セソタチ:82-7
ツ:6
解答編 つづき
(3) 平面 $\alpha$ 上で点 A を中心とする半径 $1$ の円 $C$ を考える。点 B が $C$ 上を動くとき、線分 RB の長さの最大値と、そのときの B の座標を求めよう。
A と H の間の距離は $\myBox{テ}$ である。よって、 RB の長さの最大値は $\sqrt{\myBox{トナ} }$ である。また、 RB の長さが最大となる B は $\overrightarrow{ \mathrm{ HB } }=\dfrac{\myBox{ニ} }{\myBox{ヌ} }\overrightarrow{ \mathrm{ HA } }$ を満たすから、求める B の座標は\[ \left( \dfrac{\myBox{ネノ} }{\myBox{ハ} }, \dfrac{\myBox{ヒフ} }{\mybox{ハ} }, \dfrac{\myBox{ヘホ} }{\mybox{ハ} } \right) \]である。
解説
$\mathrm{ A }(6,6,-3)$, $\mathrm{ H }(8,2,-7)$ なので、
\begin{eqnarray}
\mathrm{ AH }^2
&=&
(8-6)^2+(2-6)^2+(-7+3)^2 \\[5pt]
&=&
4+16+16 \\[5pt]
&=&
36
\end{eqnarray}から、 $\mathrm{ AH }=6$ と求められます。
座標通りの図ではないですが、平面 $\alpha$ と A, B, H, R の位置関係を図で表すと、次のようになっています。平面 $\alpha$ を上から見ているイメージです。
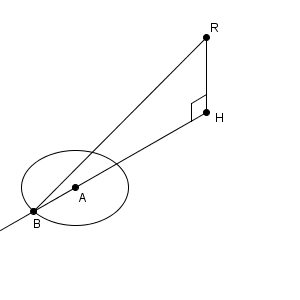
三角形BHR は直角三角形で、 RH の長さは一定なので、平面 $\alpha$ にある円上を点 B が動くとき、 BR が最大となるのは、 HB が最大のときです。そして、それは、 B, A, H がこの順に一直線上にあるときです。そのため、このときの RB の長さは
\begin{eqnarray}
& &
\sqrt{\mathrm{ RH }^2+(\mathrm{ AH }+\mathrm{ AB })^2} \\[5pt]
&=&
\sqrt{6^2+(6+1)^2} \\[5pt]
&=&
\sqrt{85} \\[5pt]
\end{eqnarray}となります。
このとき、 $\mathrm{ HB }$ の長さは $\mathrm{ HA }+1=6+1=7$ なので、\[ \overrightarrow{ \mathrm{ HB } }=\dfrac{7}{6}\overrightarrow{ \mathrm{ HA } } \]となるので、
\begin{eqnarray}
\overrightarrow{ \mathrm{ OB } }
&=&
\overrightarrow{ \mathrm{ OH } }+\overrightarrow{ \mathrm{ HB } } \\[5pt]
&=&
\overrightarrow{ \mathrm{ OH } }+\frac{7}{6}\overrightarrow{ \mathrm{ HA } } \\[5pt]
&=&
\overrightarrow{ \mathrm{ OH } }+\frac{7}{6}(\overrightarrow{ \mathrm{ OA } }-\overrightarrow{ \mathrm{ OH } }) \\[5pt]
&=&
-\frac{1}{6}\overrightarrow{ \mathrm{ OH } }+\frac{7}{6}\overrightarrow{ \mathrm{ OA } } \\[5pt]
&=&
-\frac{1}{6}(8,2,-7)+\frac{7}{6}(6,6,-3) \\[5pt]
&=&
\left(\frac{-8+42}{6},\frac{-2+42}{6},\frac{7-21}{6}\right) \\[5pt]
&=&
\left(\frac{34}{6},\frac{40}{6},\frac{-14}{6}\right) \\[5pt]
&=&
\left(\frac{17}{3},\frac{20}{3},\frac{-7}{3}\right) \\[5pt]
\end{eqnarray}となることから、 B の座標は\[ \left(\frac{17}{3},\frac{20}{3},\frac{-7}{3}\right) \]となります。
解答
テトナ:685
ニヌ:76
ネノハヒフヘホ:17320-7





