センター試験 数学II・数学B 2019年度追試 第2問 解説

【必答問題】

問題編

問題

　p, q, r を実数とし、 $p\gt 0$ とする。関数 $f(x)=px^3+qx$ は $x=1$ で極値をとるとする。曲線 $y=f(x)$ を $C$, 直線 $y=-x+r$ を $\ell$ とする。

(1) $f'(1)=\myBox{ア}$ であるから、 $q=\myBox{イウ}p$ である。また、点 $(s,f(s))$ における曲線 $C$ の接線は\[ y=\left(\myBox{エ}ps^2-\myBox{オ}p\right)x-\myBox{カ}ps^3 \quad \cdots ① \]と表せる。よって、 $C$ の接線の傾きは、 $s=\myBox{キ}$ のとき最小値 $\myBox{クケ}p$ をとる。

(2) 曲線 $C$ と直線 $y=-x$ の共有点の個数は、 $\mybox{クケ}p\geqq \myBox{コサ}$ のとき $\myBox{シ}$ 個で、 $\mybox{クケ}p \lt \mybox{コサ}$ のとき $\myBox{ス}$ 個となる。

　$C$ と直線 $\ell$ の共有点の個数が、 $r$ の値によらず $\myBox{セ}$ 個となるのは $0\lt p \leqq \dfrac{\myBox{ソ} }{\myBox{タ} }$ のときであり、 $p\gt \dfrac{\mybox{ソ} }{\mybox{タ} }$ のときは $C$ と $\ell$ の共有点の個数が、 $r$ の値によって1個、2個、および3個の場合がある。

(3) $p\gt \dfrac{\mybox{ソ} }{\mybox{タ} }$ とし、曲線 $C$ と直線 $\ell$ が3個の共有点をもつような $r$ の値の範囲を $p$ を用いて表そう。点 $(s,f(s))$ における $C$ の接線の傾きが $-1$ となるのは $s=\pm\sqrt{\dfrac{\myBox{チ}p-\myBox{ツ} }{\myBox{テ}p} }$ のときである。したがって、傾きが $-1$ となる $C$ の接線は2本あり、 $\ell$ がこれらの接線のどちらかに一致するとき、 $C$ と $\ell$ の共有点は、 $\myBox{ト}$ 個となる。①を用いて、これら2本の接線と y 軸との交点を求めれば、 $C$ と $\ell$ が3個の共有点をもつような $r$ の絶対値の範囲は\[ |r|\lt \frac{\myBox{ナ}p-\myBox{ニ} }{\myBox{ヌ} } \sqrt{\dfrac{\mybox{チ}p-\mybox{ツ} }{\mybox{テ}p} } \]であることがわかる。

(4) $u$ を $1$ 以上の実数とする。 $t$ が $t\gt u$ の範囲を動くとき、曲線 $y=x^2-1$ と $x$ 軸および2直線 $x=u$, $x=t$ で囲まれた図形の面積が $f(t)$ とつねに等しいとする。このとき、 $p=\dfrac{\myBox{ネ} }{\myBox{ノ} }$ であり、 $u=\sqrt{\myBox{ハ} }$ となる。

考え方

(1)は、極値や接線と微分との関係を考える問題です。

(2)は、式で考えてもグラフで考えても解けます。三次関数のほうがいろいろ動くので、グラフだと考えづらい人がいるかもしれません。三次関数のグラフがどうなるかに慣れていれば、直感的に答えがわかるでしょう。

(3)は、ごつそうな式が出てきますが、見た目ほど怖くはありません。誘導にしたがって計算していきましょう。

(4)は、面積を求める問題です。そのまま積分しても解けます。

【必答問題】

解答編

問題

　p, q, r を実数とし、 $p\gt 0$ とする。関数 $f(x)=px^3+qx$ は $x=1$ で極値をとるとする。曲線 $y=f(x)$ を $C$, 直線 $y=-x+r$ を $\ell$ とする。

(1) $f'(1)=\myBox{ア}$ であるから、 $q=\myBox{イウ}p$ である。

解説

$f(x)=px^3+qx$ が $x=1$ で極値をとることから、 $f'(1)=0$ となります。また、 $f'(x)=3px^2+q$ なので、
\begin{eqnarray} f'(1) &=& 0\\[5pt] 3p+q &=& 0\\[5pt] q &=& -3p\\[5pt] \end{eqnarray}となります。

解答

ア：0
イウ：-3

解答編 つづき

また、点 $(s,f(s))$ における曲線 $C$ の接線は\[ y=\left(\myBox{エ}ps^2-\myBox{オ}p\right)x-\myBox{カ}ps^3 \quad \cdots ① \]と表せる。よって、 $C$ の接線の傾きは、 $s=\myBox{キ}$ のとき最小値 $\myBox{クケ}p$ をとる。

解説

先ほどの結果から、$f(x)=px^3-3px$ とかけます。また、 $f'(x)=3px^2-3p$ なので、点 $(s,f(s))$ での接線の方程式は
\begin{eqnarray} y &=& f'(s)(x-s) +f(s) \\[5pt] &=& (3ps^2-3p)(x-s)+(ps^3-3ps) \\[5pt] &=& (3ps^2-3p)x-3ps^3+3ps+ps^3-3ps \\[5pt] &=& (3ps^2-3p)x-2ps^3 \\[5pt] \end{eqnarray}となります。

接線の傾きは $3p(s^2-1)$ なので、 $s$ を動かしたときにこれが最小になるのは $s=0$ のときであり、このときの接線の傾きは $-3p$ になることがわかります。

解答

エオカ：332
キ：0
クケ：-3

解答編 つづき

(2) 曲線 $C$ と直線 $y=-x$ の共有点の個数は、 $\mybox{クケ}p\geqq \myBox{コサ}$ のとき $\myBox{シ}$ 個で、 $\mybox{クケ}p \lt \mybox{コサ}$ のとき $\myBox{ス}$ 個となる。

解説

曲線 $C$: $y=px^3-3px$ と $y=-x$ の共有点の個数は、 $px^3-3px=-x$ の異なる実数解の個数と同じです。これは
\begin{eqnarray} px^3-3px &=& -x \\[5pt] x(px^2-3p+1) &=& 0 \\[5pt] \end{eqnarray}なので、まず $x=0$ が解であることがわかります。 $px^2-3p+1$ が $x=0$ 以外の実数解をもつのは、 $p\gt 0$ であることを考慮すると、 $-3p+1\lt 0$ のときだけであることがわかります。このとき、 実数解は合計で3個となります。

一方、 $-3p+1\geqq 0$ の場合は、実数解は $x=0$ だけの1個となります。

以上から、共有点の数は、 $-3p\geqq -1$ の場合は1個、 $-3p\lt -1$ の場合は3個となります。

また、図から考えることもできます。そもそも、 $(0,0)$ が共有点になることはすぐにわかります。解答欄を見ると、(1)の後半で求めた、 $x=0$ での接線の傾き $-3p$ を用いることがわかるので、これをヒントに $x=0$ での接線を考えてみます。

接線より $y=-x$ のほうが傾きが緩やかな場合、つまり、 $-3p\lt -1$ の場合は、共有点は3個になることがわかります。

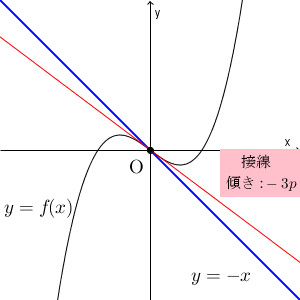
接線より $y=-x$ のほうが傾きが急な場合や、接線と $y=-x$ が一致する場合、つまり、 $-3p\geqq -1$ の場合は、共有点は1個になることがわかります。

解答

コサシス：-113

解答編 つづき

　$C$ と直線 $\ell$ の共有点の個数が、 $r$ の値によらず $\myBox{セ}$ 個となるのは $0\lt p \leqq \dfrac{\myBox{ソ} }{\myBox{タ} }$ のときであり、 $p\gt \dfrac{\mybox{ソ} }{\mybox{タ} }$ のときは $C$ と $\ell$ の共有点の個数が、 $r$ の値によって1個、2個、および3個の場合がある。

解説

曲線 $C$ と直線 $y=-x+r$ との共有点の個数は、\[ px^3-3px = -x+r \]の実数解の個数と一致します。つまり、\[ px^3+(-3p+1)x = r \]の実数解の個数と一致します。そのため、 $y=px^3+(-3p+1)x$ と $y=r$ との共有点の個数を考えればいいことがわかります。 $y=-x+r$ より $y=r$ の方が、直線が単純なので、共有点の数を考えやすくなります。

$g(x)=px^3+(-3p+1)x$ とすると、 $g'(x)=3px^2-3p+1$ となります。 $3px^2\geqq 0$ なので、 $-3p+1\geqq 0$ なら $g(x)$ は単調増加となります。そのため、 $y=r$ との共有点は次のようになります。

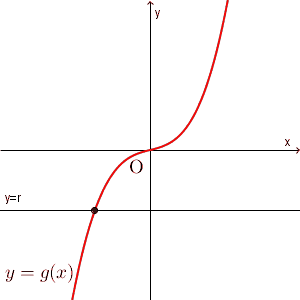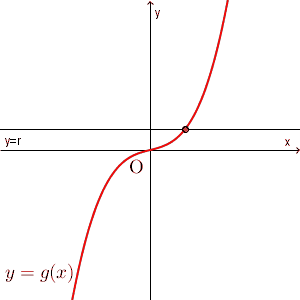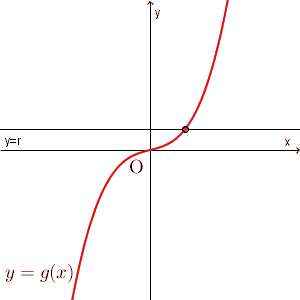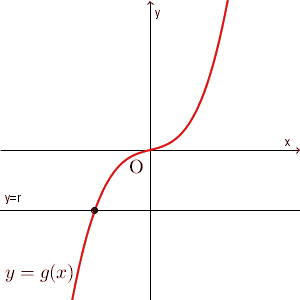
上のように、 $r$ の値が変わっても、共有点の数は1個です。

一方、 $-3p+1\lt 0$ の場合は、 $g'(x)=0$ となる $x$ が2つあり、 $y=g(x)$ のグラフは山と谷を含むものになります。よって、 $y=r$ との共有点は次のようになります。

上のように、 $r$ の値が変わると、共有点の数は、1個、2個、3個となるケースがあります。

なお、 $r$ を極端に大きな数や小さな数にすれば、どんな三次関数のグラフを考えても、直線との共有点の数は1個になることから、セには1が入るしかありません。

解答

セソタ：113

解答編 つづき

(3) $p\gt \dfrac{\mybox{ソ} }{\mybox{タ} }$ とし、曲線 $C$ と直線 $\ell$ が3個の共有点をもつような $r$ の値の範囲を $p$ を用いて表そう。点 $(s,f(s))$ における $C$ の接線の傾きが $-1$ となるのは $s=\pm\sqrt{\dfrac{\myBox{チ}p-\myBox{ツ} }{\myBox{テ}p} }$ のときである。したがって、傾きが $-1$ となる $C$ の接線は2本あり、 $\ell$ がこれらの接線のどちらかに一致するとき、 $C$ と $\ell$ の共有点は、 $\myBox{ト}$ 個となる。①を用いて、これら2本の接線と y 軸との交点を求めれば、 $C$ と $\ell$ が3個の共有点をもつような $r$ の絶対値の範囲は\[ |r|\lt \frac{\myBox{ナ}p-\myBox{ニ} }{\myBox{ヌ} } \sqrt{\dfrac{\mybox{チ}p-\mybox{ツ} }{\mybox{テ}p} } \]であることがわかる。

解説

点 $(s,f(s))$ における $C$ の接線の傾きは、(1)で見た通り $f'(s)=3ps^2-3p$ です。なので、これが $-1$ となるのは
\begin{eqnarray} 3ps^2-3p &=& -1 \\[5pt] s^2 &=& \frac{3p-1}{3p} \\[5pt] \end{eqnarray}が成り立つときです。今考えているのは $p\gt \dfrac{1}{3}$ のときなので、右辺は正だから\[ s=\pm\sqrt{\dfrac{3p-1}{3p} } \]だと求められます。

傾きが $-1$ の接線と $\ell$ とが一致するのは、次のような場合です。

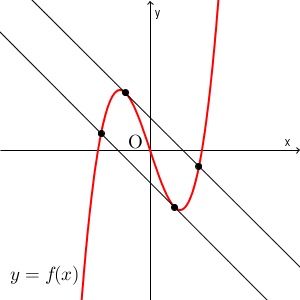
よって、このとき、 $C$ と $\ell$ との共有点は2個となります。

①より、接線と $y$ 軸との交点の $y$ 座標は $-2ps^3$ です。これに先ほどの値を入れてみます。 $s=\sqrt{\dfrac{3p-1}{3p} }$ とすると
\begin{eqnarray} & & -2p\cdot \dfrac{3p-1}{3p}\cdot \sqrt{\dfrac{3p-1}{3p} } \\[5pt] & & -\dfrac{2(3p-1)}{3}\sqrt{\dfrac{3p-1}{3p} } \\[5pt] \end{eqnarray}となります。 $s=-\sqrt{\dfrac{3p-1}{3p} }$ のときは、符号が変わるだけです。

これより、 $r$ を動かしたとき、 $C$ と $\ell$ との共有点が3個となるような $r$ の範囲は、先ほど求めた2つの $y$ 座標の間であることから\[ |r|\lt \dfrac{6p-2}{3}\sqrt{\dfrac{3p-1}{3p} } \]のときであることがわかります。

解答

チツテ：313
ト：2
ナニヌ：623

解答編 つづき

(4) $u$ を $1$ 以上の実数とする。 $t$ が $t\gt u$ の範囲を動くとき、曲線 $y=x^2-1$ と $x$ 軸および2直線 $x=u$, $x=t$ で囲まれた図形の面積が $f(t)$ とつねに等しいとする。このとき、 $p=\dfrac{\myBox{ネ} }{\myBox{ノ} }$ であり、 $u=\sqrt{\myBox{ハ} }$ となる。

解説

$u\gt 1$ なので、 $u\leqq x\leqq t$ の間では、 $x^2-1$ は正です。なので、 $y=x^2-1$ と $x$ 軸、 $x=u$, $x=t$ で囲まれた図形の面積は
\begin{eqnarray} & & \int_u^t (x^2-1)dx \\[5pt] &=& \left[ \dfrac{1}{3}x^3-x \right]_u^t \\[5pt] &=& \dfrac{1}{3}t^3-t -\dfrac{1}{3}u^3+u \\[5pt] \end{eqnarray}となります。これが $f(t)=pt^3-3pt$ とつねに等しいということは、 $t$ についての恒等式であるということです。これらは $t$ の多項式で表されているので、係数比較をすればいいですね。 $t^3$, $t$ の係数を比較して、\[ p=\dfrac{1}{3} \]と求められます。また、定数項を比較して \begin{eqnarray} -\frac{1}{3}u^3+u &=& 0 \\[5pt] u(u^2-3) &=& 0 \\[5pt] u &=& 0,\pm\sqrt{3} \\[5pt] \end{eqnarray}となります。 $u\gt 1$ なので、 $u=\sqrt{3}$ となります。

なお、微分積分学の基本定理を使うこともできます。一般に、\[ \dfrac{d}{dt}\int_a^t h(x)dx=h(t) \]が成り立ちます。これより、面積を $t$ で微分すれば、 $t^2-1$ となり、これが $f'(t)=3pt^2-3p$ となることから $p=\dfrac{1}{3}$ と求めることもできます。 $t=u$ のときは面積は $0$ となるので、 $f(u)=0$ であることから、上と同じ式を解いて $u=\sqrt{3}$ と求められます。

解答

ネノハ：133