センター試験 数学I・数学A 2018年度 第2問 [2] 解説
【必答問題】
問題編
問題
ある陸上競技大会に出場した選手の身長(単位はcm)と体重(単位はkg)のデータが得られた。男子短距離、男子長距離、女子短距離、女子長距離の四つのグループに分けると、それぞれのグループの選手数は、男子短距離が328人、男子長距離が271人、女子短距離が319人、女子長距離が263人である。
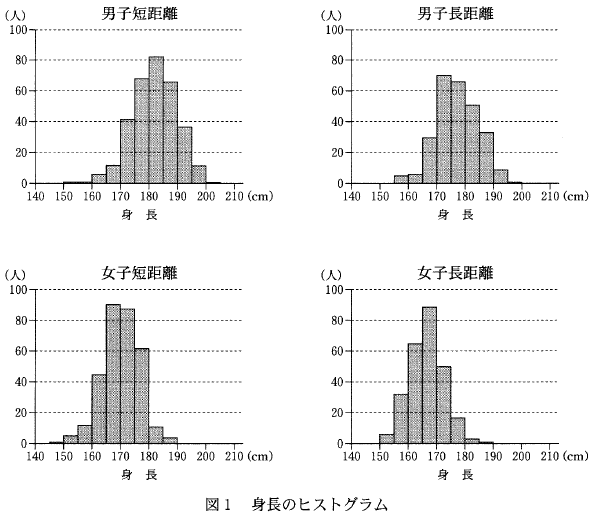
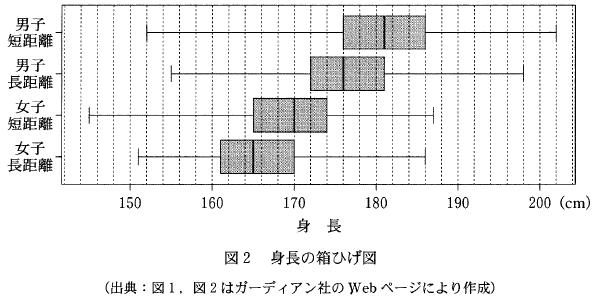
(1) 次ページの図1および図2は、男子短距離、男子長距離、女子短距離、女子長距離の四つのグループにおける、身長のヒストグラムおよび箱ひげ図である。
次の $\mybox{サ}$, $\mybox{シ}$ に当てはまるものを、下の 0 ~ 6 のうちから一つずつ選べ。ただし、解答の順序は問わない。
図1および図2から読み取れる内容として正しいものは、 $\myBox{サ}$, $\myBox{シ}$ である。
0: 四つのグループのうちで範囲が最も大きいのは、女子短距離グループである。
1: 四つのグループのすべてにおいて、四分位範囲は12未満である。
2: 男子長距離グループのヒストグラムでは、度数最大の階級に中央値が入っている。
3: 女子長距離グループのヒストグラムでは、度数最大の階級に第1四分位数が入っている。
4: すべての選手の中で最も身長の高い選手は、男子長距離グループの中にいる。
5: すべての選手の中で最も身長の低い選手は、女子長距離グループの中にいる。
6: 男子短距離グループの中央値と男子長距離グループの第3四分位数は、ともに180以上182未満である。
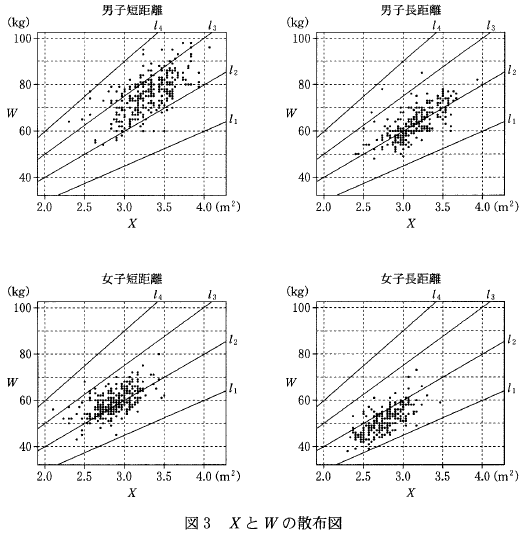
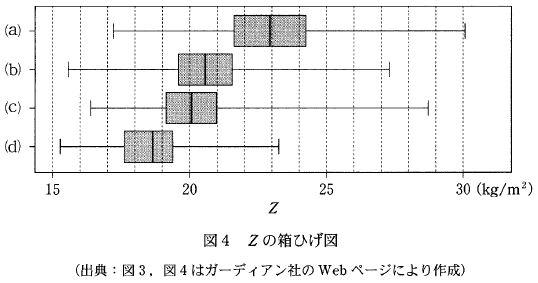
(2) 身長を H, 体重を W とし、 X を $X=\left(\dfrac{H}{100}\right)^2$ で、 Z を $Z=\dfrac{W}{X}$ で定義する。次ページの図3は、男子短距離、男子長距離、女子短距離、女子長距離の四つのグループにおける X と W のデータの散布図である。ただし、原点を通り、傾きが 15, 20, 25, 30 である四つの直線 $l_1$, $l_2$, $l_3$, $l_4$ も補助的に描いている。また、次ページの図4の (a), (b), (c), (d) で示す Z の四つの箱ひげ図は、男子短距離、男子長距離、女子短距離、女子長距離の四つのグループのいずれかの箱ひげ図に対応してる。
次の $\mybox{ス}$, $\mybox{セ}$ に当てはまるものを、下の 0 ~ 5 のうちから一つずつ選べ。ただし、解答の順序は問わない。
図3および図4から読み取れる内容として正しいものは、 $\myBox{ス}$, $\myBox{セ}$ である。
0: 四つのグループのすべてにおいて、 X と W には負の相関がある。
1: 四つのグループのうちで Z の中央値が市場の沖いのは、男子長距離グループである。
2: 四つのグループのうちで Z の範囲が最小なのは、男子長距離グループである。
3: 四つのグループのうちで Z の四分位範囲が最小なのは、男子短距離グループである。
4: 女子長距離グループのすべての Z の値は25より小さい。
5: 男子長距離グループの Z の箱ひげ図は(c)である。
(3) n を自然数とする。実数値のデータ $x_1, x_2,\cdots,x_n$ および $w_1, w_2, \cdots, w_n$ に対して、それぞれの平均値を\[ \bar{x}=\frac{x_1+x_2+\cdots+x_n}{n}, \ \bar{w}=\frac{w_1+w_2+\cdots+w_n}{n} \]とおく。等式 $(x_1+x_2+\cdots+x_n)\bar{w}=n\bar{x}\bar{w}$ などに注意すると、偏差の積の和は
\begin{eqnarray} & & (x_1-\bar{x})(w_1-\bar{w})+(x_2-\bar{x})(w_2-\bar{w})+\cdots+(x_n-\bar{x})(w_n-\bar{w}) \\[5pt] & & =x_1w_1+x_2w_2+\cdots+x_nw_n-\myBox{ソ} \end{eqnarray} となることがわかる。 $\mybox{ソ}$ に当てはまるものを、次の 0 ~ 3 のうちから一つ選べ。0: $\bar{x}\bar{w}$
1: $(\bar{x}\bar{w})^2$
2: $n \bar{x}\bar{w}$
3: $n^2 \bar{x}\bar{w}$
考え方
(1)は、それぞれの用語が何を表しているかが分かれば難しくはないでしょう。
(2)は、散布図にひかれた線と Z の箱ひげ図とがどう対応しているかを考える必要があります。直線の傾きと箱ひげ図の目盛りを見れば、想像はつくと思いますが。はじめに、箱ひげ図がどのグループを指しているかを特定したほうが早く考えられるかもしれません。
(3)は、計算問題です。足す順番を変えて計算します。ヒントも出ているので、足す順番の入れ替え方を思いつくかもしれませんが、抽象的な計算に慣れていないと少し難しいかもしれません。
【必答問題】
解答編
問題
ある陸上競技大会に出場した選手の身長(単位はcm)と体重(単位はkg)のデータが得られた。男子短距離、男子長距離、女子短距離、女子長距離の四つのグループに分けると、それぞれのグループの選手数は、男子短距離が328人、男子長距離が271人、女子短距離が319人、女子長距離が263人である。
(1) 次ページの図1および図2は、男子短距離、男子長距離、女子短距離、女子長距離の四つのグループにおける、身長のヒストグラムおよび箱ひげ図である。
次の $\mybox{サ}$, $\mybox{シ}$ に当てはまるものを、下の 0 ~ 6 のうちから一つずつ選べ。ただし、解答の順序は問わない。
図1および図2から読み取れる内容として正しいものは、 $\myBox{サ}$, $\myBox{シ}$ である。
0: 四つのグループのうちで範囲が最も大きいのは、女子短距離グループである。
1: 四つのグループのすべてにおいて、四分位範囲は12未満である。
2: 男子長距離グループのヒストグラムでは、度数最大の階級に中央値が入っている。
3: 女子長距離グループのヒストグラムでは、度数最大の階級に第1四分位数が入っている。
4: すべての選手の中で最も身長の高い選手は、男子長距離グループの中にいる。
5: すべての選手の中で最も身長の低い選手は、女子長距離グループの中にいる。
6: 男子短距離グループの中央値と男子長距離グループの第3四分位数は、ともに180以上182未満である。
解説
一つ一つ見ていきましょう。
0について、「範囲」とは、最大値と最小値との差のことなので、箱ひげ図を見ましょう。男子短距離と長距離を比べると、短距離の方が横に長いので、範囲が大きいことがわかります。50くらいありますね。女子を見ると、両方とも50より小さいです。なので、範囲が最も大きいのは男子短距離なので、0は正しくありません。
1について、「四分位範囲」とは、第三四分位数と第一四分位数との差なので、これも箱ひげ図を見ます。箱の横幅を見ればいいですね。箱の横幅は、どれも6目盛り未満です。一つの目盛りが2なので、四分位範囲は、どれも12未満です。1は正しいです。
2について、「中央値」は、箱ひげ図の箱の中にある線を見ればわかります。男子長距離の中央値は、箱ひげ図をみると176くらいだとわかります。一方、ヒストグラムを見ると、度数が最大の階級は170~175なので、ここに中央値は入っていません。2は正しくありません。
3について、「第1四分位数」は、箱ひげ図の箱の左端を見ればわかります。女子長距離の第1四分位数は、161くらいですね。一方、ヒストグラムを見ると、度数が最大の階級は、165~170なので、ここに第1四分位数は入っていません。3は正しくありません。
4について、最も身長が高いのは、箱ひげ図の右端を見れば、男子短距離のグループの中にいることがわかります。4は正しくありません。
5について、最も身長が低いのは、箱ひげ図の左端を見ると、女子短距離のグループの中にいることがわかります。5は正しくありません。
6について、箱ひげ図を見ると、男子短距離グループの中央値も、男子長距離グループの第3四分位数も、181程度であることがわかります。よって、ともに180以上182未満です。6は正しいです。
以上から、1と6が正しいことがわかります。
解答
サシ:1・6
参考
解答編 つづき
問題
(2) 身長を H, 体重を W とし、 X を $X=\left(\dfrac{H}{100}\right)^2$ で、 Z を $Z=\dfrac{W}{X}$ で定義する。次ページの図3は、男子短距離、男子長距離、女子短距離、女子長距離の四つのグループにおける X と W のデータの散布図である。ただし、原点を通り、傾きが 15, 20, 25, 30 である四つの直線 $l_1$, $l_2$, $l_3$, $l_4$ も補助的に描いている。また、次ページの図4の (a), (b), (c), (d) で示す Z の四つの箱ひげ図は、男子短距離、男子長距離、女子短距離、女子長距離の四つのグループのいずれかの箱ひげ図に対応してる。
次の $\mybox{ス}$, $\mybox{セ}$ に当てはまるものを、下の 0 ~ 5 のうちから一つずつ選べ。ただし、解答の順序は問わない。
図3および図4から読み取れる内容として正しいものは、 $\myBox{ス}$, $\myBox{セ}$ である。
0: 四つのグループのすべてにおいて、 X と W には負の相関がある。
1: 四つのグループのうちで Z の中央値が市場の沖いのは、男子長距離グループである。
2: 四つのグループのうちで Z の範囲が最小なのは、男子長距離グループである。
3: 四つのグループのうちで Z の四分位範囲が最小なのは、男子短距離グループである。
4: 女子長距離グループのすべての Z の値は25より小さい。
5: 男子長距離グループの Z の箱ひげ図は(c)である。
解説
Z は、いわゆる、BMIですね。選択肢を一つ一つ見ていきましょう。
0について、「負の相関がある」というのは、片方が増えるともう片方が減る傾向にあることを言います。しかし、散布図を見ると、片方が増えるともう片方も増える、正の相関があることが見て取れます。よって、0は正しくありません。
1以降を考える前に、箱ひげ図がそれぞれどれに対応しているかを見ておきましょう。
箱ひげ図にひかれている線の見方を考えましょう。 $\dfrac{W}{X}$ というのは、その点と原点とを結んだ直線の傾きを表しています。なので、例えば、散布図上で、ある点が $l_2$ と $l_3$ の間にある、ということは、傾きが20と25の間にあるということ、 Z が20と25の間にあるということを表しています。これが箱ひげ図の20と25の間の部分に対応しているということです。これを踏まえて考えます。
一番特徴的なのは(d)です。これは箱全体が20以下となっています。 Z の大半が20以下ということは、散布図で見たときに、傾き20の直線より下にあることを表しています。 $l_2$ より下に点が集中しているものを見ると、(d)は女子長距離であることがわかります。
次に(a)を見てみましょう。最大値が少し30を超えています。よって、 $l_4$ を少し超えているようなグループを探せばいいですね。このことから、男子短距離であることがわかります。
最後の(b)と(c)は少し難しいです。 Z の値の中央部分を見ても、散布図では点が密集している部分に対応しているので考えづらいです。(a)のときのように、最大と最小の部分、端っこの部分で考えましょう。
最小値で見ると、(b)の方が小さく、15に近いです。これを踏まえると、 $l_1$ に近い点がある、女子短距離が(b)であると考えられます。また、最大値を考えると、(c)の方が大きく、30に近いです。これを踏まえると、 $l_4$ に近い点がある男子長距離が(c)であると考えられます。
以上より、(a)男子短距離、(b)女子短距離、(c)男子長距離、(d)女子長距離だとわかります。
さて、選択肢を見ていきましょう。
1について、 Z の中央値が一番大きいのは(a)ですが、これは男子短距離です。これは正しくありません。
2について、 Z の範囲が最小なのは(d)ですが、これは女子長距離です。これは正しくありません。
3について、四分位範囲が最小なのは、パッとはどれかはわかりにくいですが、少なくとも(a)ではありません。男子短距離ではないので、これも正しくありません。
4について、女子長距離は(d)で、確かにどの値も25より小さいです。正しいです。
5について、男子長距離は(c)です。正しいです。
以上から、4と5が正しいことがわかります。
解答
スセ:4・5
参考
解答編 つづき
問題
(3) n を自然数とする。実数値のデータ $x_1, x_2,\cdots,x_n$ および $w_1, w_2, \cdots, w_n$ に対して、それぞれの平均値を\[ \bar{x}=\frac{x_1+x_2+\cdots+x_n}{n}, \ \bar{w}=\frac{w_1+w_2+\cdots+w_n}{n} \]とおく。等式 $(x_1+x_2+\cdots+x_n)\bar{w}=n\bar{x}\bar{w}$ などに注意すると、偏差の積の和は
\begin{eqnarray} & & (x_1-\bar{x})(w_1-\bar{w})+(x_2-\bar{x})(w_2-\bar{w})+\cdots+(x_n-\bar{x})(w_n-\bar{w}) \\[5pt] & & =x_1w_1+x_2w_2+\cdots+x_nw_n-\myBox{ソ} \end{eqnarray} となることがわかる。 $\mybox{ソ}$ に当てはまるものを、次の 0 ~ 3 のうちから一つ選べ。0: $\bar{x}\bar{w}$
1: $(\bar{x}\bar{w})^2$
2: $n \bar{x}\bar{w}$
3: $n^2 \bar{x}\bar{w}$
解説
$(x_1-\bar{x})(w_1-\bar{w})$ を展開すると、
\[ x_1w_1 -\bar{w}x_1 -\bar{x}w_1 +\bar{x}\bar{w} \]が出てきます。同じように計算すれば、 $i$ 番目の積は
\[ x_iw_i -\bar{w}x_i -\bar{x}w_i +\bar{x}\bar{w} \]が出てきます。これを $i$ について、 $1$ から $n$ まで足し合わせればいいですね。4つの項について、それぞれ考えていきましょう。
まず、1つ目の $x_iw_i$ は、 $x_1w_1+x_2w_2+\cdots+x_nw_n$ となります。これが、変形後のソの前の部分です。
次に、2つ目の $-\bar{w}x_i$ について考えましょう。ここでは、 $\bar{w}$ は $i$ に関係のない定数なので、 $i$ について足し合わせれば、 $x_1$ から $x_n$ までの和に $-\bar{w}$ を掛けたものになります。問題文中のヒントにある通り、平均値の定義から、 $x_1$ から $x_n$ までの和は $n\bar{x}$ なのだから、この部分の和は $-n\bar{x}\bar{w}$ となることがわかります。
続いて、3つ目の $-\bar{x}w_i$ についてです。同様に考えていきます。 $\bar{x}$ は $i$ に関係のない定数なので、 $i$ について足し合わせれば、 $w_1$ から $w_n$ までの和に $-\bar{x}$ を掛けたものになります。 $w_1$ から $w_n$ までの和は $n\bar{w}$ なのだから、この部分の和は $-n\bar{x}\bar{w}$ となることがわかります。
残りは、 $\bar{x}\bar{w}$ の部分です。 $i$ に関して定数なので、和は単に $n$ 倍したものとなります。つまり、 $n \bar{x}\bar{w}$ です。
以上から、
\begin{eqnarray}
& &
(x_1-\bar{x})(w_1-\bar{w})+(x_2-\bar{x})(w_2-\bar{w})+\cdots+(x_n-\bar{x})(w_n-\bar{w}) \\[5pt]
&=& x_1w_1+x_2w_2+\cdots+x_nw_n -n \bar{x}\bar{w} -n \bar{x}\bar{w} +n \bar{x}\bar{w} \\[5pt]
&=& x_1w_1+x_2w_2+\cdots+x_nw_n -n \bar{x}\bar{w}
\end{eqnarray}
となります。
解答
ソ:2