センター試験 数学I・数学A 2018年度 第2問 [1] 解説
【必答問題】
問題編
問題
四角形 ABCD において、3辺の長さをそれぞれ $\mathrm{ AB }=5$, $\mathrm{ BC }=9$, $\mathrm{ CD }=3$, 対角線 AC の長さを $\mathrm{ AC }=6$ とする。このとき\[ \cos \angle \mathrm{ ABC }=\frac{\myBox{ア} }{\myBox{イ} }, \ \sin \angle \mathrm{ ABC } = \frac{\myBox{ウ}\sqrt{\myBox{エ} }}{\myBox{オ} } \]である。
ここで、四角形 ABCD は台形であるとする。
次の $\mybox{カ}$ には下の 0 ~ 2 から、 $\mybox{キ}$ には 3, 4 から当てはまるものを一つずつ選べ。
CD $\myBox{カ}$ AB $\cdot \sin \angle \mathrm{ ABC }$ であるから $\myBox{キ}$ である。
0: $\lt$
1: $=$
2: $\gt$3: 辺 AD と辺 BC が平行
4: 辺 AB と辺 CD が平行したがって\[ \mathrm{ BD }=\myBox{ク} \sqrt{\myBox{ケコ} } \]である。
考え方
前半はいいとして、後半はわかりづらいです。キは、カの不等式を使うと、どちらかの場合で矛盾が生じます。そのことから答えを絞ることになります。なかなか気づきにくいでしょう。
最後も、なかなか難しいです。正確に図をかけば、今までの計算を応用して求めることがわかりますが、難しいです。難しく考えて方針を間違うと、深みにはまってしまいます。
【必答問題】
解答編
問題
四角形 ABCD において、3辺の長さをそれぞれ $\mathrm{ AB }=5$, $\mathrm{ BC }=9$, $\mathrm{ CD }=3$, 対角線 AC の長さを $\mathrm{ AC }=6$ とする。このとき\[ \cos \angle \mathrm{ ABC }=\frac{\myBox{ア} }{\myBox{イ} }, \ \sin \angle \mathrm{ ABC } = \frac{\myBox{ウ}\sqrt{\myBox{エ} }}{\myBox{オ} } \]である。
解説
三角形 ABC の3辺の長さが分かっているので、余弦定理を使いましょう。
\begin{eqnarray}
\cos\angle \mathrm{ ABC }
&=&
\frac{\mathrm{ AB }^2+\mathrm{ BC }^2-\mathrm{ AC }^2}{2 \mathrm{ AB }\cdot \mathrm{ BC } } \\[5pt]
&=&
\frac{5^2+9^2-6^2}{2 \cdot 5 \cdot 9} \\[5pt]
&=&
\frac{25+81-36}{2 \cdot 5 \cdot 9} \\[5pt]
&=&
\frac{70}{2 \cdot 5 \cdot 9} \\[5pt]
&=&
\frac{7}{9} \\[5pt]
\end{eqnarray}となります。
三角比の相互関係より
\begin{eqnarray}
\sin^2 \angle \mathrm{ ABC }+\cos^2 \angle \mathrm{ ABC } &=& 1 \\[5pt]
\sin^2 \angle \mathrm{ ABC }+\frac{49}{81} &=& 1 \\[5pt]
\sin^2 \angle \mathrm{ ABC } &=& \frac{32}{81} \\[5pt]
\end{eqnarray}となります。今考えている範囲では、 $\sin\angle \mathrm{ ABC }$ の値は正なので、\[ \sin \angle \mathrm{ ABC } = \frac{4\sqrt{2} }{9} \]となります。
解答
アイ:79
ウエオ:429
解答編 つづき
問題
ここで、四角形 ABCD は台形であるとする。
次の $\mybox{カ}$ には下の 0 ~ 2 から、 $\mybox{キ}$ には 3, 4 から当てはまるものを一つずつ選べ。
CD $\myBox{カ}$ AB $\cdot \sin \angle \mathrm{ ABC }$ であるから $\myBox{キ}$ である。
0: $\lt$
1: $=$
2: $\gt$3: 辺 AD と辺 BC が平行
4: 辺 AB と辺 CD が平行
解説
$\mathrm{ CD }=3$ です。また、先ほどの計算から
\begin{eqnarray}
\mathrm{ AB } \cdot \sin \angle \mathrm{ ABC }
&=&
5\cdot \frac{4\sqrt{2} }{9} \\[5pt]
&=&
\frac{20\sqrt{2} }{9} \\[5pt]
\end{eqnarray}となります。これを2乗すると、 $\dfrac{800}{81}$ なので、 $3^2$ より大きいです。このことから、\[ \mathrm{ CD } \lt \mathrm{ AB } \cdot \sin \angle \mathrm{ ABC } \]となることがわかります。
四角形 ABCD は台形なので、辺 AD と辺 BC が平行か、辺 AB と辺 CD が平行となります。上で見た不等式がどう関係するか、考えてみましょう。
もし、 AD と辺 BC が平行であれば、図は次のようになります。(長さなどは適当です)
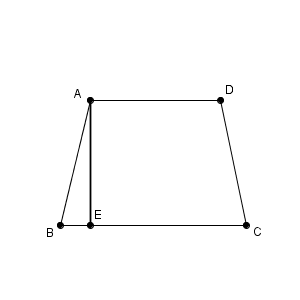
ここで、 $\mathrm{ AB } \cdot \sin \angle \mathrm{ ABC }$ が何を表しているかを考えると、 A から BC にひいた垂線の長さ(台形の高さ)になることがわかります。これは、 AD と BC との距離なので、 CD がこれより短くなることはありません。なので、先ほど得られた不等式と矛盾することがわかります。
以上から、平行な辺は、辺 AB と辺 CD であることがわかります。
解答
カ:0
キ:4
解答編 つづき
問題
したがって\[ \mathrm{ BD }=\myBox{ク} \sqrt{\myBox{ケコ} } \]である。
解説
先ほどの結果から、四角形 ABCD は次のようになります。
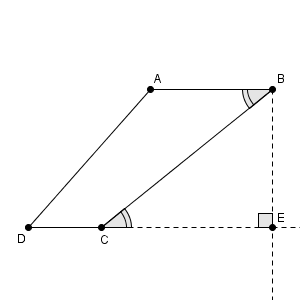
B から直線 CD に下した垂線の足を E としています。冒頭で見た通り、 $\cos\angle \mathrm{ ABC }$ は正なので、角度は鋭角であることがわかります。 AB と CD が平行だから、 $\angle \mathrm{ BCE }=\angle \mathrm{ ABC }$ であることがわかります。
よって、冒頭の計算から、
\begin{eqnarray}
\mathrm{ CE }
&=&
\mathrm{ BC } \times \cos \angle \mathrm{ ABC } \\[5pt]
&=&
9 \times \frac{7}{9} \\[5pt]
&=&
7
\end{eqnarray}なので、 $\mathrm{ DE }=7+3=10$ であることがわかります。また、
\begin{eqnarray}
\mathrm{ BE }
&=&
\mathrm{ BC } \times \sin \angle \mathrm{ ABC } \\[5pt]
&=&
9 \times \frac{4\sqrt{2} }{9} \\[5pt]
&=&
4\sqrt{2}
\end{eqnarray}となります。
よって、三角形 BDE に対して三平方の定理を使うと
\begin{eqnarray}
\mathrm{ BD }^2
&=&
10^2 +(4\sqrt{2})^2 \\[5pt]
&=&
132
\end{eqnarray}なので、 $\mathrm{ BD }=2\sqrt{33}$ と求められます。
解答
クケコ:233





