センター試験数学I・数学A 2017年度第5問解説

🕒 2017/01/16 🔄 2023/05/01

【選択問題】(第3問～第5問から2問選択)

問題編

問題

　$\triangle \mathrm{ ABC }$ において、 $\mathrm{ AB }=3$, $\mathrm{ BC }=8$, $\mathrm{ AC }=7$ とする。

(1) 辺 AC 上に点 D を $\mathrm{ AD }=3$ となるようにとり、 $\triangle \mathrm{ ABD }$ の外接円と直線 BC の交点で B と異なるものを E とする。このとき、 $\mathrm{ BC }\cdot \mathrm{ CE }=\myBox{アイ}$ であるから、 $\displaystyle \mathrm{ CE }=\frac{\myBox{ウ} }{\myBox{エ} }$ である。

　直線 AB と直線 DE の交点を F とするとき、 $\displaystyle \frac{\mathrm{ BF } }{\mathrm{ AF } } = \frac{\myBox{オカ} }{\myBox{キ} }$ であるから、 $\displaystyle \mathrm{ AF }=\frac{\myBox{クケ} }{\myBox{コ} }$ である。

(2) $\angle \mathrm{ ABC }=\myBox{サシ}^{\circ}$ である。 $\triangle \mathrm{ ABC }$ の内接円の半径は $\displaystyle \frac{\myBox{ス}\sqrt{\myBox{セ} }}{\myBox{ソ} }$ であり、 $\triangle \mathrm{ ABC }$ の内心を I とすると $\displaystyle \mathrm{ BI }=\frac{\myBox{タ}\sqrt{\myBox{チ} }}{\myBox{ツ} }$ である。

考え方

図形をきちんとかいて、方べきの定理やメネラウスの定理を使うようにしましょう。

(2)は余弦定理を使うこともできますし、使わなくても解くことができます。内接円の半径を求めるときは、三角形の面積を考えると解きやすくなります。一番最後は、角度をうまく使うとほとんど計算せずに解けます。

【選択問題】(第3問～第5問から2問選択)

解答編

問題

　$\triangle \mathrm{ ABC }$ において、 $\mathrm{ AB }=3$, $\mathrm{ BC }=8$, $\mathrm{ AC }=7$ とする。

(1) 辺 AC 上に点 D を $\mathrm{ AD }=3$ となるようにとり、 $\triangle \mathrm{ ABD }$ の外接円と直線 BC の交点で B と異なるものを E とする。このとき、 $\mathrm{ BC }\cdot \mathrm{ CE }=\myBox{アイ}$ であるから、 $\displaystyle \mathrm{ CE }=\frac{\myBox{ウ} }{\myBox{エ} }$ である。

解説

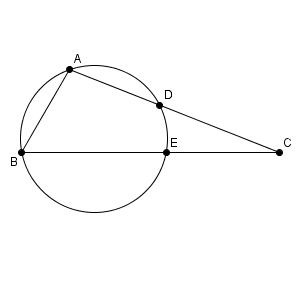
方べきの定理より
\begin{eqnarray} \mathrm{ BC }\cdot \mathrm{ CE } &=& \mathrm{ AC }\cdot \mathrm{ CD } \\ &=& 7\cdot (7-3) \\ &=& 28 \\ \end{eqnarray}となります。よって \begin{eqnarray} \mathrm{ CE } &=& \frac{28}{\mathrm{ BC } } \\[5pt] &=& \frac{28}{8} \\[5pt] &=& \frac{7}{2} \\[5pt] \end{eqnarray}となります。

解答

アイ：28
ウエ：72

解答編つづき

問題

　直線 AB と直線 DE の交点を F とするとき、 $\displaystyle \frac{\mathrm{ BF } }{\mathrm{ AF } } = \frac{\myBox{オカ} }{\myBox{キ} }$ であるから、 $\displaystyle \mathrm{ AF }=\frac{\myBox{クケ} }{\myBox{コ} }$ である。

解説

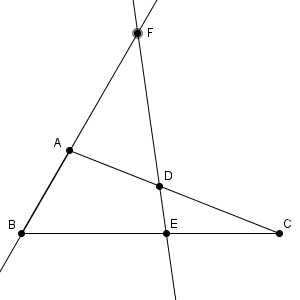
メネラウスの定理より
\begin{eqnarray} \frac{\mathrm{ BF } }{\mathrm{ AF } } \cdot \frac{\mathrm{ AD } }{\mathrm{ DC } } \cdot \frac{\mathrm{ CE } }{\mathrm{ BE } } &=& 1 \\[5pt] \frac{\mathrm{ BF } }{\mathrm{ AF } } \cdot \frac{3}{4} \cdot \frac{\frac{7}{2} }{8-\frac{7}{2} } &=& 1 \\[5pt] \frac{\mathrm{ BF } }{\mathrm{ AF } } \cdot \frac{3\times7}{4\times9} &=& 1 \\[5pt] \frac{\mathrm{ BF } }{\mathrm{ AF } } &=& \frac{12}{7} \\[5pt] \end{eqnarray}となります。

$\mathrm{ AF }=x$ とすると、 $\mathrm{ BF }=x+3$ なので、これを上に代入すると
\begin{eqnarray} \frac{x+3}{x} &=& \frac{12}{7} \\[5pt] 7(x+3) &=& 12x \\[5pt] 12x-7x &=& 21 \\[5pt] x &=& \frac{21}{5} \\[5pt] \end{eqnarray}となります。

解答

オカキ：127
クケコ：215

解答編つづき

問題

(2) $\angle \mathrm{ ABC }=\myBox{サシ}^{\circ}$ である。

解説

余弦定理を使うこともできますが、ここでは別の解き方で解いてみます。

A から BC に垂線をおろし、その足を G とします。

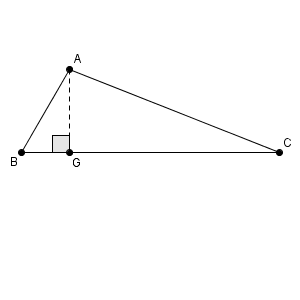
$\mathrm{ BG }=x$ とおいて、三平方の定理を用いて $\mathrm{ AG }^2$ を2通りで表現すると
\begin{eqnarray} \mathrm{ AB }^2 -\mathrm{ BG }^2 &=& \mathrm{ AC }^2 -\mathrm{CG}^2 \\ 3^2 -x^2 &=& 7^2 -(8-x)^2 \\ x^2-16x+64 -x^2 &=& 49-9 \\ -16x &=& 40-64 \\ x &=& \frac{3}{2} \\ \end{eqnarray}よって、 $\displaystyle \mathrm{ BG } =\frac{3}{2}$ で　$\mathrm{ AB }=3$ だから、 $\angle \mathrm{ ABC }=60^{\circ}$ となることがわかります。

なお、余弦定理を用いれば
\begin{eqnarray} \cos\angle \mathrm{ ABC } &=& \frac{\mathrm{ AB }^2+\mathrm{ BC }^2-\mathrm{ AC }^2}{ 2\mathrm{ AB }\cdot\mathrm{ BC } } \\[5pt] &=& \frac{3^2+8^2-7^2}{ 2\cdot3\cdot8 } \\[5pt] &=& \frac{24}{ 48 } \\[5pt] &=& \frac{1}{2} \\[5pt] \end{eqnarray}から $\angle \mathrm{ ABC }=60^{\circ}$ と導くこともできます。

解答

サシ：60

解答編つづき

問題

$\triangle \mathrm{ ABC }$ の内接円の半径は $\displaystyle \frac{\myBox{ス}\sqrt{\myBox{セ} }}{\myBox{ソ} }$ であり、 $\triangle \mathrm{ ABC }$ の内心を I とすると $\displaystyle \mathrm{ BI }=\frac{\myBox{タ}\sqrt{\myBox{チ} }}{\myBox{ツ} }$ である。

解説

I から BC に下した垂線の足を H とします。

$\angle \mathrm{ ABC }=60^{\circ}$ なので、 BC を底辺とすると高さは $\frac{3\sqrt{3} }{2}$ となるから、三角形 ABC の面積は
\begin{eqnarray} \frac{1}{2} \times 8 \times \frac{3\sqrt{3} }{2} = 6\sqrt{3} \end{eqnarray}となります。