センター試験 数学I・数学A 2018年度 第5問 解説
【選択問題】(第3問~第5問から2問選択)
問題編
問題
$\triangle \mathrm{ ABC }$ において $\mathrm{ AB }=2$, $\mathrm{ AC }=1$, $\angle \mathrm{ A }=90^{\circ}$ とする。
$\angle \mathrm{ A }$ の二等分線と辺 BC との交点を D とすると、 $\mathrm{ BD }=\dfrac{\myBox{ア}\sqrt{\myBox{イ} }}{\myBox{ウ} }$ である。
点 A を通り点 D で辺 BC に接する円と辺 AB との交点で A と異なるものを E とすると、 $\mathrm{ AB }\cdot \mathrm{ BE }=\dfrac{\myBox{エオ} }{\myBox{カ} }$ であるから、 $\mathrm{ BE }=\dfrac{\myBox{キク} }{\myBox{ケ} }$ である。
次の $\mybox{コ}$ には下の 0 ~ 2 から、 $\mybox{サ}$ には 3・4 から当てはまるものを一つずつ選べ。
$\dfrac{\mathrm{ BE } }{\mathrm{ BD } } \myBox{コ} \dfrac{\mathrm{ AB } }{\mathrm{ BC } }$ であるから、直線 AC と直線 DE の交点は辺 AC の端点 $\myBox{サ}$ の側の延長線上にある。
0: $\lt$
1: $=$
2: $\gt$3: A
4: Cその交点を F とすると、 $\dfrac{\mathrm{ CF } }{\mathrm{ AF } }=\dfrac{\myBox{シ} }{\myBox{ス} }$ であるから、 $\mathrm{ CF }=\dfrac{\myBox{セ} }{\myBox{ソ} }$ である。したがって、 BF の長さが求まり、 $\dfrac{\mathrm{ CF } }{\mathrm{ AC } }=\dfrac{\mathrm{ BF } }{\mathrm{ AB } }$ であることがわかる。
次の $\mybox{タ}$ には下の 0 ~ 3 から当てはまるものを一つ選べ。
点 D は $\triangle \mathrm{ ABF }$ の $\myBox{タ}$ 。
0: 外心である
1: 内心である2: 重心である
3: 外心、内心、重心のいずれでもない
考え方
コからサの部分が少しわかりにくいですが、図をかいて考えればひらめきやすいでしょう。
タの部分も少しわかりにくいですが、直前に書かれている説明がかなり重要なヒントなので、ここも思いつくのはそれほど難しくありません。そもそも、中点や等しい長さが出てこないので重心はなさそうだし、垂線も出てこないので外心の可能性も低く、ありえるとしたら内心しかありません。と考えると、タの直線の説明をどう使うかがわかるはずです。
【選択問題】(第3問~第5問から2問選択)
解答編
問題
$\triangle \mathrm{ ABC }$ において $\mathrm{ AB }=2$, $\mathrm{ AC }=1$, $\angle \mathrm{ A }=90^{\circ}$ とする。
$\angle \mathrm{ A }$ の二等分線と辺 BC との交点を D とすると、 $\mathrm{ BD }=\dfrac{\myBox{ア}\sqrt{\myBox{イ} }}{\myBox{ウ} }$ である。
解説
図は次のようになっています。
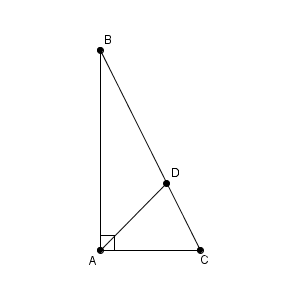
AD は $\angle \mathrm{ A }$ の二等分線なので、\[ \mathrm{ BD }:\mathrm{ CD }=\mathrm{ AB }:\mathrm{ AC }=2:1 \]となります。また、三平方の定理から $\mathrm{ BC }=\sqrt{5}$ なので、\[ \mathrm{ BD }=\frac{2\sqrt{5} }{3} \]となります。
解答
アイウ:253
解答編 つづき
問題
点 A を通り点 D で辺 BC に接する円と辺 AB との交点で A と異なるものを E とすると、 $\mathrm{ AB }\cdot \mathrm{ BE }=\dfrac{\myBox{エオ} }{\myBox{カ} }$ であるから、 $\mathrm{ BE }=\dfrac{\myBox{キク} }{\myBox{ケ} }$ である。
解説
図は次のようになっています。
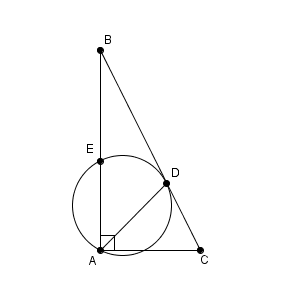
接弦定理から $\angle \mathrm{ BDE }=\angle \mathrm{ BAD }$ なので、三角形 BDE と三角形 BAD は相似です。なので、 $\mathrm{ BE }:\mathrm{ BD }=\mathrm{ BD }:\mathrm{ BA }$ だから\[ \mathrm{ AB }\cdot\mathrm{ BE }=\mathrm{ BD }^2=\frac{20}{9} \]となります。(方べきの定理と考えても構いません)
$\mathrm{ AB }=2$ なので、 $\mathrm{ BE }=\dfrac{10}{9}$ と求められます。
解答
エオカ:209
キクケ:109
解答編 つづき
問題
次の $\mybox{コ}$ には下の 0 ~ 2 から、 $\mybox{サ}$ には 3・4 から当てはまるものを一つずつ選べ。
$\dfrac{\mathrm{ BE } }{\mathrm{ BD } } \myBox{コ} \dfrac{\mathrm{ AB } }{\mathrm{ BC } }$ であるから、直線 AC と直線 DE の交点は辺 AC の端点 $\myBox{サ}$ の側の延長線上にある。
0: $\lt$
1: $=$
2: $\gt$3: A
4: C
解説
\begin{eqnarray} \frac{\mathrm{ BE } }{\mathrm{ BD } }&=&\frac{10}{9} \div \frac{2\sqrt{5} }{3} \\[5pt] &=& \frac{\sqrt{5} }{3} \end{eqnarray}であり、 \begin{eqnarray} \frac{\mathrm{ AB } }{\mathrm{ BC } }&=&\frac{2}{\sqrt{5} } \\[5pt] &=& \frac{2\sqrt{5} }{5} \end{eqnarray}となります。それぞれ2乗すると $\dfrac{5}{9}=\dfrac{25}{45}$ と $\dfrac{4}{5}=\dfrac{36}{45}$ なので、\[ \dfrac{\mathrm{ BE } }{\mathrm{ BD } } \lt \dfrac{\mathrm{ AB } }{\mathrm{ BC } } \]となります。これより、\[ \mathrm{ BE } \lt \mathrm{ BD }\times \dfrac{\mathrm{ AB } }{\mathrm{ BC } } \]なので、 D から AB に下した垂線の足を H とすると、 $\mathrm{ BE }\lt \mathrm{ BH }$ となることがわかります。
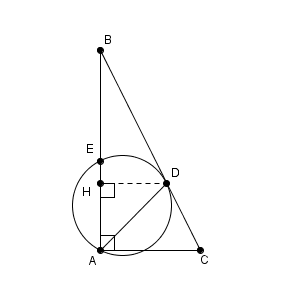
このことから、 AC と DE との交点は、辺 AC の C の側の延長線上にあることがわかります。
解答
コサ:04
解答編 つづき
問題
その交点を F とすると、 $\dfrac{\mathrm{ CF } }{\mathrm{ AF } }=\dfrac{\myBox{シ} }{\myBox{ス} }$ であるから、 $\mathrm{ CF }=\dfrac{\myBox{セ} }{\myBox{ソ} }$ である。したがって、 BF の長さが求まり、 $\dfrac{\mathrm{ CF } }{\mathrm{ AC } }=\dfrac{\mathrm{ BF } }{\mathrm{ AB } }$ であることがわかる。
次の $\mybox{タ}$ には下の 0 ~ 3 から当てはまるものを一つ選べ。
点 D は $\triangle \mathrm{ ABF }$ の $\myBox{タ}$ 。
0: 外心である
1: 内心である2: 重心である
3: 外心、内心、重心のいずれでもない
解説
図は次のようになっています。
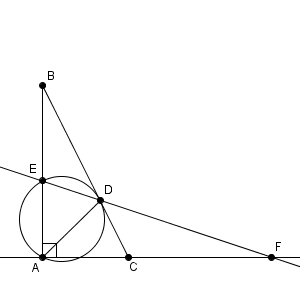
ここで、メネラウスの定理より
\begin{eqnarray}
\frac{\mathrm{ CF } }{\mathrm{ AF } } \cdot \frac{\mathrm{ DB } }{\mathrm{ CD } } \cdot \frac{\mathrm{ EA } }{\mathrm{ BE } } &=& 1 \\[5pt]
\frac{\mathrm{ CF } }{\mathrm{ AF } } \cdot \frac{\mathrm{ AB } }{\mathrm{ AC } } \cdot \frac{2-\frac{10}{9} }{\frac{10}{9} } &=& 1 \\[5pt]
\frac{\mathrm{ CF } }{\mathrm{ AF } } \cdot 2 \cdot \frac{4}{5} &=& 1 \\[5pt]
\frac{\mathrm{ CF } }{\mathrm{ AF } } &=& \frac{5}{8} \\[5pt]
\end{eqnarray}となります。
$\mathrm{ CF }=x$ とすると $\mathrm{ AF }=1+x$ なので
\begin{eqnarray}
\frac{x}{1+x} &=& \frac{5}{8} \\[5pt]
8x &=& 5(1+x) \\[5pt]
3x &=& 5 \\[5pt]
x &=& \frac{5}{3} \\[5pt]
\end{eqnarray}なので、 $\mathrm{ CF }=\dfrac{5}{3}$ となります。また、 $\mathrm{ AF }=\dfrac{8}{3}$ となることもわかります。
三平方の定理より
\begin{eqnarray}
\mathrm{ BF }^2&=&\mathrm{ AB }^2+\mathrm{ AF }^2 \\[5pt]
&=&
4+\frac{64}{9}=\frac{100}{9}
\end{eqnarray}なので、 $\mathrm{ BF }=\dfrac{10}{3}$ となります。

以上から、
\begin{eqnarray}
\frac{\mathrm{ CF } }{\mathrm{ AC } } &=& \frac{5}{3} \\[5pt]
\frac{\mathrm{ BF } }{\mathrm{ AB } } &=& \frac{10}{3}\div2=\frac{5}{3} \\[5pt]
\end{eqnarray}なので、 $\dfrac{\mathrm{ CF } }{\mathrm{ AC } }=\dfrac{\mathrm{ BF } }{\mathrm{ AB } }$ が成り立つことがわかります。
これより、 $\mathrm{ AB }:\mathrm{ BF }=\mathrm{ AC }:\mathrm{ CF }$ だから、 BC は $\angle \mathrm{ ABF }$ の二等分線であることがわかります。 AD は $\angle \mathrm{ BAF }$ の二等分線だったので、点 D は三角形 ABF の内心であることがわかります。
解答
シス:58
セソ:53
タ:1





