センター試験数学I・数学A 2015年度第6問解説

🕒 2016/03/06 🔄 2023/05/01

問題編

問題

　$\triangle \mathrm{ ABC }$ において、$\mathrm{ AB }=\mathrm{ AC }=5$、$\mathrm{ BC }=\sqrt{5}$ とする。辺AC 上に点D を $\mathrm{ AD }=3$ となるようにとり、辺BC の B の側の延長と $\triangle \mathrm{ ABD }$ の外接円との交点で B と異なるものを E とする。

　$\mathrm{ CE }\cdot \mathrm{ CB }=\myBox{アイ}$ であるから、$\mathrm{ BE }=\sqrt{\myBox{ウ}}$ である。

　$\triangle \mathrm{ ACE }$ の重心を G とすると、$\displaystyle \mathrm{ AG }=\frac{\myBox{エオ}}{\myBox{カ}}$である。

　AB と DE の交点を P とすると\[ \frac{\mathrm{ DP } }{\mathrm{ EP } } = \frac{\myBox{キ}}{\myBox{ク}} \quad \cdots ①\]である。

　$\triangle \mathrm{ ABC }$ と $\triangle \mathrm{ EDC }$ において、点A、B、D、E は同一円周上にあるので $\angle \mathrm{ CAB } = \angle \mathrm{ CED } $ で、$\angle \mathrm{ C }$ は共通であるから\[\mathrm{ DE }=\myBox{ケ}\sqrt{\myBox{コ}} \quad \cdots ②\]である。

　①、②から、$\displaystyle \mathrm{ EP } = \frac{\myBox{サ}\sqrt{\myBox{シ}} }{\myBox{ス} }$である。

考え方

まずは、図を正しくかくところから始めましょう。参考図がないので自分でかくしかありませんが、はじめでつまづくと後に響いてしまいます。

はじめは、線分の積から何を使うか考えましょう。重心については、B が CE の中点になることから求めます。①は、図がきれいにかけていないと、少し気づきにくいかもしれません。

DE は相似から求めます。これらを組み合わせれば、最後を出すのもそれほど難しくありません。

解答編

問題

　$\triangle \mathrm{ ABC }$ において、$\mathrm{ AB }=\mathrm{ AC }=5$、$\mathrm{ BC }=\sqrt{5}$ とする。辺AC 上に点D を $\mathrm{ AD }=3$ となるようにとり、辺BC の B の側の延長と $\triangle \mathrm{ ABD }$ の外接円との交点で B と異なるものを E とする。

解説

この時点で、図は次のようになっています。

解答編つづき

問題

　$\mathrm{ CE }\cdot \mathrm{ CB }=\myBox{アイ}$ であるから、$\mathrm{ BE }=\sqrt{\myBox{ウ}}$ である。

解説

方べきの定理より、
\begin{eqnarray} \mathrm{ CE } \cdot \mathrm{ CB } &=& \mathrm{ CA } \cdot \mathrm{ CD }　\\ &=& \mathrm{ CA } \cdot (\mathrm{ AC } - \mathrm{ AD }) \\ &=& 5 \cdot (5-3) = 10 \end{eqnarray}となります。

ここで、$\mathrm{ BC }=\sqrt{5}$ なので、$\mathrm{ CE }=2\sqrt{5}$ となります。よって、$\mathrm{ BE }=\sqrt{5}$ となります。

解答

アイ：10
ウ：5

解答編つづき

問題

　$\triangle \mathrm{ ACE }$ の重心を G とすると、$\displaystyle \mathrm{ AG }=\frac{\myBox{エオ}}{\myBox{カ}}$である。

解説

先ほどの結果から、点B が EC の中点であることがわかります。よって、$\triangle\mathrm{ ACE }$ の重心G は、AB を2:1に内分する点になります。つまり、\[ \mathrm{ AG }=\mathrm{ AB }×2/3=10/3 \]となります。

解答

エオカ：103

解答編つづき

問題

　AB と DE の交点を P とすると\[ \frac{\mathrm{ DP } }{\mathrm{ EP } } = \frac{\myBox{キ}}{\myBox{ク}} \quad \cdots ①\]である。

解説

図はこのようになっています。

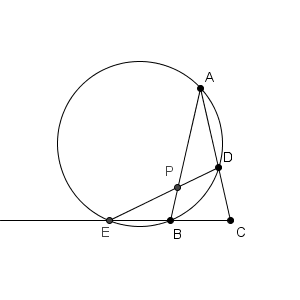
メネラウスの定理から
\begin{eqnarray} \frac{\mathrm{ BE } }{\mathrm{ CB } } \cdot \frac{\mathrm{ PD } }{\mathrm{ EP } } \cdot \frac{\mathrm{ AC } }{\mathrm{ DA } } &=& 1 \\[5pt] \frac{\sqrt{5} }{\sqrt{5} } \cdot \frac{\mathrm{ PD } }{\mathrm{ EP } } \cdot \frac{5}{3} &=& 1 \\[5pt] \frac{\mathrm{ DP } }{\mathrm{ EP } } &=& \frac{3}{5} \end{eqnarray}がわかります。

解答

キク：35

解答編つづき

問題

　$\triangle \mathrm{ ABC }$ と $\triangle \mathrm{ EDC }$ において、点A、B、D、E は同一円周上にあるので $\angle \mathrm{ CAB } = \angle \mathrm{ CED } $ で、$\angle \mathrm{ C }$ は共通であるから\[\mathrm{ DE }=\myBox{ケ}\sqrt{\myBox{コ}} \quad \cdots ②\]である。

解説

点E は $\triangle\mathrm{ ABD }$ の外接円上の点なので、A・B・D・E の4点は同一円周上にあります。なので、$\angle\mathrm{ CAB } = \angle\mathrm{ DEC }$ であることがわかります。

よって、三角形ABC と三角形EDC について、$\angle\mathrm{ CAB }=\angle\mathrm{ CED }$ で、$\angle\mathrm{ C }$ は共通であるから、相似であることがわかります。

三角形ABC は二等辺三角形だったので、三角形EDC も二等辺三角形。だから、$\mathrm{ DE }=\mathrm{ CE }=2\sqrt{5}$ となります。

解答

ケコ：25

解答編つづき

問題

　①、②から、$\displaystyle \mathrm{ EP } = \frac{\myBox{サ}\sqrt{\myBox{シ}} }{\myBox{ス} }$である。

解説

①は $\displaystyle \frac{\mathrm{ DP } }{\mathrm{ EP } } = \frac{3}{5}$ です。これから、$\displaystyle \frac{\mathrm{ DE } }{\mathrm{ EP } } = \frac{8}{5}$ がわかります。

また、②は$\mathrm{ DE }=2\sqrt{5}$ です。

この2つの式から、
\begin{eqnarray} \mathrm{ EP } &=& \mathrm{ DE } \cdot \frac{\mathrm{ EP } }{\mathrm{ DE } } \\[5pt] &=& 2\sqrt{5} \cdot \frac{5}{8} \\[5pt] &=& \frac{ 5 \sqrt{5} }{ 4 } \end{eqnarray}となります。