【標準】媒介変数表示と面積と積分（サイクロイド）

🕒 2018/12/22 🔄 2023/05/01

ここではサイクロイドを例にして、媒介変数表示で表された曲線で囲まれた部分の面積を、積分を使って求める方法を見ていきます。

📘 目次

サイクロイドと面積

例題

$a\gt 0$, $0\leqq \theta\leqq 2\pi$ とする。このとき、サイクロイド
\begin{eqnarray} x &=& a(\theta-\sin\theta) \\[5pt] y &=& a(1-\cos\theta) \\[5pt] \end{eqnarray}と $x$ 軸とで囲まれた部分の面積を求めなさい。

サイクロイドとは、【基本】サイクロイドと媒介変数表示で見た曲線ですが、いったん、そのことは忘れて、曲線の概形を考えることにしましょう。

$x$ を $\theta$ で微分すると、\[ a(1-\cos\theta) \]となるので、 $0\lt \theta\lt 2\pi$ 範囲では正ですね。なので、 $\theta$ が増加するにつれて、 $x$ も増加していく、ということがわかります。

$y$ は微分するまでもないですね。 $0\leqq \theta\leqq \pi$ の間は単調増加、 $\pi\leqq \theta\leqq 2\pi$ の間は単調減少であることがわかります。

以上のことを組み合わせると、 $\theta$ が増えると、ずっと右に移動しながら、 $\pi$ までは上へ、 $\pi$ からは下へ行くことがわかります。 $\theta=0,\pi,2\pi$ とすると $y=0,2a,0$ となり、山のような形になることがわかりますね。

以上のことから概形を予想することはできますが、正解は次のようになります。

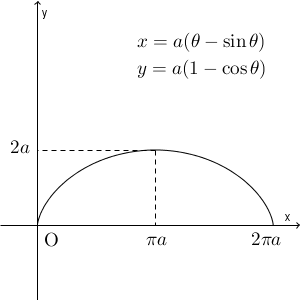
この曲線と $x$ 軸で囲まれた部分の面積を求めればいいんですね。

何を何で積分すればいいかがわかりにくいですね。今までどうやってたかを思い出してみましょう。【基本】x軸とで囲まれた部分の面積と積分で見たように、 $a\leqq x\leqq b$ のときに $f(x)\geqq 0$ であれば、 $y=f(x)$ , $x$ 軸、 $x=a$, $x=b$ で囲まれた部分の面積は\[ \int_a^b f(x)dx \]で求められるのでした。

今の場合、 $x$ について $0$ から $2\pi a$ まで積分するんだろうな、ということはわかると思いますが、 $f(x)$ にあたるものがわからないですね。 $y=f(x)$ の形で書けないので、仕方なく\[ \int_0^{2\pi a} y dx \]と書くしかありません。

ところが、そもそも、 $x,y$ は $\theta$ の式で書けるのだから、この時点で、置換積分を行えばいいですね。 $x=a(\theta-\sin\theta)$ より、 $dx$ は\[ a(1-\cos\theta) d\theta \]に置き換えればいいですね。積分区間は、
\begin{array}{c|ccc} x & 0 & \cdots & 2\pi a \\ \hline \theta & 0 & \cdots & 2\pi \\ \end{array}だから、面積は \begin{eqnarray} & & \int_0^{2\pi a} y dx \\[5pt] &=& \int_0^{2\pi} a(1-\cos\theta) \cdot a(1-\cos\theta) d\theta \\[5pt] &=& a^2 \int_0^{2\pi} (1-2\cos\theta+\cos^2\theta) d\theta \\[5pt] &=& a^2 \int_0^{2\pi} \left(1-2\cos\theta+\frac{1+\cos 2\theta}{2}\right) d\theta \\[5pt] &=& a^2 \Big[ \theta-2\sin\theta+\frac{\theta}{2}+\frac{\sin 2\theta}{4} \Big]_0^{2\pi} \\[5pt] &=& a^2(2\pi-0+\pi+0) \\[5pt] &=& 3\pi a^2 \\[5pt] \end{eqnarray}と求められます。これが答えです。

媒介変数で表示された曲線が絡んだ面積を積分で求める場合には、図をかいてどのように積分すべきかを考え、置換積分の計算を行う、というのが基本的な流れです。