【標準】楕円で囲まれた部分の面積と積分
ここでは、楕円で囲まれた部分の面積を、積分を使って求める方法を見ていきます。
楕円で囲まれた部分の面積
【基本】楕円の焦点(焦点がx軸上)などで見た通り、例題にある式は楕円の方程式で、グラフは次のようになります。
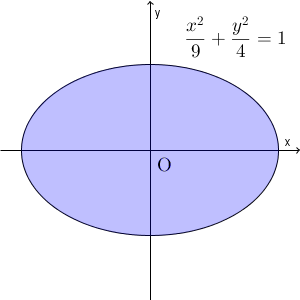
この囲まれた部分の面積を求める問題です。
今まで、曲線と $x$ 軸の間や、曲線と曲線の間の部分の面積を求める方法は、【基本】x軸とで囲まれた部分の面積と積分や、【基本】2曲線間の面積と積分の復習などで見てきました。これらを応用して、今の例題を考えてみましょう。
「曲線で囲まれた部分」と考えると少し思いつきにくいですが、「x 軸より上の部分」と「x 軸より下の部分」にはさまれた部分だと考えれば、「2曲線間の面積」を求めればいいことがわかるでしょう。上側の曲線は\[ y=2\sqrt{1-\dfrac{x^2}{9} } \]と書け、下側はこれにマイナスをつけたものなので、
\begin{eqnarray}
& &
\int_{-3}^3 \left\{2\sqrt{1-\dfrac{x^2}{9} }-\left(-2\sqrt{1-\dfrac{x^2}{9} }\right)\right\} dx \\[5pt]
&=&
2\int_{-3}^3 2\sqrt{1-\dfrac{x^2}{9} } dx \\[5pt]
\end{eqnarray}となることがわかります。この式は、よく考えてみると、当たり前の変形です。この楕円は $x$ 軸について対称なので、上側の曲線と $x$ 軸とで囲まれる部分の面積を2倍したものと楕円の面積が等しくなる、という意味の式だからです。
さらに、楕円は $y$ 軸についても対称なのだから、次のように変形できます。
\begin{eqnarray}
& &
2\int_{-3}^3 2\sqrt{1-\dfrac{x^2}{9} } dx \\[5pt]
&=&
4\int_0^3 2\sqrt{1-\dfrac{x^2}{9} } dx \\[5pt]
\end{eqnarray}楕円の右上部分と、 $x$ 軸、 $y$ 軸で囲まれた部分を4倍すれば、楕円の面積になる、ということです。図形的に考えれば当たり前です。なお、上の変形は、【標準】偶関数と奇関数の定積分で見た、偶関数の積分を変形したとも考えられます。
こうして、この楕円の面積は
\begin{eqnarray}
& &
4\int_0^3 2\sqrt{1-\dfrac{x^2}{9} } dx \\[5pt]
&=&
\frac{8}{3} \int_0^3 \sqrt{9-x^2} dx \\[5pt]
\end{eqnarray}を計算すればよく、【標準】定積分の置換積分(三角関数:cosθやsinθを使う)で見たように、 $x=3\sin\theta$ と置けば
\begin{eqnarray}
& &
\frac{8}{3} \int_0^3 \sqrt{9-x^2} dx \\[5pt]
&=&
\frac{8}{3} \int_0^{\frac{\pi}{2} } 3\cos\theta (3\cos\theta) d\theta \\[5pt]
&=&
24 \int_0^{\frac{\pi}{2} } \cos^2\theta d\theta \\[5pt]
&=&
24 \int_0^{\frac{\pi}{2} } \frac{1+\cos 2\theta}{2} d\theta \\[5pt]
&=&
24 \Big[ \frac{\theta}{2}+\frac{\sin 2\theta}{4} \Big]_0^{\frac{\pi}{2} } \\[5pt]
&=&
24 \cdot \frac{\pi}{4} \\[5pt]
&=&
6\pi
\end{eqnarray}と求められます。
ただ、実はこの計算も、まじめに計算する必要はありません。というのも、\[ \int_0^3 \sqrt{9-x^2} dx \]は、意味を考えればすぐに求められるからです。被積分関数がどんな曲線を表しているかを考えてみましょう。\[ y=\sqrt{9-x^2} \]とすると、 $x^2+y^2=9$ なので、これは、原点を中心とした半径3の円の一部を表しています。なので、 $0$ から $3$ まで積分するということは、この円の右上の部分である $\dfrac{1}{4}$ を表しているので、\[ \frac{3^2}{4}\pi \]となり、これを $\dfrac{8}{3}$ 倍して、楕円の面積が $6\pi$ とあることがわかります。【標準】定積分の置換積分(三角関数:cosθやsinθを使う)の中盤でも、似たような議論をしているので見てみましょう。
楕円で囲まれた部分の面積(一般の場合)
$a\gt 0$, $b\gt 0$ のとき、楕円 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$ の面積を求めてみましょう。これは、先ほど見た通り、楕円の右上部分を考えればいいですね。 $x,y\geqq 0$ の部分と、 $x$ 軸、 $y$ 軸で囲まれた部分を4倍すればいいです。よって、
\begin{eqnarray}
& &
4\int_0^a b\sqrt{1-\dfrac{x^2}{a^2} } dx \\[5pt]
&=&
\frac{4b}{a}\int_0^a \sqrt{a^2-x^2} dx \\[5pt]
\end{eqnarray}を計算すればいいですが、このうち、最後の式の積分は、原点を中心とした半径 $a$ の円の面積の $\dfrac{1}{4}$ なので、この計算結果は $\dfrac{\pi a^2}{4}$ となります。よって、楕円の面積は\[ \frac{4b}{a}\times \frac{\pi a^2}{4}=\pi ab \]となります。
【基本】楕円の方程式と円の方程式で見たように、楕円は円を縦に拡大・縮小したものであることを考えれば、\[ \pi a^2\times\frac{b}{a} \]となることは当たり前のようにも感じられますね。
おわりに
ここでは、曲線で囲まれた部分の面積を求める問題として、楕円で囲まれた部分の面積を求める問題を見ました。図形的に考えることで、計算を少し簡略化することができましたね(右上部分の4倍、で求められました)。積分を行う前に、図形的に考えることで計算量を減らせることもありますので、その点にも注意しながら今後もいろいろな問題を見ていきましょう。





