🏠 Home / 数学III / 微分 / 微分と接線

【標準】通る点から接線の方程式を求める

🕒 2018/10/10 🔄 2023/06/26

ここでは、通る点が指定されている状況で、接線の方程式を求める問題を見ていきます。

📘 目次

通る点から接線の方程式を求める

例題

原点を通り、曲線 $y=\log x$ に接する直線の方程式を求めなさい。

【基本】微分と接線・法線の方程式で見たように、 $y=f(x)$ の $(a,f(a))$ での接線の方程式は\[ y-f(a)=f'(a)(x-a) \]で表すことができます。このことを利用して考えていきましょう。

接線の方程式は、接点での情報を使って表されます。今の例題では「原点を通る」ことがわかっていますが、まずは接点を考え、接線の方程式を考えてから、「この接線が原点を通るのはどういうときか？」という順番で考えていきます。

通る点よりも、接点のほうがわかることが多いので、接点を出発点にしたほうが考えやすくなることが多いです。

$f(x)=\log x$ とおき、接点を $(a,f(a))$ とします $(a\gt 0)$ 。 $f'(x)=\dfrac{1}{x}$ なので、この点で $y=f(x)$ に接する直線の方程式は\[ y-\log a=\frac{1}{a}(x-a) \]と表すことができます。これが「原点を通る」という条件から、 $a$ の値を求めていきます。

$(x,y)=(0,0)$ を代入すると
\begin{eqnarray} 0-\log a &=& \frac{1}{a}(0-a) \\[5pt] \log a &=& 1 \\[5pt] a &=& e \\[5pt] \end{eqnarray}となります。よって、接点は $(e,1)$ であることがわかります。

接点がわかったので、接線の方程式は
\begin{eqnarray} y-1 &=& \frac{1}{e}(x-e) \\[5pt] y &=& \frac{1}{e}x \\[5pt] \end{eqnarray}と求めることができます。これが答えとなります。

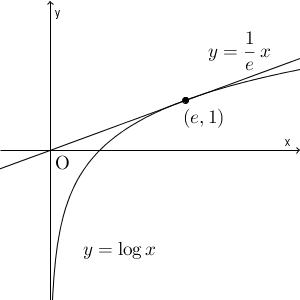
グラフは上のようになります。

なお、ここで見たように「この点を通る接線の方程式を求めなさい」という問題は、「この点からこの曲線に引いた接線の方程式を求めなさい」という形で出題されることもあります（参考：【標準】ある点から引いた接線（三次関数））。表現が違うだけで、趣旨は同じです。

放物線のときと何が違うか

上の例題では、 $y=\log x$ の場合でしたが、過去に、右辺が二次関数となっている問題を解いたことがある人もいるでしょう。

「原点を通り、 $y=ax^2+bx+c$ に接する直線」であれば、接点ではなく接線の方から攻める方法もあります。つまり、接線の方程式を $y=mx$ とおいて、 $m$ を求める、という方針です。このとき\[ ax^2+bx+c=mx \]という二次方程式は、判別式が $0$ となるので、この条件から傾きが求められます。

では、上の例題も同じように、「 $y=mx$ とおいてから解くことはできないだろうか？」と考える人もいるかもしれません。しかし、この方針は難しいでしょう。

二次関数・二次方程式の場合は、「接する」を「判別式が $0$ 」と言い換えることができます。放物線と直線の場合、共有点の数はつねに2個以下であり、1個の場合に「接する」というのでした。なので、二次方程式の解が1個となる場合を考えればいいわけです。二次方程式には解の公式があるので、「判別式が $0$ 」と言い換えることができます。

ただ、一般の場合には、接するからといって共有点が1個とは限らない（三次関数のときを思い出しましょう）し、共有点の数がわかったところで解の公式はなく、判別式もありません。なので、二次方程式のときのようにはいきません。

一般の関数の場合、接線というのは、「接点での微分係数が同じ直線」のことなので、接点の情報から考えていくことが基本的な方針となります。