【標準】円と直線が交わる条件

ここでは、座標平面上で、円と直線が2点で交わる条件について見ていきます。2通りの方法を紹介します。

円と直線が交わる条件

図は次のようになっています。 k が変わると、直線が上下します。

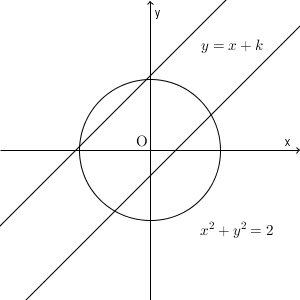
直線が上下することに着目すると、2点で交わるのは、円の左上で接するときと、右下で接するときの間、が求める範囲になるだろう、と予想できますね。このような範囲を求めてみましょう。

まず、真っ先に思いつくのは、2つの方程式から y を消し、 x の二次方程式にしてから、判別式を使う方法でしょう。方程式を満たす x 座標が2つあるということと、異なる2点で交わることは同じですからね。

しかし、共有点の個数を考えるだけなら、円の中心と直線との距離に着目したほうが楽になることが多いです。

以下では、これら2つの方法で解いてみます。

円の中心からの距離に注目した解き方

【基本】円と直線の共有点（中心からの距離に注目）でも見ましたが、円と直線が2点で交わる、ということは、円の中心と直線との距離が、円の半径よりも短い、ということです。ここに着目して解いてみましょう。

円の中心 $(0,0)$ と直線 $y=x+k$ との距離を考えてみましょう。この直線は $x-y+k=0$ とも書けるので、【基本】原点と直線との距離で見た内容から、距離は\[ \frac{|k|}{\sqrt{1^2+(-1)^2} }=\frac{|k|}{\sqrt{2} } \]となります。

これが半径よりも短くなる条件を求めればいいので、
\begin{array}{c} \dfrac{|k|}{\sqrt{2} } \lt \sqrt{2} \\[5pt] |k| \lt 2 \\[5pt] -2 \lt k \lt 2 \\[5pt] \end{array}となります。これが答えです。

点と直線の距離が簡単に求められるので、それほど計算量は多くなりません。

方程式に注目した解き方

続いて、方程式の解の個数に注目した解き方で考えてみましょう。

直線の方程式 $y=x+k$ を、円の方程式 $x^2+y^2=2$ に代入します。
\begin{eqnarray} x^2+y^2 &=& 2 \\[5pt] x^2+(x+k)^2 &=& 2 \\[5pt] 2x^2+2kx+k^2-2 &=& 0 \\[5pt] \end{eqnarray}

異なる2点で交わることと、上の方程式が異なる2つの解を持つこととは同値なので、判別式が正になる条件を求めればいいですね。この条件を計算すると
\begin{eqnarray} (2k)^2-4\cdot2\cdot(k^2-2) & \gt & 0 \\[5pt] k^2-2k^2+4 & \gt & 0 \\[5pt] k^2-4 & \lt & 0 \\[5pt] (k-2)(k+2) & \lt & 0 \\[5pt] -2 \lt & k \lt 2 \\[5pt] \end{eqnarray}となります。当たり前ですが、1つ目の解き方と同じ答えになりました。

二次式に代入したり、判別式を計算したり、と、少し計算量が多いですね。こちらの解き方に慣れている人もいるかもしれませんが、計算量から考えると、1つ目の解き方もマスターしたほうがいいと思います。

図形的に考える

2点で交わるのは、接するときを基準に考えればいいのではないか、という発想もあるでしょう。接するときの図をかいてみると、次のようになります。

直線が円に接しているとき、円の中心と接点とを結んだ線は直線と垂直になります。

このことと、直線の傾きが $1$ であることを考えれば、原点、接点、直線と y 軸との交点、の3点をつないでできる三角形は、直角二等辺三角形です。半径は $\sqrt{2}$ なので、接するときの切片は、 $2$ であることがわかります。下側も同じように考えて、右下で接するときの切片は $-2$ となることがわかります。

この間であれば、円と直線の共有点は2点となり、それ以外で2点となることはありません。よって\[ -2\lt k \lt 2 \]であることがわかります。

ただ、この解き方は、この問題だから解ける方法です。 k を動かすと、直線がどう動くかがわかりやすいこと、直線の傾きが扱いやすい値に固定されていること、などのおかげで解けますが、数字や設定が少し変わったら解けなくなる可能性があります。

なので、図形で考える方法は、「こういう考え方もある」と頭に入れておくだけにして、実際に問題を解くときには上で紹介した1つ目・2つ目の解き方で考えるのがいいでしょう。図形的に考える方法は、答えや解き方を推測したり、検算の目的で使うことが多いです。

おわりに

ここでは、円と直線が交わる条件、共有点が2点となる条件を見てきました。距離に注目する方法、方程式に注目する方法を紹介しました。距離に注目するほうが計算が楽になることが多いので、こちらの方法も使えるようになっておきましょう。