🏠 Home / 数学II / 図形と方程式 / 円と方程式

【標準】定点を通る円

🕒 2017/08/21 🔄 2023/05/01

ここでは、円を動かしたときに、ある定点を通るような場合を見ていきます。

📘 目次

定点を通る円

例題

円 $x^2+kx+y^2+ky-2k-10=0$ は、 k の値に関わらず、ある定点を通る。その定点の座標を求めなさい。

本当に定点を通るのか、やってみましょう。

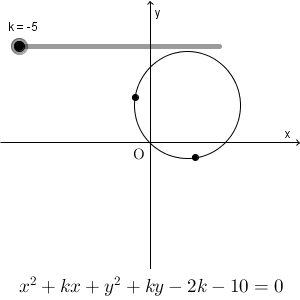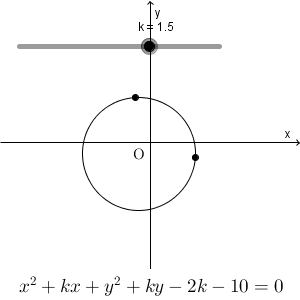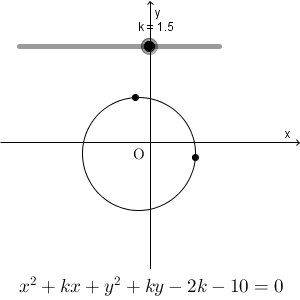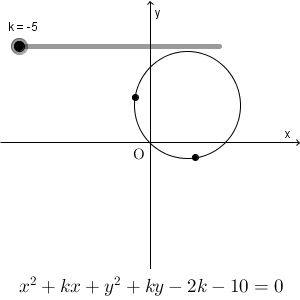
確かに通ってますね。2つの定点を通るようです。

k を動かしたときに、図形がある定点を通る、という問題は、他のページでも扱っています。「直線がある定点を通る」という問題を、【標準】定点を通る直線で扱っています。

基本的な考え方は同じです。「 k の値に関わらず、ある定点を通る」ということは、「 k の値に関わらず、等式が成り立つ」ということなので、 k に関する恒等式だと考えればいいわけですね（参考：【基本】恒等式）。

まずは、 k について、整理しましょう。
\begin{eqnarray} x^2+kx+y^2+ky-2k-10 &=& 0\\[5pt] (x^2+y^2-10)+k(x+y-2) &=& 0\\[5pt] \end{eqnarray}となります。これが k についての恒等式になることは、各カッコの中が $0$ になることと同値です。2つ目のカッコから\[ y=-x+2 \]が得られるので、これを1つ目のカッコに関する条件に代入して \begin{eqnarray} x^2+(-x+2)^2-10 &=& 0 \\[5pt] x^2+x^2-4x+4-10 &=& 0 \\[5pt] x^2-2x-3 &=& 0 \\[5pt] (x-3)(x+1) &=& 0 \\[5pt] x &=& 3,-1 \end{eqnarray}が得られます。 $y=-x+2$ に代入すれば、通る定点の座標は、 $(3,-1)$, $(-1,3)$ となることがわかります。これが答えです。

なんの円の集まりだったのか

【標準】定点を通る直線のときも考えましたが、 k を動かしたときに得られる円というのは、どんな円だったのかを考えてみましょう。

恒等式だと考えたときに、円の方程式を次のように変形しましたね。\[ (x^2+y^2-10)+k(x+y-2)=0 \]k に関する恒等式だから、2つのカッコの中身がともに $0$ になるときを考えました。ということは、見方を変えれば、上の例題で求めた定点は、円 $x^2+y^2=10$ と直線 $y=-x+2$ の両方を通ることがわかります。

つまり、上の例題に出てきた円 $x^2+kx+y^2+ky-2k-10=0$ は、円 $x^2+y^2=10$ と直線 $y=-x+2$ の共有点を通る円の集まりだったわけですね。

これは、逆にいえば、「ある円とある直線の共有点を通る円を求める」ときに、「共有点の座標を求めて、それらの点を通る円を求める」という手順をとる必要がないことを表しています。直線の方程式を k 倍して円の方程式に足せば、「共有点を通る円の方程式」が出来上がるわけです。これにより、計算がすごく楽になります。この考え方を使った問題は、また別の機会に取り上げます。