🏠 Home / 数学B / 数列 / 漸化式

【応用】ハノイの塔と漸化式

🕒 2018/03/21 🔄 2023/05/01

ここでは、漸化式を作るところから考える問題を見ていきます。例として、ハノイの塔というゲームを扱います。

📘 目次

ハノイの塔

ハノイの塔とは、次のようなゲームです。

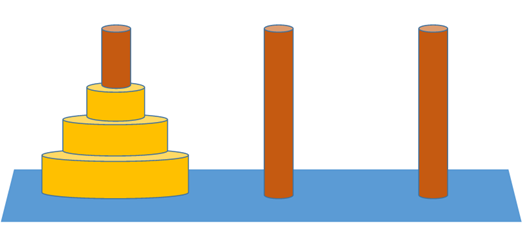
地面にくっついている3本の細い棒と、円板を使います。円板の中央には穴が開いており、棒が通るようになっています。円板の大きさはすべて異なり、一番はじめは、すべて左の棒にあり、大きい方から順に積みあがっています。

ハノイの塔は、以下のルールを守りながら、すべての円板を一番右の棒に移動させるゲームです。

1回の操作で、1枚の円板を移動させる
円板は、どこかの棒に移動させる（棒以外の場所に置くのはダメ）
小さい円板の上に大きな円板を乗せることはできない

例えば、円板が1枚なら、1回でおしまいですね。2枚なら、「1枚目を中央へ、2枚目を右端へ、1枚目を右端へ」という3回で移動することができます。

3枚の場合はもう少し多くなります。「1枚目を右端へ、2枚目を中央へ、1枚目を中央へ、3枚目を右端へ、1枚目を左端へ、2枚目を右端へ、1枚目を右端へ」となり、7回で移動することができます。

ここで挙げた通りにすれば、最小回数で右の棒に移動させることができます。

では、円板が10枚の場合、最小で何回移動すればいいでしょうか。また、 n 枚のときはどうでしょうか。

やってみるとわかりますが、10枚になるとすごく大変です。1000回を超えてしまいます。 n 枚に至っては、「実際にやって答えを出す」ということがそもそもできません。

漸化式をつくろう

さて、ハノイの塔での最小移動回数を考えましょう。

円板が n 枚のときをいきなり考えるのは大変です。しかし、【基本】漸化式以降で学んできた漸化式を使えば、道が開けてきます。

いきなり一般的な状況を考えるのは難しくても、「n 番目と $(n+1)$ 番目の関係」に限定すれば、考えやすくなることがあります。今の場合、このテクニックが使えるので見てみましょう。

円板が $n$ 枚のときの最小移動回数を $a_n$ としましょう。そして、これに関する漸化式を作ることを考えましょう。そうすれば、あとは漸化式を解くだけ、となります（現時点では、その漸化式が解けるかどうかはなぞですが）。

漸化式では、「n 番目と $(n+1)$ 番目の関係」を考えないといけません。それでは、円板が $(n+1)$ 枚になったときのことについて考えましょう。

円板が $n$ 枚のときと $(n+1)$ 枚のときとで、何が違うかというと、もちろん $(n+1)$ 枚目の円板が追加されたことですね。ここが違うので、この円板に注目しましょう。

この $(n+1)$ 枚目の円板が動くとき、上にある $n$ 枚の円板はどこかに移動していないといけないですね。また、 $(n+1)$ 枚目の円板は右端に移動しないといけません。ということは、 $(n+1)$ 枚目の円板が移動するとき、次のような状況になっていることがわかります。

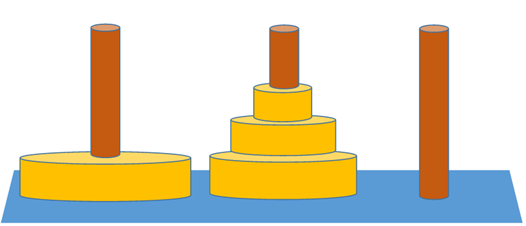
真ん中に $n$ 枚積みあがっていて、一番下の円板が左端から右端へ移動する、ということですね。この「真ん中に $n$ 枚積み上げる」のに必要な最小移動回数は、よくよく考えると $a_n$ 回です。というのも、 $n$ 枚の円板をすべて右端に移動させるのも、すべて中央に移動させるのも同じ回数になるからですね。

$(n+1)$ 枚目の円板を右端に移動した後は、 $n$ 枚の円板を中央から右端に移動しなければいけません。この最小回数は、やはり $a_n$ 回ですね。

以上から、 $(n+1)$ 枚の円板を左端から右端へ移動する最小回数は、

$n$ 枚の円板を左端から中央へ移動（ $a_n$ 回）
$(n+1)$ 枚目の円板を左端から右端へ移動（ $1$ 回）
$n$ 枚の円板を中央から右端へ移動（ $a_n$ 回）

となります。このことから、\[ a_{n+1}=2a_n+1 \]となることがわかります。この式は、【基本】漸化式（特殊解型）で出てきています。特性方程式\[ p=2p+1 \]を解いて $p=-1$ が得られるので、\[ a_{n+1}+1=2(a_n+1) \]となります。これより、\[ a_n+1=2^{n-1}(a_1+1) \]が得られます。円板が1枚のときは1回なので $a_1=1$ だから\[ a_n=2^n-1 \]となります。

つまり、 $n$ 枚の円板があるときは、最小移動回数は $(2^n-1)$ 回になることがわかります。10枚のときは、1023回ですね。