【応用】チェバの定理の逆
ここでは、チェバの定理の逆について見ていきます。教科書ではまったく紹介されていないか、証明なしで内容だけの紹介にとどまっているかもしれません。大学入試でもそんなに使う場面は多くないです。
チェバの定理の逆
【応用】チェバの定理とメネラウスの定理でも見た通り、辺の延長線上に交点がある場合もOKとしたバージョンのチェバの定理は、次のような内容です。
このとき、次の等式が成り立つ。\[ \frac{\mathrm{AR}}{\mathrm{RB}} \cdot \frac{\mathrm{BP}}{\mathrm{PC}} \cdot \frac{\mathrm{CQ}}{\mathrm{QA}}= 1 \]
実は、チェバの定理の逆も成り立ちます。ただ、少し注意が必要です。
一般的に、命題の「逆」とは、仮定と結論を入れ替えたものを言いますが、チェバの定理の場合は、仮定と結論を入れ替えるだけでは成り立ちません。条件を追加する必要があるため、一般的な「命題の逆」とは異なります。
そもそも、チェバの定理の仮定が何かがわかりづらいですね。最後に出てくる式\[ \frac{\mathrm{AR}}{\mathrm{RB}} \cdot \frac{\mathrm{BP}}{\mathrm{PC}} \cdot \frac{\mathrm{CQ}}{\mathrm{QA}}= 1 \]これが結論であることはわかりやすいですが、仮定にあたる部分(言い換えると、「チェバの定理の逆」の結論にあたる部分)はなんでしょうか。これは、答えを書いてしまうと、「点 $\mathrm{O}$ の存在」です。つまり、3直線 $\mathrm{AP,BQ,CR}$ が1点で交わること、です。
以上を踏まえると、「チェバの定理の逆」のおおざっぱな内容は以下の通りです(まだ正しくはないですが、最終的に正しいものに修正します)。
「$\triangle \mathrm{ABC}$ について、直線 $\mathrm{BC,CA,AB}$ 上に点 $\mathrm{P,Q,R}$ をとる。このとき、$\frac{\mathrm{AR}}{\mathrm{RB}} \cdot \frac{\mathrm{BP}}{\mathrm{PC}} \cdot \frac{\mathrm{CQ}}{\mathrm{QA}}= 1$ が成り立てば、3直線 $\mathrm{AP,BQ,CR}$ が1点で交わる。」
これはチェバの定理の逆っぽい内容ですが、実は正しくありません。そもそも、「3つの積が $1$ になる」というのは、メネラウスの定理の結論にもなっていましたね。つまり、「3つの積が $1$ になる」という条件だけでは、「3直線 $\mathrm{AP,BQ,CR}$ が1点で交わる」というケースだけではなく、「3点 $\mathrm{P,Q,R}$ が一直線上にある」ケース(「メネラウスの定理の逆」に対応)もありえるのです。
ではどういう条件をつければいいかというと、それが、【応用】チェバの定理とメネラウスの定理で見た内容につながってきます。3点 $\mathrm{P,Q,R}$ のうち、辺上にあるのはいくつあるか、というポイントです。このリンク先で見たように、辺上にあるのが1個または3個のときがチェバの定理に対応するので、チェバの定理の逆については、これを仮定する必要があります。
さらに面倒なことに、これだけではまだ足りません。「3つの積が $1$ 」をクリアし、「$\mathrm{P,Q,R}$ のうち、辺上にあるのは1個または3個」もクリアしていても、3直線が1点で交わらないケースがあります。それが、以下のようなケースです。
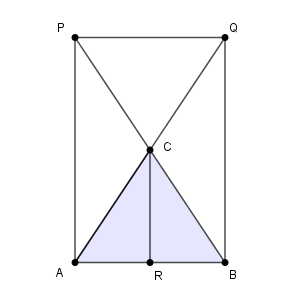
上の図で、四角形 $\mathrm{PABQ}$ は長方形で、 $\mathrm{R}$ は線分 $\mathrm{AB}$ の中点です。このとき $\mathrm{C}$ は対角線の中点になるので\[ \frac{\mathrm{AR}}{\mathrm{RB}} \cdot \frac{\mathrm{BP}}{\mathrm{PC}} \cdot \frac{\mathrm{CQ}}{\mathrm{QA}}=\frac{1}{1} \cdot \frac{2}{1} \cdot \frac{1}{2}=1 \]が成り立ちます。また、 $\mathrm{P,Q,R}$ のうち、辺上にあるのは1個です。しかし、3直線 $\mathrm{AP,BQ,CR}$ は1点では交わりません。3直線は互いに平行だからです。
なので、「互いに平行ではない」という条件も必要です。
まとめると、チェバの定理の逆は、次のような内容となります。
このとき、次の等式\[\frac{\mathrm{AR}}{\mathrm{RB}} \cdot \frac{\mathrm{BP}}{\mathrm{PC}} \cdot \frac{\mathrm{CQ}}{\mathrm{QA}}= 1 \]が成り立てば、3直線 $\mathrm{AP,BQ,CR}$ は1点で交わる。
もとの命題にはなかったものが追加されているため、いわゆる「命題の逆」とは異なるのですが、これを「チェバの定理の逆」といいます。3直線が1点で交わることを証明したいときに、この「チェバの定理の逆」が使われることがあります。
ちなみに、もし、点 $\mathrm{P,Q,R}$ がすべて辺の上にあるという状況なら、3直線 $\mathrm{AP,BQ,CR}$ が互いに平行になることはないので、この条件は考える必要はなくなります。
また、もとのチェバの定理には、点 $\mathrm{O}$ は辺上にもその延長線上にもないことを仮定していました。しかし、チェバの定理の逆にはそれに対応する文言はありません。これは、\[ \frac{\mathrm{AR}}{\mathrm{RB}} \cdot \frac{\mathrm{BP}}{\mathrm{PC}} \cdot \frac{\mathrm{CQ}}{\mathrm{QA}}= 1 \]が成り立つという条件の中に、暗に「点 $\mathrm{O}$ は辺上にもその延長線上にもないこと」が含まれているからです。もしそうなら、線分の長さが $0$ になるものがあるので、積が $1$ にはなりません。
チェバの定理の逆の証明
チェバの定理の逆の証明には、同一法という手法がよく使われます。高校数学では、あまり見かけない手法です。この手法については、証明の後に説明します。
さて、まず、わかりやすいように、点 $\mathrm{P}$ は辺 $\mathrm{BC}$ 上にあるとします。仮定から、 $\mathrm{Q,R}$ は、どちらも辺上か、どちらも辺の延長線上にあるか、のどちらかです。
次に、直線 $\mathrm{BQ,CR}$ の交点を $\mathrm{O}$ とし、直線 $\mathrm{AO,BC}$ の交点を $\mathrm{P}'$ とします。点 $\mathrm{Q,R}$ の位置より、点 $\mathrm{P'}$ は辺 $\mathrm{BC}$ 上にあることがわかります。

点 $\mathrm{P'}$ が辺 $\mathrm{BC}$ 上にあることをもう少し詳しく
もし、点 $\mathrm{P'}$ が辺 $\mathrm{BC}$ 上にないとしましょう。次のように、辺 $\mathrm{BC}$ の $\mathrm{B}$ 側の延長線上に点 $\mathrm{P'}$ があるとしましょう。
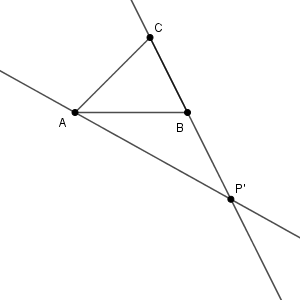
直線 $\mathrm{BQ,CR}$ の交点 $\mathrm{O}$ は直線 $\mathrm{AP'}$ 上にあります。これを、次のように3つの場合に分けて考えてみます。
まず、$\mathrm{O}$ が線分 $\mathrm{AP'}$ の $\mathrm{A}$ 側の延長線上にある場合を考えます。
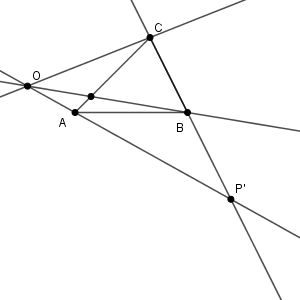
この場合、$\mathrm{BO}$ は辺 $\mathrm{AC}$ と交わりますが、$\mathrm{CO}$ は辺 $\mathrm{AB}$ とは交わりません。なので、「$\mathrm{Q,R}$ は、どちらも辺上か、どちらも辺の延長線上にあるか、のどちらか」という条件を満たしません。
次に、$\mathrm{O}$ が線分 $\mathrm{AP'}$ 上にある場合を考えます。
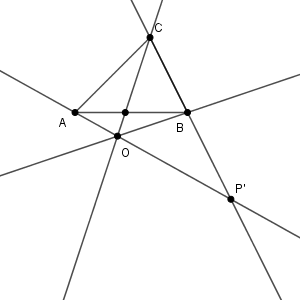
この場合、$\mathrm{BO}$ は辺 $\mathrm{AC}$ と交わりませんが、$\mathrm{CO}$ は辺 $\mathrm{AB}$ とは交わります。なので、「$\mathrm{Q,R}$ は、どちらも辺上か、どちらも辺の延長線上にあるか、のどちらか」を満たしません。
最後に、$\mathrm{O}$ が線分 $\mathrm{AP'}$ の $\mathrm{P'}$ 側の延長線上にある場合を考えます。
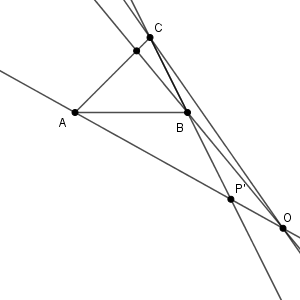
この場合、$\mathrm{BO}$ は辺 $\mathrm{AC}$ と交わりますが、$\mathrm{CO}$ は辺 $\mathrm{AB}$ とは交わりません。なので、この場合も条件を満たしません。
以上から、「$\mathrm{Q,R}$ は、どちらも辺上か、どちらも辺の延長線上にあるか、のどちらか」という条件から、点 $\mathrm{P'}$ が辺 $\mathrm{BC}$ の延長線上にはないことがわかります($\mathrm{C}$ 側にあるときも同じようにすればいいです)。よって、点 $\mathrm{P'}$ が辺 $\mathrm{BC}$ 上にあることがわかります。
さて、一旦、 $\mathrm{P}$ のことは忘れて、 $\mathrm{P}'$ について考えます。ここで、チェバの定理を使います。チェバの定理の逆を示している途中ですが、チェバの定理自体はすでに示しているので、使っても問題ありません。チェバの定理から、次の式が成り立ちます。\[ \frac{\mathrm{AR}}{\mathrm{RB}} \cdot \frac{\mathrm{BP'}}{\mathrm{P'C}} \cdot \frac{\mathrm{CQ}}{\mathrm{QA}}= 1 \]また、仮定から、次が成り立ちます。\[ \frac{\mathrm{AR}}{\mathrm{RB}} \cdot \frac{\mathrm{BP}}{\mathrm{PC}} \cdot \frac{\mathrm{CQ}}{\mathrm{QA}}= 1 \]この2つから、\[ \mathrm{BP:PC=BP':P'C} \]となります。点 $\mathrm{P,P'}$ はどちらも辺 $\mathrm{BC}$ 上の点だったので、この2点は同じ点であることがわかります。
直線 $\mathrm{AP'}$ が点 $\mathrm{O}$ を通るので、直線 $\mathrm{AP}$ も点 $\mathrm{O}$ を通ることがわかり、3直線 $\mathrm{AP,BQ,CR}$ は1点で交わることが示せました。
このように、ある性質を持つものが1つしかない場合、AもBもその性質を持つなら、2つは同じものだ、ということを利用した証明方法を同一法といいます。上の証明の中では、当初は別物として扱っていた $\mathrm{P,P'}$ が、実は同じ点だった、ということを示しています。
チェバの定理の逆を使った例題
チェバの定理の逆を使うと、「3直線が1点で交わること」が簡単に示せる場合があります。
例えば、重心の存在が簡単に示せます(参考:【基本】三角形の重心)。三角形 $\mathrm{ABC}$ について、辺 $\mathrm{BC,CA,AB}$ の中点を $\mathrm{P,Q,R}$ としましょう。このとき
\[ \frac{\mathrm{AR}}{\mathrm{RB}} \cdot \frac{\mathrm{BP}}{\mathrm{PC}} \cdot \frac{\mathrm{CQ}}{\mathrm{QA}}=\frac{1}{1} \cdot \frac{1}{1} \cdot \frac{1}{1} =1 \]となるので、チェバの定理の逆から、3直線 $\mathrm{AP,BQ,CR}$ が1点で交わることがわかります。つまり、これだけで、3つの中線が1点で交わることが示せたことになります。
内心の存在も簡単に示せます(参考:【基本】三角形の内心)。それぞれの内角の二等分線と辺との交点を $\mathrm{P,Q,R}$ とします。内角の二等分線の性質から\[ \frac{\mathrm{BP}}{\mathrm{PC}}=\frac{\mathrm{BA}}{\mathrm{AC}} \]が成り立ちます。他も同様にすると、\[ \frac{\mathrm{AR}}{\mathrm{RB}} \cdot \frac{\mathrm{BP}}{\mathrm{PC}} \cdot \frac{\mathrm{CQ}}{\mathrm{QA}}=\frac{\mathrm{AC}}{\mathrm{CB}} \cdot \frac{\mathrm{BA}}{\mathrm{AC}} \cdot \frac{\mathrm{CB}}{\mathrm{BA}}=1 \]となるので、チェバの定理から3つの内角の二等分線は1点で交わることが示せました。
このように、3つの直線が1点で交わることを示すときに、チェバの定理の逆が使える場面があります。
おわりに
ここでは、チェバの定理の逆について見てきました。チェバの定理をそのまま逆にするだけではなく、条件がつくことに注意しましょう。重心や内心の存在の例で見た通り、チェバの定理の逆は、3直線が1点で交わることを示すときに使えることがあります。





