【基本】メネラウスの定理
ここでは、メネラウスの定理とその証明について見ていきます。
メネラウスの定理
三角形と直線について、以下で述べる、メネラウスの定理(Menelaus' theorem) が成り立ちます。
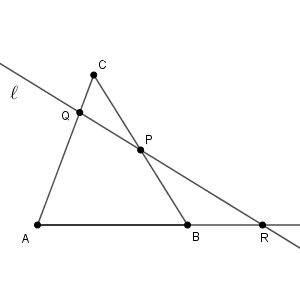
このとき、次の等式が成り立つ。\[ \frac{\mathrm{AR}}{\mathrm{RB}} \cdot \frac{\mathrm{BP}}{\mathrm{PC}} \cdot \frac{\mathrm{CQ}}{\mathrm{QA}}= 1 \]
式自体は、【基本】チェバの定理のときと同じですが、図が違いますね。ただ、点の並び方について、頂点・交点・頂点・交点… とたどっていけばいい、というのは同じです。

このようにたどりつつ、分子に「頂点→交点」、分母に「交点→頂点」を集めれば、\[ \frac{\mathrm{AR}}{\mathrm{RB}} \cdot \frac{\mathrm{BP}}{\mathrm{PC}} \cdot \frac{\mathrm{CQ}}{\mathrm{QA}}= 1 \]の式になります。
メネラウスの定理の証明
ここからは、メネラウスの定理の証明をしていきます。

まず、$\mathrm{B}$ を通り、直線 $\mathrm{AC}$ に平行な直線をひきます。この直線と直線 $\ell$ との交点を $\mathrm{T}$ としましょう。
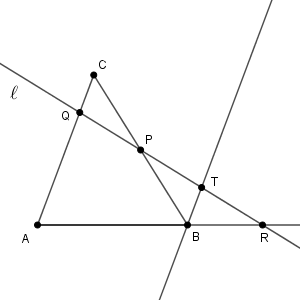
こうすると、 $\triangle \mathrm{ARQ}$ と $\triangle \mathrm{BRT}$ は相似なので、\[ \frac{\mathrm{AR}}{\mathrm{BR}} = \frac{\mathrm{AQ}}{\mathrm{BT}} \]が成り立ちます。
また、 $\triangle \mathrm{BTP}$ と $\triangle \mathrm{CQP}$ は相似なので、\[ \frac{\mathrm{BP}}{\mathrm{CP}} = \frac{\mathrm{BT}}{\mathrm{CQ}} \]が成り立ちます。
これらを使うと
\begin{eqnarray}
& &
\frac{\mathrm{AR}}{\mathrm{RB}} \cdot \frac{\mathrm{BP}}{\mathrm{PC}} \cdot \frac{\mathrm{CQ}}{\mathrm{QA}} \\[5pt]
&=&
\frac{\mathrm{AQ}}{\mathrm{BT}} \cdot \frac{\mathrm{BT}}{\mathrm{CQ}} \cdot \frac{\mathrm{CQ}}{\mathrm{QA}} \\[5pt]
&=&
1
\end{eqnarray}となるので、メネラウスの定理が成り立つことがわかります。
メネラウスの定理の例題
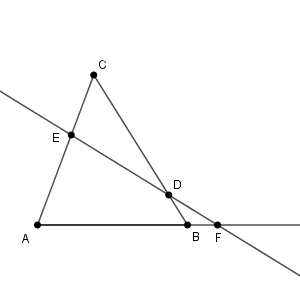
点の名前が違いますが、メネラウスの定理が使える形ですね。 $\triangle \mathrm{ABC}$ に直線 $\mathrm{EF}$ が刺さっていると考えると、頂点と交点を交互にたどっていけば\[ \mathrm{A,F,B,D,C,E,A} \]の順番になります。これを踏まえてメネラウスの定理を使うと
\begin{eqnarray}
\frac{\mathrm{AF}}{\mathrm{FB}} \cdot \frac{\mathrm{BD}}{\mathrm{DC}} \cdot \frac{\mathrm{CE}}{\mathrm{EA}} &=& 1 \\[5pt]
\frac{\mathrm{AF}}{\mathrm{FB}} \cdot \frac{1}{4} \cdot \frac{2}{3} &=& 1 \\[5pt]
\frac{\mathrm{AF}}{\mathrm{FB}} &=& 6 \\[5pt]
\end{eqnarray}となるので、 $\mathrm{AF:FB}=6:1$ と求められます。
では、次の $\mathrm{FD:DE}$ はどのように求めるでしょうか。これもメネラウスの定理を使うのですが、今度は見方を変える必要があります。
$\mathrm{FD:DE}$ を含む形になるように、 $\triangle \mathrm{AEF}$ に直線 $\mathrm{BC}$ が刺さっていると考えます。
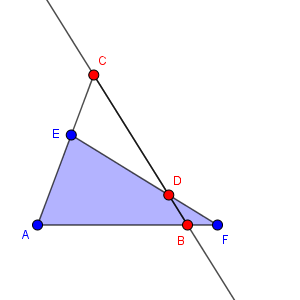
今度は、頂点、交点、と順番にたどっていくと、\[ \mathrm{A,B,F,D,E,C,A} \]となります。これを踏まえると、メネラウスの定理を使えば、
\begin{eqnarray}
\frac{\mathrm{AB}}{\mathrm{BF}} \cdot \frac{\mathrm{FD}}{\mathrm{DE}} \cdot \frac{\mathrm{EC}}{\mathrm{CA}} &=& 1 \\[5pt]
\frac{5}{1} \cdot \frac{\mathrm{FD}}{\mathrm{DE}} \cdot \frac{2}{5} &=& 1 \\[5pt]
\frac{\mathrm{FD}}{\mathrm{DE}} &=& \frac{1}{2} \\[5pt]
\end{eqnarray}となるので、 $\mathrm{FD:DE}=1:2$ と求められます。
おわりに
ここでは、メネラウスの定理について見てきました。例題でも見た通り、どの三角形とどの直線に対してメネラウスの定理を適用するかが、問題を解く上でポイントとなります。