【基本】チェバの定理
ここでは、チェバの定理とその証明について見ていきます。
チェバの定理
三角形の各頂点を通る直線について、以下で述べる、チェバの定理(Ceva's theorem) が成り立ちます。
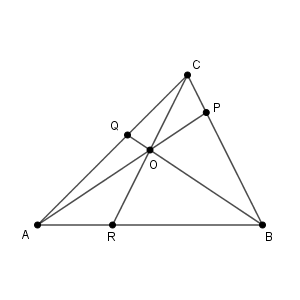
このとき、次の等式が成り立つ。\[ \frac{\mathrm{AR}}{\mathrm{RB}} \cdot \frac{\mathrm{BP}}{\mathrm{PC}} \cdot \frac{\mathrm{CQ}}{\mathrm{QA}}= 1 \]
大変そうな式ですが、次のように考えると見やすくなります(覚えやすくもなります)。まず、三角形の頂点と交点を分けます。そして、次のように、頂点・交点・頂点・交点… と順番にたどっていきます。
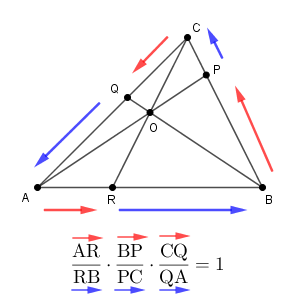
このようにたどりつつ、分子に「頂点→交点」、分母に「交点→頂点」を集めれば、\[ \frac{\mathrm{AR}}{\mathrm{RB}} \cdot \frac{\mathrm{BP}}{\mathrm{PC}} \cdot \frac{\mathrm{CQ}}{\mathrm{QA}}= 1 \]の式になります。
チェバの定理の証明
それでは、チェバの定理の証明をしていきます。

証明の方針は、辺の比を面積比に置き換える、というものです。直線 $\mathrm{AB}$ を底辺と考えると、 $\triangle\mathrm{ACR}$ と $\triangle \mathrm{BCR}$ の高さは等しいので、面積比は $\mathrm{AR:RB}$ となります。同様に、 $\triangle\mathrm{ARO}$ と $\triangle \mathrm{BRO}$ の面積比も $\mathrm{AR:RB}$ となります。このことから、
\begin{eqnarray}
\triangle \mathrm{ACO}
&=&
\triangle \mathrm{ACR} -\triangle \mathrm{ARO} \\[5pt]
&=&
\triangle \mathrm{BCR}\cdot\frac{\mathrm{AR}}{\mathrm{BR}} -\triangle \mathrm{BRO} \cdot\frac{\mathrm{AR}}{\mathrm{BR}} \\[5pt]
&=&
(\triangle \mathrm{BCR}-\triangle \mathrm{BRO}) \cdot\frac{\mathrm{AR}}{\mathrm{BR}} \\[5pt]
&=&
\triangle \mathrm{BCO}\cdot\frac{\mathrm{AR}}{\mathrm{BR}} \\[5pt]
\end{eqnarray}となるので、\[ \frac{\mathrm{AR}}{\mathrm{RB}} = \frac{\triangle \mathrm{ACO}}{\triangle \mathrm{BCO}} \]が成り立ちます。
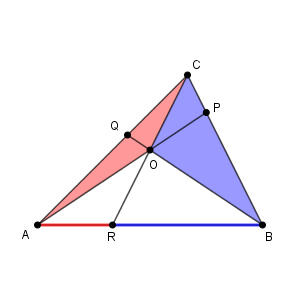
同様にすると、\[ \frac{\mathrm{BP}}{\mathrm{PC}} = \frac{\triangle \mathrm{ABO}}{\triangle \mathrm{ACO}},\ \frac{\mathrm{CQ}}{\mathrm{QA}} = \frac{\triangle \mathrm{BCO}}{\triangle \mathrm{ABO}} \]が成り立ちます。これらを使うと
\begin{eqnarray}
& &
\frac{\mathrm{AR}}{\mathrm{RB}} \cdot \frac{\mathrm{BP}}{\mathrm{PC}} \cdot \frac{\mathrm{CQ}}{\mathrm{QA}} \\[5pt]
&=&
\frac{\triangle \mathrm{ACO}}{\triangle \mathrm{BCO}} \cdot \frac{\triangle \mathrm{ABO}}{\triangle \mathrm{ACO}} \cdot \frac{\triangle \mathrm{BCO}}{\triangle \mathrm{ABO}} \\[5pt]
&=&
1
\end{eqnarray}となるので、チェバの定理が成り立つことがわかります。
チェバの定理の例題
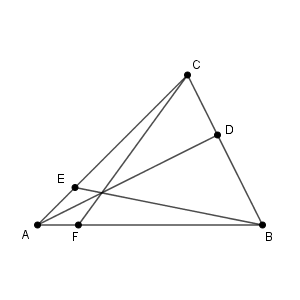
点の名前が違いますが、チェバの定理がそのまま使えます。チェバの定理より
\begin{eqnarray}
\frac{\mathrm{AF}}{\mathrm{FB}} \cdot \frac{\mathrm{BD}}{\mathrm{DC}} \cdot \frac{\mathrm{CE}}{\mathrm{EA}} &=& 1 \\[5pt]
\frac{\mathrm{AF}}{\mathrm{FB}} \cdot \frac{3}{2} \cdot \frac{3}{1} &=& 1 \\[5pt]
\frac{\mathrm{AF}}{\mathrm{FB}} &=& \frac{2}{9} \\[5pt]
\end{eqnarray}となるので、 $\mathrm{AF:FC}=2:9$ と求められます。
あっさり求められます。すごい威力ですね。
おわりに
ここでは、チェバの定理について見てきました。他に似た定理として、メネラウスの定理があります(参考:【基本】メネラウスの定理)。応用問題では、チェバとメネラウスのどちらを使うか、どの三角形に対して使うか、などを考える力が必要となってきます。





