【基本】標準正規分布

🕒 2023/05/14 🔄 2023/06/27

ここでは、標準正規分布について見ていきます。

📘 目次

標準正規分布

【基本】連続型確率分布では、連続的な値をとる確率変数について見ました。このような場合、確率密度関数の積分（面積）によって、確率を表す方法があることを見ました。

こうした連続型確率分布の中で、最も重要なものに、標準正規分布(standard normal distribution) があります。標準正規分布の次のような分布曲線になります。

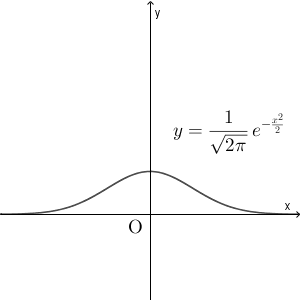
きれいな山の形をしています。この山は、 $y$ 軸について左右対称です。曲線の両側は $x$ 軸に近いところで、$x$ 軸と接することなく、ずっと伸びています。

密度関数は\[ f(x)=\dfrac{1}{\sqrt{2\pi}} e^{-\frac{x^2}{2}} \]になります。が、ちょっとこの式は何なんだという感じがしますね。これは指導要領が悪いのですが、ここに出てくる $e$ というものは、数学IIIで登場するものです。なので、ここで初登場するのはイマイチで、定義を述べるのも少し大変なんです。

なので、今の時点では、この $e$ は深追いしなくてもいいです。 $f(x)$ を全体で積分したときに結果が $1$ になる（全体の確率が $1$ になる）ように調整した数、つまり、\[ \int_{-\infty}^{\infty} \dfrac{1}{\sqrt{2\pi}} \blacksquare^{-\frac{x^2}{2}} dx=1 \]が成り立つように、黒い箱に入れる数を求めると $e$ という値だった、と考えてもらえばいいです。具体的には、 $e=2.71828\cdots$ という数で、無理数であることが知られています。

$e$ の指数には $-\dfrac{x^2}{2}$ があるので、グラフは $y$ 軸について対称になることがわかります。 $x=0$ のときに最大であることもわかります。

ちなみに、数学IIIを学ぶ人は、【基本】微分と関数のグラフを見ると、グラフのかきかたがわかるはずです。

正規分布表

$e$ を深追いしないことはいいとしても、では確率はどうやって求めるんだ、という話になりますよね。よくわからないものが入ったまま積分を計算することはできないので。

標準正規分布の確率を計算するときには、正規分布表(standard normal table) というものを使うのが一般的です。

正規分布表は、教科書の最後の方のページに載っているはずです。また、試験などで出題される場合は、正規分布表、もしくは、ピンポイントで必要な値が提供されるはずです。

次の表は、正規分布表を一部分だけ抜き出したものです。

$z_0$	$0.00$	$0.01$	$0.02$	…
$0.0$
$0.1$
$0.2$
$0.3$			$0.1255$
…

左側には、縦に $0.0$ から $3.0$ くらいが並んでいて、上側には、横に $0.00$ から $0.09$ が並んでいる、というのが典型的な表です。縦が、小数点第1位までを表していて、横が小数点第2位を表しています。つまり、上の表内の数字のある部分は、縦が $0.3$ で横が $0.02$ だから、 $z_0=0.32$ のときを表している、ということです。

$Z$ が標準正規分布に従うとすると、正規分布表は $P(0\leqq Z \leqq z_0)$ を表していることになります。小数点第4位あたりまでの値が載っています。

今考えている例では、 $P(0\leqq Z\leqq 0.32)=0.1255$ ということであり、正規分布表は、下の図の色のついた部分の面積が $0.1255$ であることを表しています。

このように、正規分布表を使えば、積分の計算をしなくても、確率の概算値がわかります。

普通は、正規分布表には $P(0\leqq Z\leqq z_0)$ の値がまとめられていて、共通テストで出題される場合もそうなっています。が、他の大学入試の問題や教科書によっては、別の書き方になっているケースもあります（例えば、$P(-\infty\leqq Z\leqq z_0)$ など）。定義をよく見て対応するようにしましょう。

正規分布表に関する疑問

正規分布表を見ると、いくつか疑問を抱く人がいるかもしれません。

まず、そもそも $z_0$ が負の場合はないのだろうか、ということですね。 $z_0$ が負の場合ももちろんありえるのですが、正規分布表には載っていません。ではどうするかというと、分布曲線が左右対称であることを利用します。

つまり、 $P(0\leqq Z\leqq z_0)=P(-z_0\leqq Z\leqq 0)$ であることを利用して、負の場合に対応することになります。

$0$ が基準じゃない場合はどうするんだろう、と思う人もいるかもしれません。例えば、 $P(1\leqq Z \leqq 2)$ のようなケースですね。この場合は、 $0$ 基準にしてから考えます。つまり、\[ P(0\leqq Z\leqq 2)-P(0\leqq Z\leqq 1) \]として、それぞれの値を正規分布表から読み取って計算します。 $Z=1$ の部分が気になる人がいるかもしれませんが、 $P(Z=1)$ は $0$ （面積が $0$ だから）なので気にしなくてもかまいません。

正規分布表の縦が $3.0$ くらいで終わっているのがなぜか、という疑問もあるでしょう。本来、縦はどこまでも伸びるはずです。しかし、よく考えてみると、全体の確率が $1$ で分布曲線が左右対称だから、 $P(0\leqq Z)$ は $0.5$ です。 $P(0\leqq Z \leqq 3.09)=0.4990$ と、ほとんど $0.5$ に近いので、これ以上見てもあまり意味がない、ということで、普通はこのあたりで掲載をやめています。