【標準】正規分布

ここでは、正規分布表を用いて、正規分布に関する確率を求める問題を見ていきます。

例題１

確率変数 $X$ が正規分布に従うときに、 $X$ の確率を正規分布表を用いて求める場合は、まずは、標準化を行う必要があります（参考：【基本】正規分布）。

標準化を行うには、平均（期待値）を引いて、標準偏差で割ればいいです。そのため、\[ Z=\frac{X-50}{9} \]とすると、 $Z$ は標準正規分布に従うようになります。

(1)で求めたい確率も、 $Z$ に関する式に変形していきます。
\begin{eqnarray} & & 50\leqq X\leqq 59 \\[5pt] & & 0\leqq X-50\leqq 9 \\[5pt] & & 0\leqq \frac{X-50}{9}\leqq 1 \\[5pt] \end{eqnarray}なので、\[ P(50\leqq X\leqq 59)=P(0\leqq Z\leqq 1) \]となります。右辺は、正規分布表の $1.00$ のところをみれば、わかります（参考：【基本】標準正規分布）。なので\[ 0.341 \]が答えとなることがわかります。

例題２

残りの問題も考えます。

先ほどと同じように、\[ Z=\frac{X-50}{9} \]として、標準正規分布が出てくるように変形します。

(2)は、次のように変形します。
\begin{eqnarray} & & X\geqq 63.5 \\[5pt] & & X-50\geqq 13.5 \\[5pt] & & \frac{X-50}{9}\geqq 1.5 \\[5pt] \end{eqnarray}このことから、 $P(Z\geqq 1.5)$ を答えればいいです。

ただ、正規分布表に載っているものは、 $P(0\leqq Z\leqq z_0)$ の確率なので、そのまま $1.50$ のところを見ても、答えはわかりません。ではどうするかというと、標準正規分布が $y$ 軸について左右対称であることを使います。これより、 $P(0\leqq Z)=0.5$ となることがわかります。

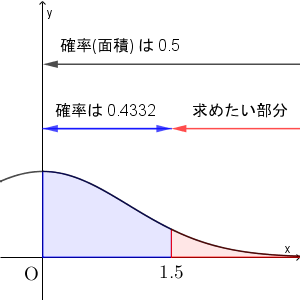
こうして、
\begin{eqnarray} P(X\geqq 63.5) &=& P(Z\geqq 1.5) \\[5pt] &=& P(0\leqq Z)-P(0\leqq Z\leqq 1.5) \\[5pt] &=& 0.5-0.4332=0.0668 \end{eqnarray}なので、 $0.067$ が答えとなります。

例題３

最後の問題も考えます。

(3)もまずは標準正規分布で表します。

\begin{eqnarray} & & 45.5 \leqq X\leqq 63.5 \\[5pt] & & -4.5 \leqq X-50\leqq 13.5 \\[5pt] & & -0.5 \leqq \frac{X-50}{9}\leqq 1.5 \\[5pt] \end{eqnarray}このことから、 $P(-0.5 \leqq Z\leqq 1.5)$ を答えればいいです。

ただ、正規分布表に載っているものは、 $P(0\leqq Z\leqq z_0)$ の確率なので、(2)と同様、正規分布表を見て終わり、というわけにはいきません。これはまずは以下のように分解します。
\begin{eqnarray} & & P(-0.5 \leqq Z\leqq 1.5) \\[5pt] &=& P(-0.5 \leqq Z\leqq 0)+P(0 \leqq Z\leqq 1.5) \end{eqnarray}こうすると、後半はすぐにわかります。前半は、正規分布表にマイナスの値が載っていませんが、正規分布が $y$ 軸について左右対称であることを使います。これにより \begin{eqnarray} & & P(-0.5 \leqq Z\leqq 0)+P(0 \leqq Z\leqq 1.5) \\[5pt] &=& P(0 \leqq Z\leqq 0.5)+P(0 \leqq Z\leqq 1.5) \\[5pt] &=& 0.1915+0.4332=0.6247 \end{eqnarray}となるので、 $0.625$ が答えとなります。

おわりに

ここでは、正規分布表を用いて、正規分布に関する確率を求める問題を見ました。まずは標準正規分布が出てくるように変形し、正規分布表を使って、求めたい確率（面積）を求められるようにしましょう。