【基本】連続型確率分布

🕒 2023/05/14 🔄 2023/06/03

ここでは、連続型確率分布の紹介をします。

📘 目次

連続型確率変数

【基本】二項分布では、 $n$ 回の試行で事象 $A$ が $X$ 回起こる、という状況を考えました。このように、 $X$ が回数を表す場合には、 $X$ は $0$ 以上の整数の値しかとりません。

しかし、状況によっては、 $X$ が（整数以外の）実数の値をとる状況を考えたいこともあります。例えば、 $n$ 人から1人を選んだときのその人の身長を $X$ cm とするとか、 $n$ 個の製品から1つ選んだときのその製品の耐久性を $X$ とする、などの場合です。

このような連続的な値をとる確率変数を、連続型確率変数(continuous probability distribution) といいます。連続確率変数ということもあります。一方、今まで扱っていたような、とびとびの値をとる確率変数のことを、離散型確率変数(discrete probability distribution) といいます。

以下では、連続型確率変数について考えていきます。

確率密度関数

ある、1万人の集団の身長のデータがあったとしましょう。相対度数分布表が以下のようになっていたとします（数字は適当に作りました）。

階級(cm) 以上～未満	度数	相対度数
167～168	9	0.0009
168～169	129	0.0129
169～170	1238	0.1238
170～171	3569	0.3569
171～172	3627	0.3627
172～173	1256	0.1256
173～174	165	0.0165
174～175	7	0.0007
計	10000	1

この中から1人を選んだとき、その人の身長を $X$ とします。すると、 $X$ が 170以上171未満（階級値 170.5）である確率は、上の表の相対度数である 0.3569 だと考えられます。つまり、 $X$ を階級値の値をとる確率変数と考えれば、この確率分布と相対度数の分布が一致することになります。

この確率分布を図示するには、次のようなヒストグラムをかけばいいです。

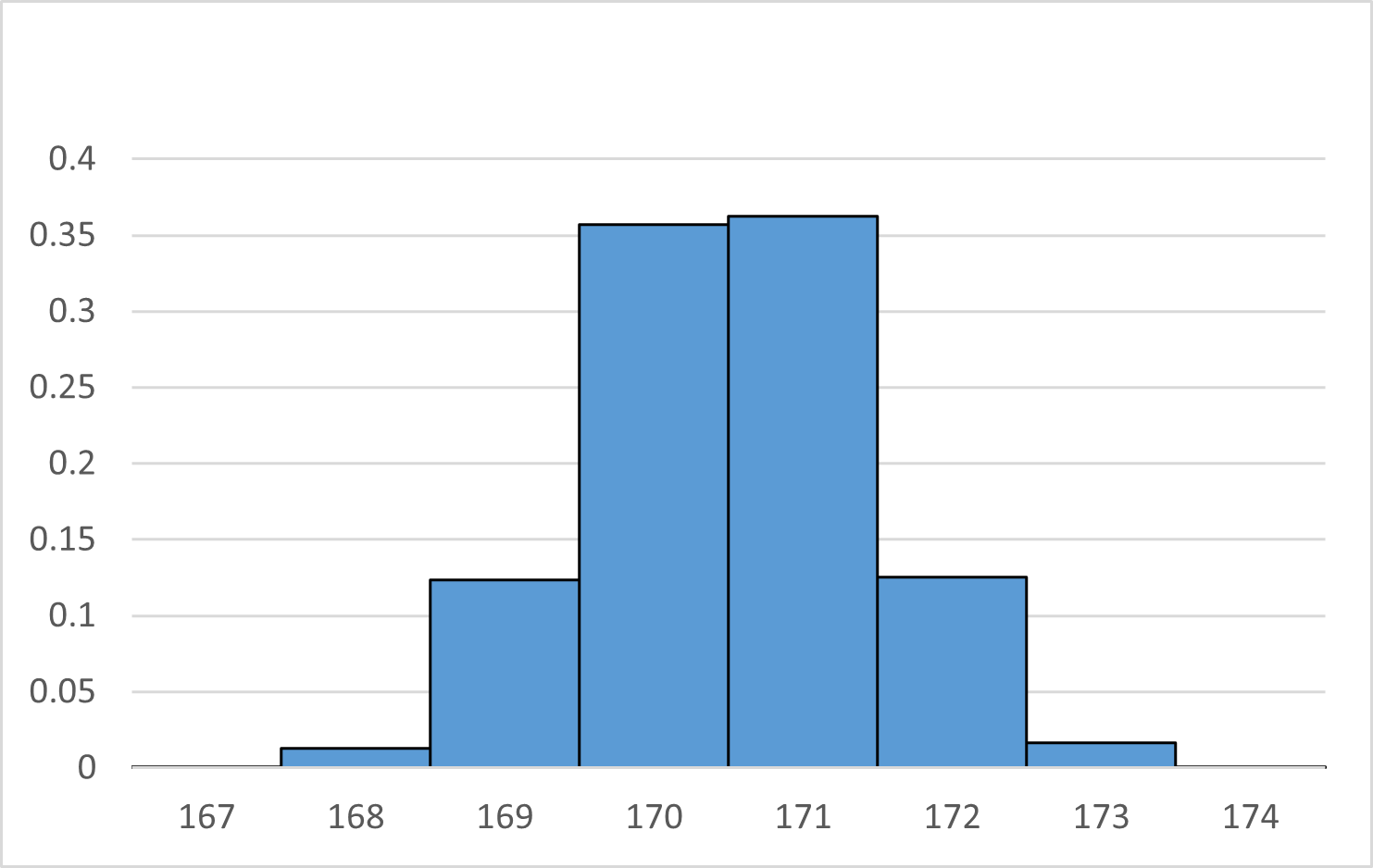
例えば、170のところにある長方形は、170cm以上 171cm未満の相対度数を表しています。

このようなヒストグラムをかけば、確率は、長方形の面積で表せる、と考えられます。例えば、 $P(170\leqq X\lt 172)$ は、中央にある2つの長方形の面積の和に対応します。

この階級の幅を狭めてみます。1cm を 0.5cm に狭めたところ、次のようになったとします。

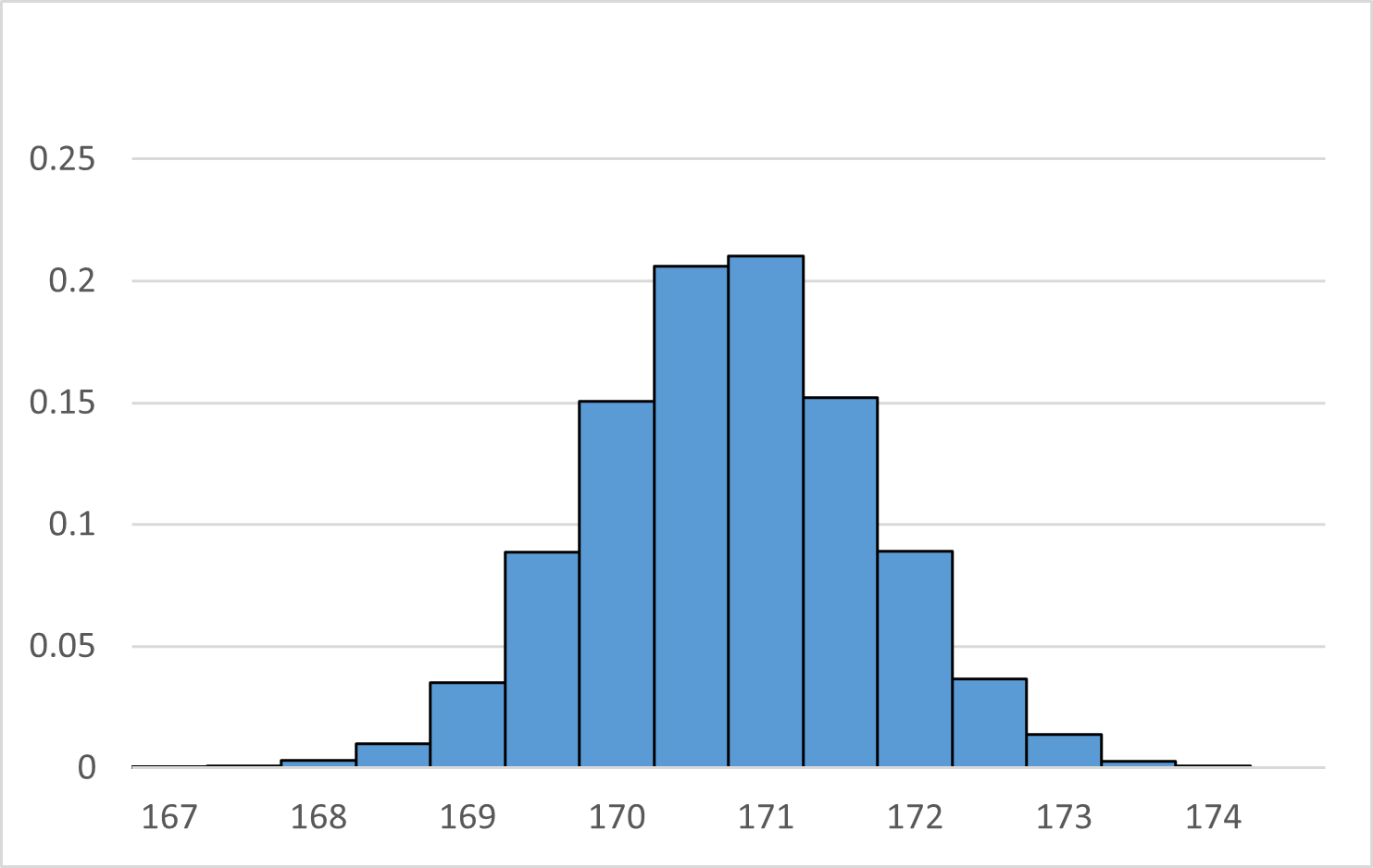
棒の幅が狭くなり、少し山の形が滑らかになりました。この場合でも、 $P(170\leqq X\lt 172)$ は、中央にある4つの長い棒の面積の合計になっています。（横の長さを $1$、縦の長さを確率と計算しています）

さらに階級の幅を半分にしてみます。

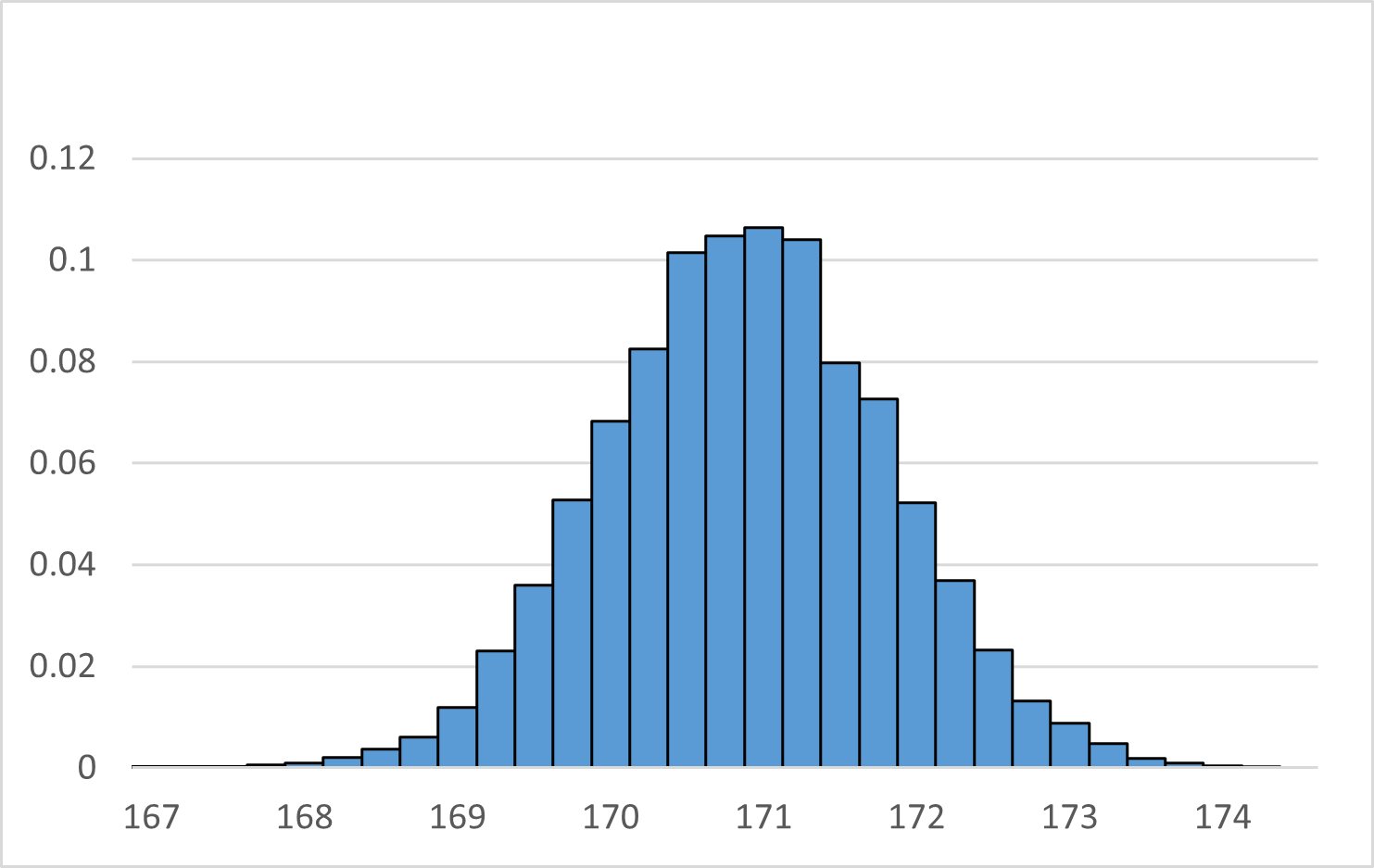
山の形がさらに滑らかになりました。このように幅を狭めていくと、ある曲線に近づいているように感じられます。

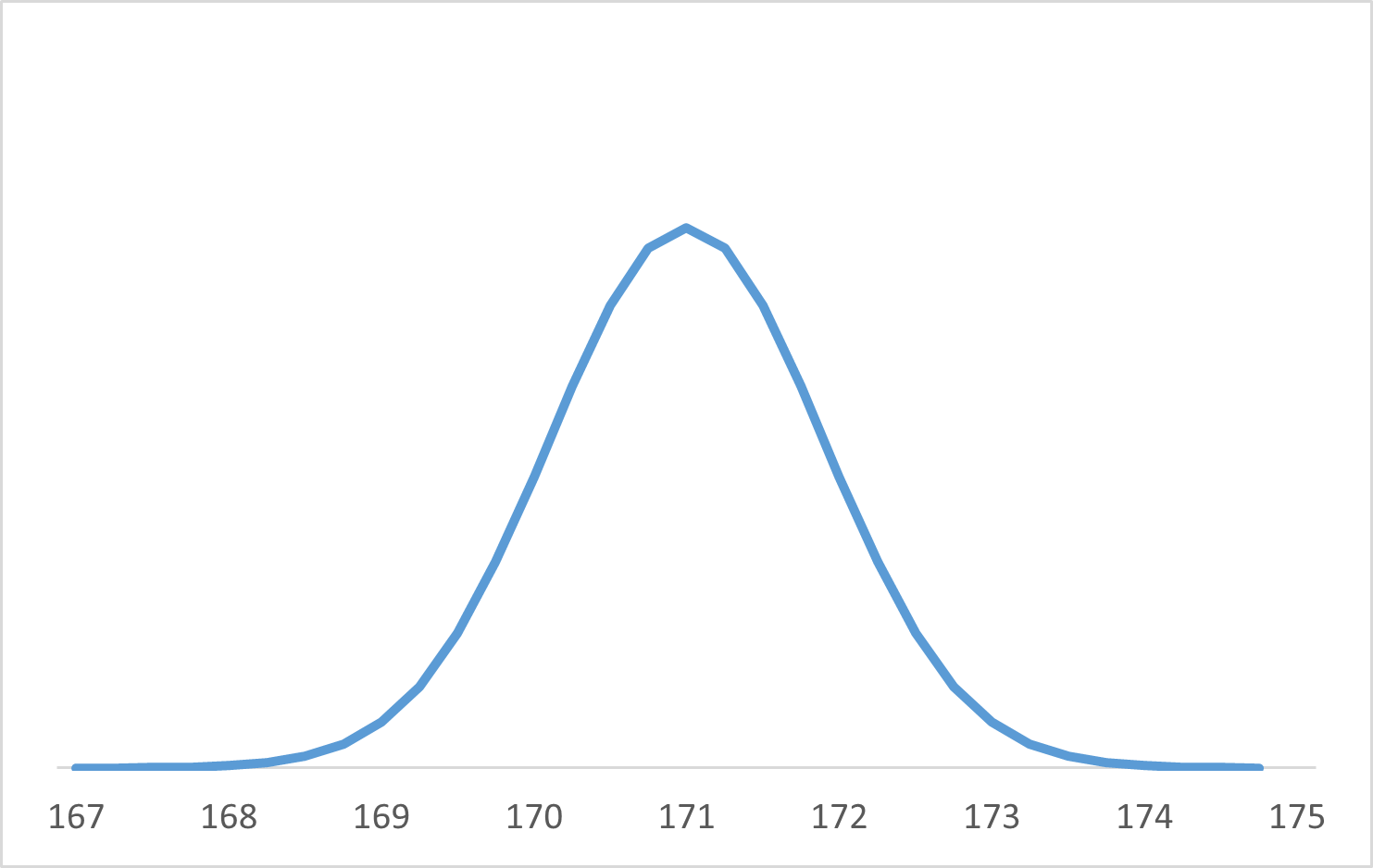
この曲線のことを、分布曲線(distribution curve) といいます。これは、各長方形の上側の辺の中点を結んだ折れ線の最終形と考えられます。

また、この場合でも、確率は、面積に対応しています。例えば、 $P(170\leqq X\lt 172)$ は、次の部分の面積となります。

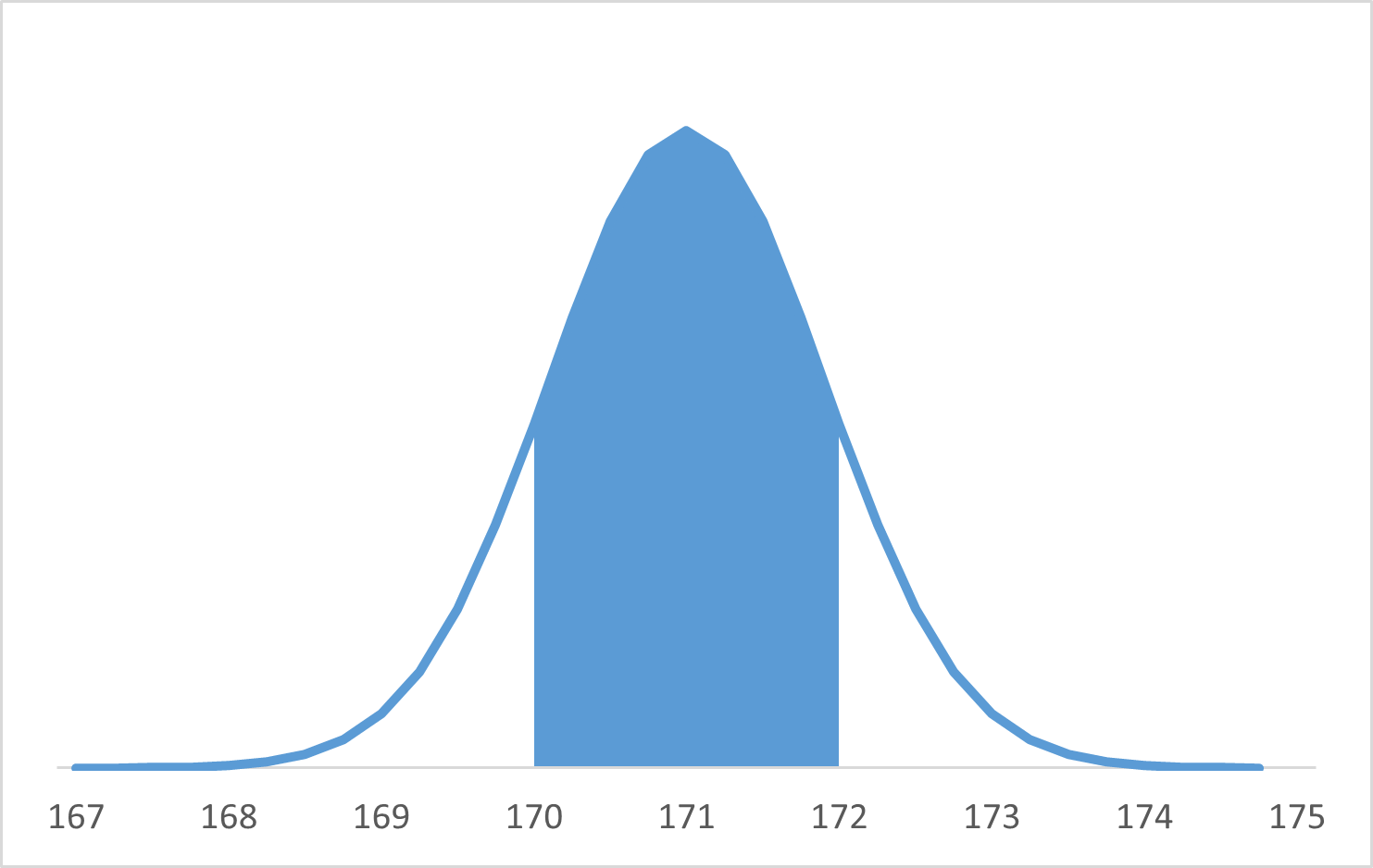
一般的に、連続な値をとる確率変数 $X$ の確率分布（連続型確率分布といいます）を表すときには、ある1つの曲線 $y=f(x)$ を対応させて、次のように、 $P(a\leqq X\leqq b)$ が面積と一致するように表す手法があります。

このとき、この関数 $f(x)$ を $X$ の確率密度関数(probability density function) といいます。（細かいですが、$X=b$ という1点だけの場合、確率は $0$ なので、 $P(X=b)=0$ となります。）

確率密度関数 $f(x)$ は、次の性質をもちます。記号や式の説明はすぐ後でします。

$f(x)\geqq 0$
$\displaystyle P(a\leqq X\leqq b)=\int_a^b f(x)dx$
$\displaystyle \int_{-\infty}^{\infty} f(x)dx=1$

まず、1つ目の $f(x)\geqq 0$ とは、 $y=f(x)$ のグラフをかいたときに、グラフ上の点は $x$ 軸上かその上側にある、ということです。これは、確率が 0以上であることに対応しています。

2つ目の $\displaystyle \int$ は、積分のことです。積分は、数学IIで習う内容です（参考：【基本】定積分）。

$\displaystyle \int_a^b f(x)dx$ とは、 $x$ 軸、 $x=a$, $x=b$ と $y=f(x)$ とで囲まれた部分の面積を表します。確率密度関数の積分（面積）を使って確率を表すことができる、という意味の式です。

3つ目の $\infty$ は無限大のことで、 $-\infty$ から $\infty$ までの積分とは、要するに、 $X$ のすべてのとり得る値をカバーするということです。すべてのケースを網羅した確率は $1$ だ、ということを表しています。

$X$ が $a$ 以上 $b$ 以下の値しかとらないことがわかっている場合は、3つ目の式は\[ \int_a^b f(x)dx=1 \]と表すこともできます。

抽象的な話が続いていますが、ここで、1つ例を挙げます。もっとも単純な連続型確率分布は、分布関数が次のようなケースです。

$0\leqq x\leqq 1$ で $f(x)=1$ となり、他では $f(x)=0$ となる場合です。この場合、 $a\leqq b$ なら、 $P(a\leqq X\leqq b)$ は $b-a$ となります。全体の確率は、 $1$ になっています。こういう場合も、連続型確率分布です。

連続型確率変数の期待値と分散

連続型確率変数の場合にも、期待値と分散があります。これらは、離散型確率変数の場合と比べながら見ると、わかりやすいでしょう。

まずは期待値についてです。 $X$ のとる範囲が限られていて、 $a\leqq x\leqq b$ であるとします。また、確率密度関数を $f(x)$ とします。
\begin{eqnarray} E(X) &=& \int_a^b x f(x) dx \\[5pt] E(X) &=& \sum_{k=1}^n x_k p_k \end{eqnarray}1行目が連続型、2行目が離散型です。どちらも $x$ に確率を掛けて足し合わせる、というイメージになっています。

次は分散です。期待値を $m$ とおきます。
\begin{eqnarray} V(X) &=& \int_a^b (x-m)^2f(x) dx \\[5pt] V(X) &=& \sum_{k=1}^n (x_k-m)^2 p_k \end{eqnarray}1行目が連続型、2行目が離散型です。こちらも、両方、 $x$ と期待値との差の2乗に確率を掛けて足し合わせる、というイメージになっています。

また、【基本】確率変数の分散の公式で見たように、離散型確率変数では\[ V(X)=E(X^2)-\{E(X)\}^2 \]が成り立ちましたが、これは連続型確率変数でも成り立ちます。 $X$ のとり得る値が $a\leqq X \leqq b$ のときに示してみます。
\begin{eqnarray} & & V(X) \\[5pt] &=& \int_a^b (x-m)^2 f(x)dx \\[5pt] &=& \int_a^b (x^2-2mx+m^2) f(x)dx \\[5pt] &=& \int_a^b x^2 f(x)dx -2m\int_a^b x f(x)dx +m^2\int_a^b f(x)dx \\[5pt] &=& \int_a^b x^2 f(x)dx -m^2 \end{eqnarray}ここで、下から2行目から最後の式への変形は、 $xf(x)$ の積分が $m$ であること、 $f(x)$ の積分が $1$ であることを使っています。

数学IIの範囲では、積分できる関数が少ないため、これらの式を使って計算する機会はほとんどないでしょう。数学IIIでも積分を学びますが、数学IIIも学ぶ人は、連続型の期待値や分散を計算する問題に出くわすかもしれません。