【標準】二項分布と正規分布

🕒 2023/05/22

ここでは、$n$ が十分大きい場合に、二項分布を正規分布で近似する問題を見ていきます。

📘 目次

例題１

例題

当たり2本を含む5本のくじから、2本を引く試行を考える。この試行を1600回繰り返したとき、2本とも当たりを引いた回数が $130$ 以上 $175$ 以下となる確率を、四捨五入によって小数点第2位まで求めなさい。正規分布による近似、正規分布表を用いてもよい。

2本とも当たりを引く回数を $X$ とすると、 $X$ は二項分布に従います。そこで、まずはどんな二項分布なのかを考えます。

はじめに、2本とも当たりを引く確率を考えます。全部で5本、当たりは2本で、2本を引くのだから
\begin{eqnarray} \frac{ {}_2 \mathrm{C}_2 }{ {}_5 \mathrm{C}_2 } &=& \frac{1}{10} \\[5pt] \end{eqnarray}となります。

こうして、 $X$ は二項分布 $B(1600, \frac{1}{10})$ に従うことがわかります。

次に、期待値は、$np$ で求められるので、\[ E(X)=1600\cdot\frac{1}{10}=160 \]となります。分散は $np(1-p)$ で求められるので、\[ V(X)=1600\cdot\frac{1}{10}\cdot\frac{9}{10}=144 \]となります。標準偏差は $\sqrt{144}=12$ となります。

ここで、二項分布が正規分布で近似できることを使うと、 $X$ は近似的に、正規分布 $N(160, 12^2)$ に従うことがわかります。

さらに、$\dfrac{X-160}{12}$ は近似的に、標準正規分布に従います。また、
\begin{eqnarray} & & 130 \leqq X \leqq 175 \\[5pt] & & -30 \leqq X-160 \leqq 15 \\[5pt] & & -2.5 \leqq \frac{X-160}{12} \leqq 1.25 \\[5pt] \end{eqnarray}となることから、 $Z$ を標準正規分布に従う確率変数とすると、\[ P(-2.5\leqq Z\leqq 1.25) \]を答えればいいことになります。

正規分布

ここまでで、代表的な離散型確率変数である二項分布と、代表的な連続型確率変数である正規分布についてみてきました。これらは全然違うように見えますが、実は関係があります。

サイコロを $n$ 回投げて、1の目が $X$ 回出るとします。 $X$ の分布は $B\left(n,\frac{1}{6}\right)$ に従います。ヒストグラムをかくとこのようになります。

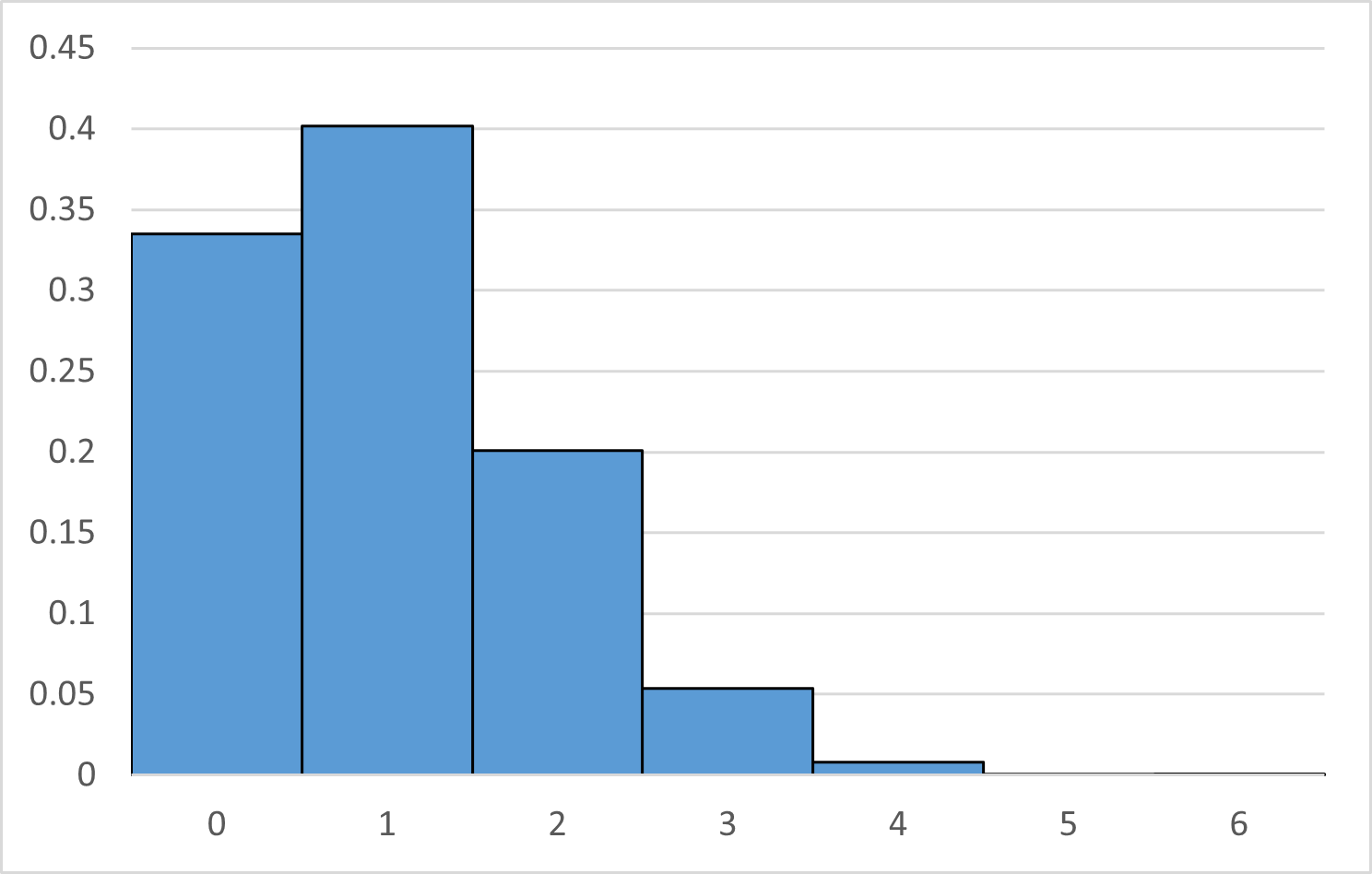
これは、 $n=6$ の場合です。期待値が $1$ なので、 $1$ 付近の確率が高くなっており、徐々に確率は下がっています。さらに回数を増やして $n=60$ にすると、次のようになります。

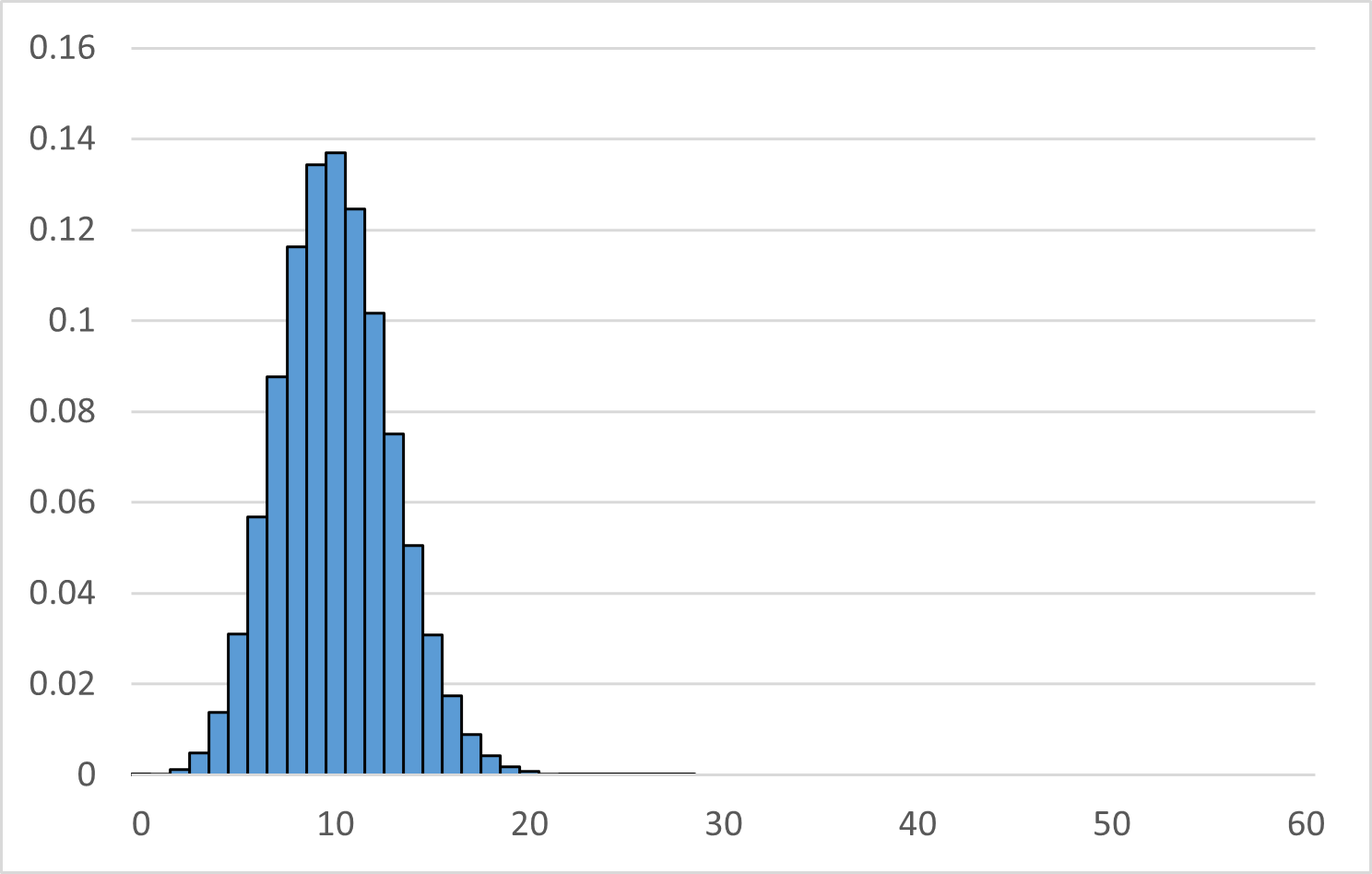
先ほどよりも、山の形がハッキリしてきました。さらに増やすとこのようになります。 $n=600$ とします。（見にくいので、棒を囲む黒線は非表示にしています。）

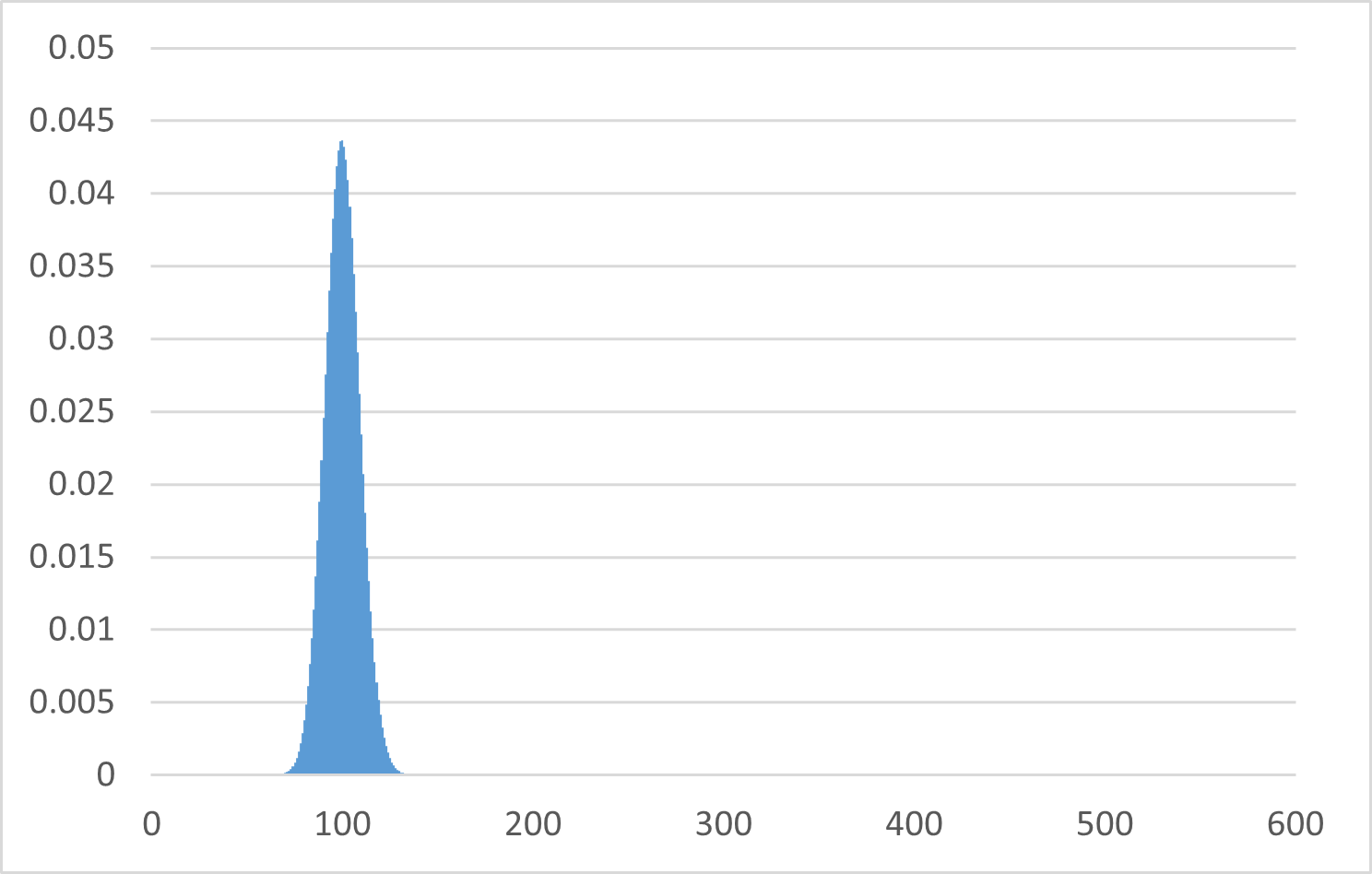
$X$ は $0$ から $600$ までの値を取りうるので、上のような区間をとっていますが、端のほうの確率はほとんど見えませんね。 $X=100$ あたりの部分を拡大して表示すると、次のようになります。

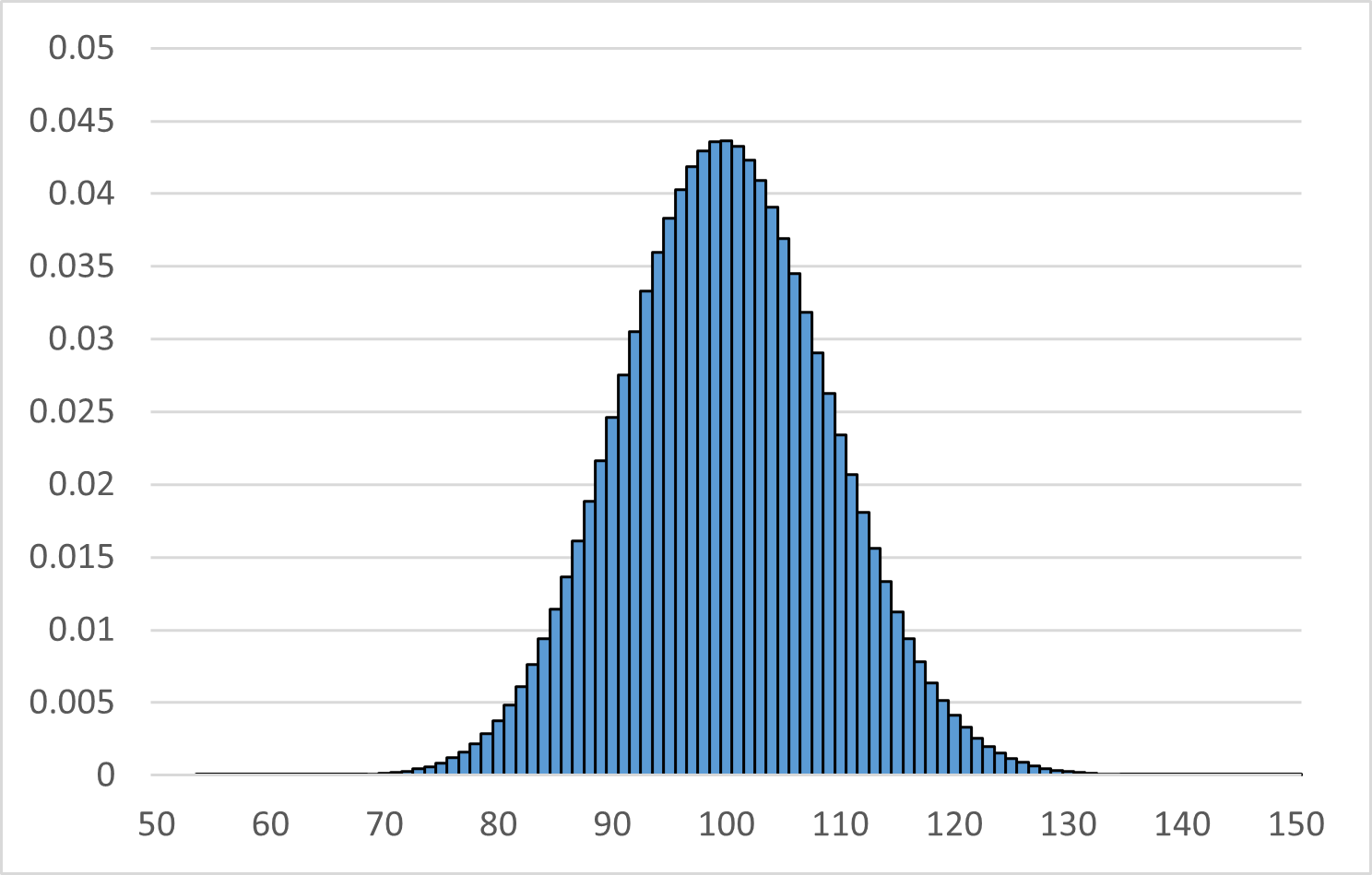
これと、正規分布 $N\left(100,\frac{250}{3}\right)$ の分布曲線とを比較してみます。この $100$ と $\frac{250}{3}$ は、二項分布の期待値 $600\cdot\dfrac{1}{6}=100$ と分散 $600\cdot\dfrac{1}{6}\cdot\dfrac{5}{6}=\dfrac{250}{3}$ に由来しています。

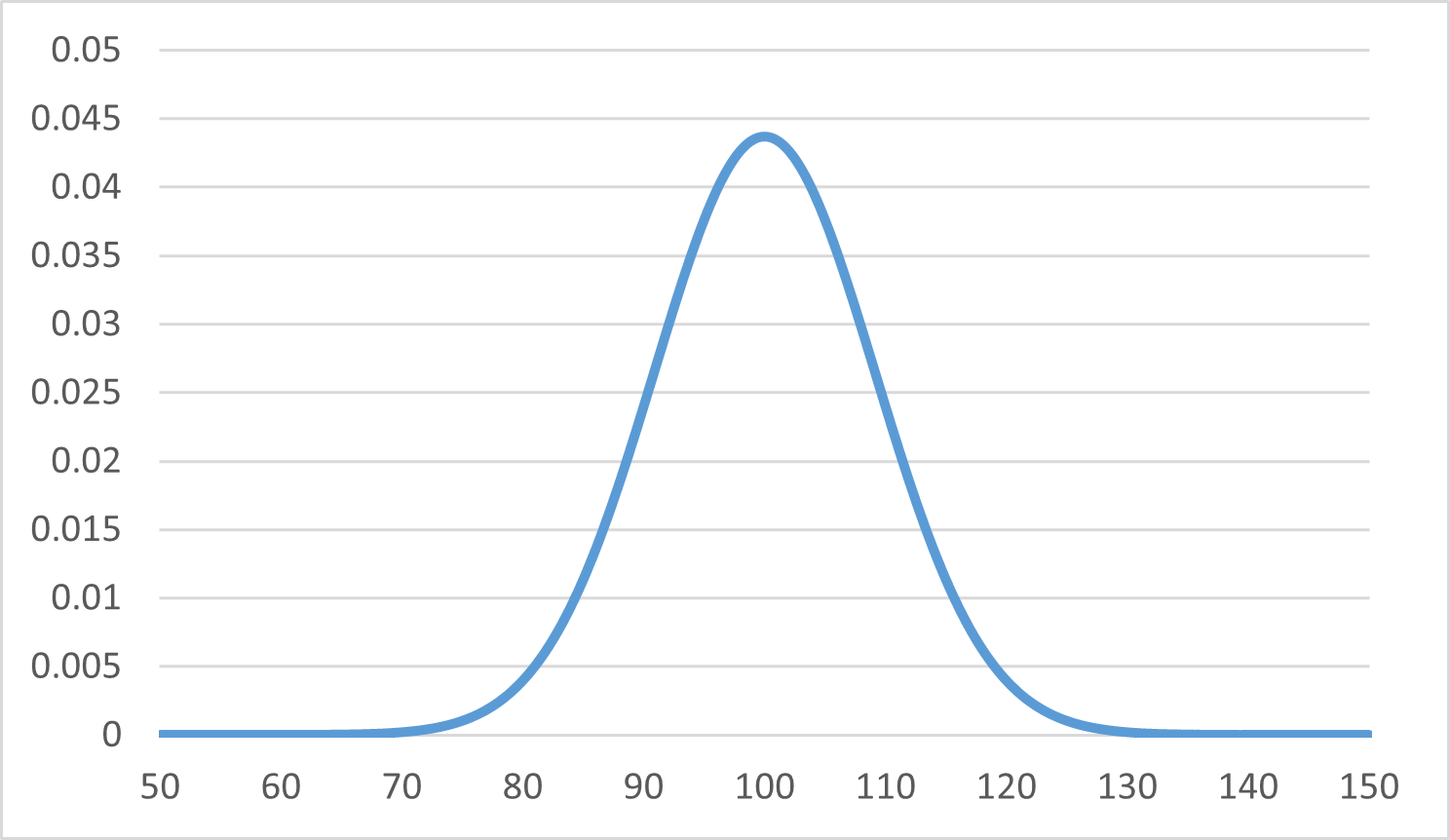
すごく形が似ていますね。実際に確率を比較してみましょう。 $100$ 以上 $100+\frac{250}{3}=\frac{550}{3}$ 以下となる確率は、それぞれ次のようになります。 $X$ が二項分布、 $Y$ が正規分布に従っているとします。なお、二項分布の方は、コンピュータを使って求めています。
\begin{eqnarray} P\left(100\leqq X \leqq \frac{550}{3}\right) &=& 0.3678\cdots \\[5pt] P\left(100\leqq Y \leqq \frac{550}{3}\right) &=& 0.3413\cdots \\[5pt] \end{eqnarray} 近い値になっています。さらに $n$ を増やして $n=6000$ とすると、上の確率の差（ $m\leqq X\leqq m+\sigma$ の確率）は、さらに縮まって、$0.002$ 程度となります。

ここでは具体的な例を見ましたが、これは一般的に成り立ちます。 $n$ が十分大きい場合には、二項分布 $B(n,p)$ は、正規分布 $N(np, np(1-p))$ で近似することができます。残念ながら、高校の範囲でこれを示すことは難しいのですが、試験などではこの内容を使ってもかまいません。

「十分大きい」とは具体的にどれくらいなのか気になるかもしれませんが、問題を解く場合には、「十分大きいので近似できるものとする」というような文言が書かれているはずです。過去の共通テストの問題を見てみると、 $n$ が数百くらいであれば、「近似できる」と書かれています。実務上では、計算にどれくらいの精度が必要かによって、必要な $n$ の大きさが変わってくるでしょう。

近似できると何がいいか

$n$ が大きい場合に二項分布を正規分布で近似できると、二項分布の確率が計算しやすくなります。

二項分布の場合、確率は以下の値を足し合わせて求める必要があります。\[ {}_n\mathrm{C}_k p^k(1-p)^{n-k} \]$n$ が大きくなると、一般的に ${}_n\mathrm{C}_k$ はすごく大きな値になり、 $p^k(1-p)^{n-k}$ はすごく小さな値となり、人間が手計算で求めるには限界があります。

ところが、正規分布が使えるなら、【基本】正規分布で見たように、標準正規分布に変換して、正規分布表を使って確率を求めることができるようになります。

先ほどの例であれば、二項分布で $P(100\leqq X\leqq \frac{550}{3})$ を計算するのは大変ですが、正規分布であれば
\begin{eqnarray} & & 100\leqq X\leqq \frac{550}{3} \\[5pt] & & 0\leqq X-100\leqq \frac{250}{3} \\[5pt] & & 0\leqq \frac{X-100}{\frac{250}{3}}\leqq 1 \\[5pt] \end{eqnarray}と変形でき、 $Z=\dfrac{X-100}{\frac{250}{3}}$ は標準正規分布に従うので、正規分布表から $P(0\leqq Z\leqq 1)=0.3413$ と求められます。

このように、離散的な問題を連続的な問題に近似・変形して考えることは、この例に限らず、実務上の場面でも行うことがあります。