【基本】正規分布

🕒 2023/05/16 🔄 2023/05/19

ここでは、正規分布について見ていきます。

📘 目次

正規分布

【基本】標準正規分布では、標準正規分布についてみましたが、名前からもわかる通り、これは「標準形」です。標準形の密度関数は次のような形でした。\[ \dfrac{1}{\sqrt{2\pi}} e^{-\frac{x^2}{2}} \]実は、一般的には、密度関数は次のような形をしています。\[ \dfrac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(x-m)^2}{2\sigma^2}} \]このような密度関数で表される確率分布を、正規分布(normal distribution) といいます。標準形の式もなかなか大変そうでしたが、一般形はさらにパワーアップしていますね。この式で新しく出てきた $m$ は期待値で、$\sigma$ は標準偏差を表しています。といっても、実際に計算して確かめることは、今の時点では難しいのですが。

期待値 $m$ 、標準偏差 $\sigma$ の正規分布は、 $N(m,\sigma^2)$ と表します。

正規分布の密度関数 $\dfrac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(x-m)^2}{2\sigma^2}}$ で、 $m=0, \sigma=1$ とすると、標準正規分布の密度関数になることがわかります。そのため、標準正規分布は、 $N(0,1)$ と表します。

期待値・標準偏差と分布曲線の関係

正規分布の分布曲線についてみていきます。

まず、正規分布と標準正規分布の密度関数を見比べてみます。
\begin{eqnarray} & & \dfrac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(x-m)^2}{2\sigma^2}} \\[5pt] & & \dfrac{1}{\sqrt{2\pi}} e^{-\frac{x^2}{2}} \end{eqnarray} 標準正規分布の $x^2$ の部分が、正規分布では $(x-m)^2$ になっていますね。二次関数のところでもみたように、 $y=(x-m)^2$ のグラフは $y=x^2$ のグラフを $x$ 軸方向に $m$ だけ移動したものになります。同様に、正規分布の分布曲線も、 $x$ 軸方向に $m$ だけ移動したものになります。標準正規分布の場合は、 $x=0$ のときに最大になりましたが、正規分布の場合は、 $x=m$ のときに最大になります。

$\sigma$ は散らばり具合を表していることからも想像できる通り、値が大きくなると、山が左右に広がっていきます。また、分布曲線と $x$ 軸との間の部分の面積は $1$ になることから、山が広がる分、高さは低くなります。

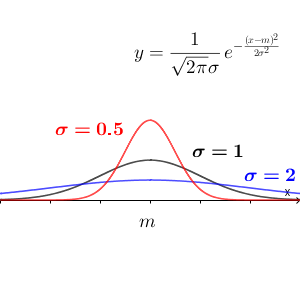
$\sigma$ が小さくなると、逆に、幅は狭くなり、高さは高くなります。

つまり、期待値 $m$ はどれだけ左右に移動するかを表していて、標準偏差 $\sigma$ はどれだけ左右に広がるか、どれだけ高さが低くなるかを表していることになります。

正規分布の標準化

確率変数 $X$ が正規分布 $N(m,\sigma^2)$ に従うとします。この場合、もちろん確率の計算をしたいのですが、実際には $\dfrac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(x-m)^2}{2\sigma^2}}$ の積分を計算することはできません。標準正規分布の場合は、正規分布表というのがありましたが、これは一般の正規分布の場合には使えません。

ではどうするかというと、 $X$ を標準化する、という手法を使います。

一般に、 $X$ から $a$ を引くと、期待値も $a$ だけ減ります。また、正の値 $a$ で割ると、標準偏差は $\dfrac{1}{a}$ 倍されます（参考：【標準】確率変数の標準化）。なので、 $Z=\dfrac{X-m}{\sigma}$ は、期待値が $0$ で標準偏差が $1$ となります。また、密度関数は $\dfrac{1}{\sqrt{2\pi}} e^{-\frac{x^2}{2}}$ となり、標準正規分布に従うことが知られています（これも現時点で示すのは難しいです）。

このように変換すれば、正規分布表を使って、確率を計算することができます。

例えば、確率変数 $X$ が、正規分布 $N(3,2^2)$ に従うとします。この場合に、 $P(3\leqq X\leqq 6.92)$ となる確率を考えてみます。 $X$ を $\dfrac{X-3}{2}$ にしたいので、
\begin{eqnarray} & & 3 \leqq X \leqq 6.92 \\[5pt] & & 0 \leqq X-3 \leqq 3.92 \\[5pt] & & 0 \leqq \frac{X-3}{2} \leqq 1.96 \\[5pt] \end{eqnarray}と変形します。これより、正規分布表の $1.96$ のところを見れば、 $0.4750$ であることがわかるので、\[ P(3\leqq X\leqq 6.92)=0.475 \]となることがわかります。

ざっくりとした確率

先ほど見たように、一般の正規分布の場合、確率を計算するには標準正規分布に変換します。ただ、この変換をせずに、ざっくりとした確率を把握することがあります。

$X$ が $N(m,\sigma^2)$ に従うとします。この場合、 $X$ が期待値 $m$ から $\sigma$ 以内の確率は、$68.3$ %程度となります。

上の図でいうと、色のついた部分の面積が $0.683$ 程度になる、ということです。これは、標準化すると、正規分布表の $1.00$ のところの確率 $0.3413$ の2倍で計算できます。

同様に、$X$ が期待値 $m$ から $2\sigma$ 以内の確率は、$95.4$ %程度となります。

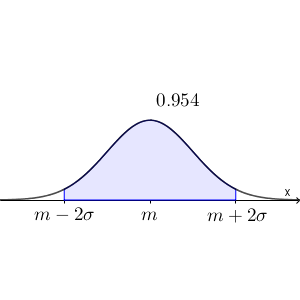
これも、標準化して正規分布表から確かめられます。正規分布表の $2.00$ のところの確率 $0.4772$ の2倍で計算できます。

$X$ が期待値 $m$ から $3\sigma$ 以内の確率は、$99.7$ %程度となります。

図で見ると、ほぼ全体をカバーしているように見えますね。

実務では、統計情報として、期待値・標準偏差が与えられることがあります。そういうときに、正規分布で近似できると考えられる場合は、「 $2\sigma$ 以内には、全体の約 95%が含まれている」などとざっくり考えることができて便利です。

例えば、大学入試の模試などでよく使われる指標に、偏差値があります。偏差値は、平均が $50$ で標準偏差が $10$ となるように変換されています。なので、点数の分布が正規分布に従うとすると、ある模試での偏差値が $70$ 以上だった場合、 $2\sigma$ 以上だから、全体の95.4%以外の部分の上半分にいることになり、だいたい上位2.3%以内にいる、とわかります。1万人が受けていたら、上位230位以内、ということです。