【基本】媒介変数表示

🕒 2018/05/25 🔄 2023/05/01

ここでは、媒介変数表示の基本的な事柄を見ていきます。

📘 目次

円の方程式と三角関数

単位円（原点を中心とした半径1の円）の方程式は、\[ x^2+y^2=1 \]と書くことができます（参考：【基本】円の方程式）。

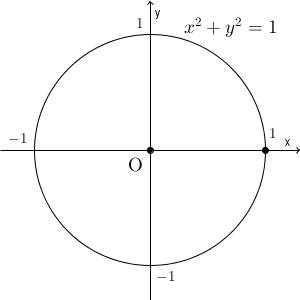
このように、今まで扱ってきた直線や、放物線、円といった曲線の方程式は、 $x,y$ の方程式で表してきました。

また、【基本】三角関数の定義で見たように、単位円は、三角関数の定義にも用いました。原点を中心として、点 $\mathrm{ A }(1,0)$ を反時計回りに $\theta$ だけ回転したとき、その点の x 座標を $\cos\theta$ とし、 y 座標を $\sin\theta$ とするのでしたね。

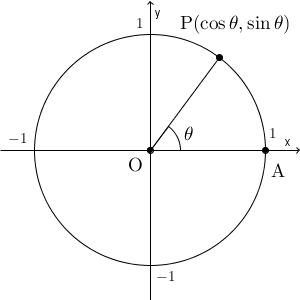
これは、「単位円から三角関数を定義する」というように利用していますが、この式を逆に利用して、「三角関数から単位円を表す」ということもできます。つまり、単位円の円周上の点を $\mathrm{ P }(x,y)$ としたとき、 $\angle \mathrm{ POA }=\theta$ とすれば
\begin{eqnarray} x &=& \cos\theta \\ y &=& \sin\theta \\ \end{eqnarray}と表すことができる、ということです。この式で $\theta$ を動かせば、単位円周上のすべての点を表すことができます。そのため、この表記も、単位円を表していると考えることができます。

媒介変数表示

単位円を表す方法が2種類出てきました。1つ目は\[ x^2+y^2=1 \]という形です。これはなじみのある、 $x,y$ だけを用いた方程式の形ですね。2つ目は
\begin{eqnarray} x &=& \cos\theta \\ y &=& \sin\theta \\ \end{eqnarray}という形です。1つ目と異なるのは、 $x,y$ の関係を表すために、別の文字 $\theta$ を用いている点です。

このように、曲線 C 上の点 $\mathrm{ P }(x,y)$ が、ある変数 $t$ を用いて\[ x=f(t),y=g(t) \]と表されるとき、このような表し方を C の媒介変数表示(parametric representation) といいます。媒介とは、「2つのものの間に入って仲立ちするもの」という意味があります。この場合は、 $x$ と $y$ の間に、別の変数 $t$ が入って、両者の関係を表している、ということですね。

この媒介変数表示で使われる変数のことを、媒介変数(parameter) といいます。

媒介変数を用いると、複雑な曲線もシンプルに表現できるようになる場合があります。当面は、よく知っている曲線を媒介変数を用いるとどのように書けるかを見ていきますが、今まで見たことのない曲線もいずれ扱うことになります。なぜ見たことのない曲線が出てくるかというと、今までのように、 $x,y$ だけを用いた方程式では表現できない曲線も、媒介変数を使えば表せるようになるからです。

ちなみに、媒介変数を使った表示の仕方は、1通りではありません。例えば、先ほどの単位円の例でいうと
\begin{eqnarray} x &=& -\cos\theta \\ y &=& -\sin\theta \\ \end{eqnarray}としても、やはり、これは単位円を表しています。 $\theta$ に対応する点は異なりますが、曲線全体は同じものになります。

また、媒介変数の取りうる値によっては、曲線のすべてではなく、一部のみを表すこともあります。例えば
\begin{eqnarray} x &=& \sqrt{t} \\ y &=& \sqrt{1-t^2} \end{eqnarray}とすると、 $t$ を動かせば、点 $(x,y)$ は単位円の上を動きます。しかし、 $\sqrt{t}\geqq 0$, $\sqrt{1-t^2}\geqq 0$ なので、この媒介変数表示は、単位円の全体ではなく、単位円の $x,y\geqq 0$ の部分だけを表すことになります。媒介変数の取りうる値の範囲は、注意して考える必要があります。