【基本】平均値の定理

ここでは、平均値の定理について見ていきます。平均値の定理は抽象的な内容なので、まずは具体的な利用例を見た後に、定理の内容を紹介することにします。

sin同士の差

この例題を考えてみましょう。

$0\lt x\lt \dfrac{\pi}{2}$ のときは $y=\sin x$ は単調増加なのだから、左側の不等号については問題ないでしょう。

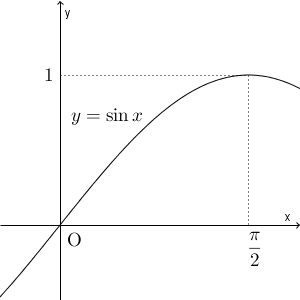
問題は右側の不等号です。不等式の中央にある分数は、分母が角度で分子が三角関数なので、この式を変形して考えていくのは少し難しそうです。そこで、方針を変えて、グラフを用いて考えてみることにしましょう。真ん中の分数は、 $(a,\sin a)$ と $(b,\sin b)$ とを結んだ直線の傾きなので、この2点と直線を上の図に追加してみましょう。この2点を、それぞれ点A と点B と呼ぶことにしましょう。

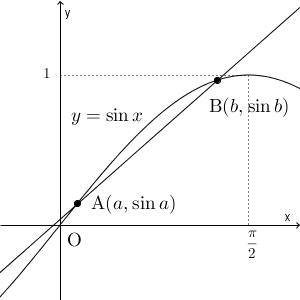
また、中央の分数は、 $b\to a$ とすれば、微分係数の定義が現れます。なので、接線の傾きと関係がありそうです。そこで、点A と点B での接線を追加してみましょう。

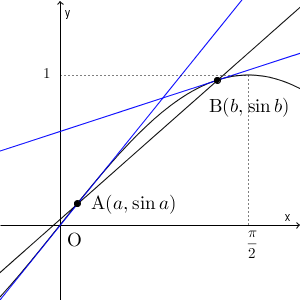
この図を用いて、直線AB の傾きと比較してみます。点A での接線の傾きは直線AB の傾きより大きく、点B での接線の傾きは直線AB の傾きより小さいことがわかります。さらに、 $x$ を動かしながら接線もあわせて動かしていくと、接線の傾きは、次のように連続的に変化していくことがわかります。

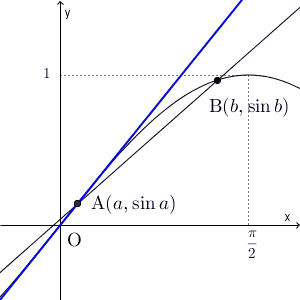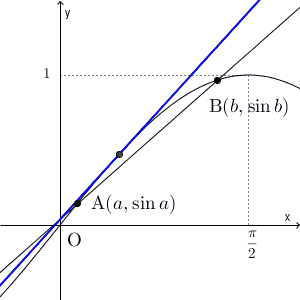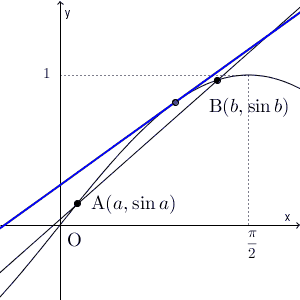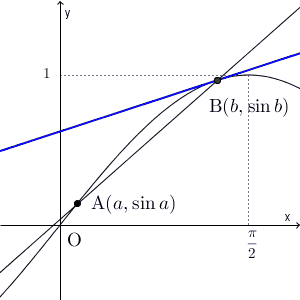
直線AB より大きい傾きから小さい傾きへと連続的に変化していくので、途中で直線AB と同じ傾きの接線が現れることがわかります。

A,B が別の場所にあっても、直線AB より大きい傾きから小さい傾きへと連続的に変化していくので、同じように、直線AB と同じ傾きの接線が途中で現れます。

上のように、同じ傾きの接線がひけるときの、接点の x 座標を $c$ とおきましょう。 $c$ は、 $a,b$ によって変わりますが、具体的にどのような値なのかは、求めずに話を進めていきましょう。

$y=\sin x$ を微分すると\[ y'=\cos x \]なので、接線の傾きは $\cos c$ です。これは直線AB の傾きでもあります。

$a\lt c\lt b$ であり、 $a,b$ の範囲から $ 0\lt c\lt \dfrac{\pi}{2}$ だから、\[ 0\lt \cos c\lt 1 \]であることがわかります。この $\cos c$ は、直線AB の傾きとも一致しているのだから、\[ 0\lt\frac{\sin b-\sin a}{b-a}\lt 1 \]となることがわかります。これで、示したかった不等式が示せました。

ポイントとなったのは、\[ \frac{\sin b-\sin a}{b-a} \]を直接考えることが難しいので、接線の傾きがこの値と同じになるような別の点を利用した、という箇所です。そのような接線・接点はどこか、具体的に求めなくても不等式が示せてしまう、というのは、少し不思議な感じがしますね。

平均値の定理

先ほどの例題で\[ \frac{\sin b-\sin a}{b-a} \]と同じ値の傾きとなる接線を利用しました。このような接線が存在することを、一般的な内容にしたものが、平均値の定理です。

この定理の意味を図形的に考えてみましょう。左辺にある分数は、 $(a,f(a))$ と $(b,f(b))$ とを結んだ直線の傾きです。右辺は接線の傾きなので、この間のどこかの点で、この直線と同じ傾きの接線がひける、ということです。

もし同じ傾きの接線が引けなければ、もとの直線よりもどんどん上に行ってしまうか、もとの直線よりもどんどん下に行ってしまいます。なので、どこの点かはわからないけれども、どこかの点では同じ傾きの接線がひけることが、直感的にわかると思います。そのような接線は1本だけとは限りませんが、少なくとも1本はある、ということをこの定理では言っています。

この平均値の定理の証明は難しいため、別の機会でとりあげることにします。高校の教科書では、詳しい証明が載っていなかったり、巻末に載っているだけであったりしますが、定理自体は試験で使ってもいい内容です。

おわりに

ここでは、平均値の定理を使った例と、平均値の定理の内容、その図形的な意味を見てきました。図を見て考えれば当たり前な気がするし、抽象的過ぎてこれをどう使って問題を解くのかよくわからないかもしれませんが、平均値の定理を使った問題は、【応用】平均値の定理と不等式 などで見ることにします。