【基本】無限等比級数

ここでは、項が無限個ある等比数列の和について見ていきます。

無限等比級数

【基本】無限級数で見た通り、項が無限個ある数列の和を無限級数といいました。この数列が等比数列の場合は、特に、無限等比級数(infinite geometric series) といいます。

無限等比級数の収束や発散について考えてみましょう。

初項が $1$ で、公比が $r$ の等比数列 $\{ r^{n-1} \}$ について考えてみます。このような等比数列の和は、【基本】等比数列の和で見た通り、 $r=1$ かそれ以外かで結果が異なります。

$r=1$ の場合は、すべての項が $1$ なので、 $n$ 項目までの和は $n$ となります。よって、 $n\to\infty$ としたときには、正の無限大に発散することになります。

$r\ne 1$ の場合は、 $n$ 項目までの和は\[ \frac{r^n-1}{r-1} \]となります。この部分和が収束するか発散するかは、結局 $r^n$ の部分がどうなるかによります。それは、次のように式変形をすれば、よりはっきりします。
\begin{eqnarray} \frac{r^n-1}{r-1} &=& \frac{r^n}{r-1}-\frac{1}{r-1} \end{eqnarray}後半は定数なので、前半部分だけを考えればいいですね。

$r^n$ の極限は、【基本】等比数列の極限で見ましたね。 $r\gt 1$ のときは正の無限大に発散し、 $|r|\lt 1$ のときは収束し、 $r\leqq -1$ のときは振動するのでした。

$|r|\lt 1$ のとき、 $r^n$ は $0$ に収束するので、部分和の極限は
\begin{eqnarray} \lim_{n\to\infty} \frac{r^n-1}{r-1}=\frac{-1}{r-1}=\frac{1}{1-r} \end{eqnarray}となります。

数直線で表すと次のようになります。

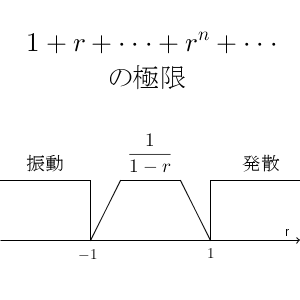
等比数列の極限とは、似ているけど少し違います（参考：【基本】等比数列の極限）。

無限等比級数の収束・発散を調べる

無限等比級数が収束するか発散するかは、公比に注意して考えていきます。

「無限等比級数」と書かれているので、まずは公比を考えます。

(1)は、公比が $\sqrt{2}$ であることがわかり、絶対値が $1$ 以上であることから、発散することがわかります。部分和を求める必要はありません。

(2)は、公比を $r$ とすると
\begin{eqnarray} r=\frac{2-\sqrt{2} }{\sqrt{2} }=\sqrt{2}-1 \end{eqnarray}となります。 $1\lt \sqrt{2}\lt 2$ なので、 $|r|\lt 1$ であることがわかります。よって、収束することがわかります。

極限値は、先ほど求めた値に初項を掛ければ求められます。和は
\begin{eqnarray} \sqrt{2}\times\frac{1}{1-r} &=& \frac{\sqrt{2} }{1-(\sqrt{2}-1)} \\[5pt] &=& \frac{\sqrt{2}(2+\sqrt{2})}{(2-\sqrt{2})(2+\sqrt{2})} \\[5pt] &=& \frac{2\sqrt{2}+2}{2} \\[5pt] &=& \sqrt{2}+1 \end{eqnarray}と求められます。収束する場合は $n$ 乗の部分が消えるので、項が有限の場合（ただの等比数列の和のこと）を考えるよりもスッキリしますね。

おわりに

ここでは、無限等比級数について見てきました。いつ収束・発散するか、収束するならその和はどのように書けるか、を見てきました。等比数列の収束とは少し状況が違うこともおさえておきましょう。