【標準】無限等比級数の収束条件

ここでは、文字を含んだ無限等比級数が、どのような場合に収束するか、を考えていきます。

無限等比級数の極限の復習

【基本】無限等比級数で見たように、\[ 1+r+r^2+r^3+\cdots \]という無限等比級数は、 $|r|\lt 1$ のときに収束します。このときの第 $n$ 項までの部分和は\[ \frac{1-r^n}{1-r} \]であり、 $|r|\lt 1$ なら数列 $\{r^n\}$ が0に収束するからですね。これ以外の場合は発散します。

より一般的な場合を考えてみましょう。初項が $a$ で公比が $r$ の場合、つまり、\[ a+ar+ar^2+ar^3+\cdots \]の場合、初項が $1$ のときと大きく異なるのは、初項が0の場合です。 $a=0$ なら、 $r$ が何であっても和は0になります。 $a\ne0$ なら、 $a=1$ のときと同じように、 $|r|\lt 1$ のときに収束し、極限は\[ \frac{a}{1-r} \]となります。 $a\ne 0$ かつ $|r|\geqq 1$ のときは発散します。

無限等比級数の収束について、一般的な場合でまとめておきましょう。

「 $a=0$ のときなんて当たり前すぎるから、考える必要はないのでは？」と思う人がいるかもしれません。もちろん、【基本】無限等比級数の後半で見たような、具体的な数字を使って無限等比級数の和を求めるような場合には、初項が0なんて問題が出題されることはありません。が、問題になるのは、文字を含んでいる無限等比級数の場合なんですね。次で見てみましょう。

文字を含んだ無限等比級数の収束条件

初項が $x$ で、公比が $1-x$ の無限等比級数です。ここで、「公比の絶対値が 1 以下なら収束するのだから、 $|1-x|\lt 1$ を解いて $0\lt x \lt 2$ だ」と答えると間違いなんですね。

先ほども考えた通り、初項が 0 の場合には、この無限等比級数は必ず収束します。なので、初項が0か0じゃないか、場合分けをして考えないといけません。文字の場合、0になることを忘れてしまいやすいので注意が必要です。

初項が0、つまり、 $x=0$ の場合は、収束し、和は $0$ となります。

初項が0でない場合、つまり、 $x\ne 0$ の場合は、公比 $1-x$ の絶対値が1より小さいときに収束するので、\[ |1-x|\lt 1 \]を解いて、\[ 0\lt x\lt 2 \]となります。また、和は、\[ \frac{x}{1-(1-x)}=1 \]となります。初項と公比から、無限等比級数の和をどう出すかは、先ほどの式に代入すればわかりますね。

よって、収束する範囲は $0\leqq x \lt 2$ となり、和は $x=0$ のときは $0$ で、 $0\lt x \lt 2$ のときは $1$ となります。

解答としてはこれでおしまいですが、この無限等比級数がどのように収束・発散していくか、最後に見てみましょう。

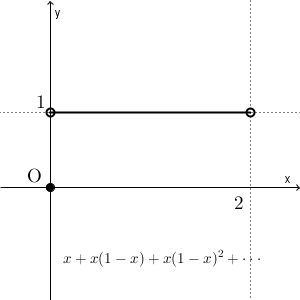
第 $n$ 項までの和を計算し、 $x$ の関数だと思ってグラフにし、 $n$ を11まで動かしたものが下の図です。

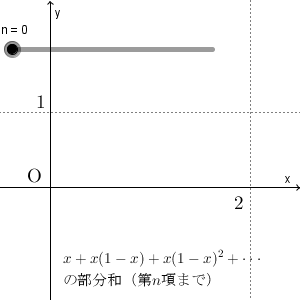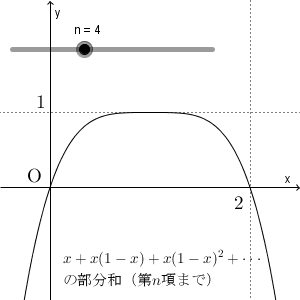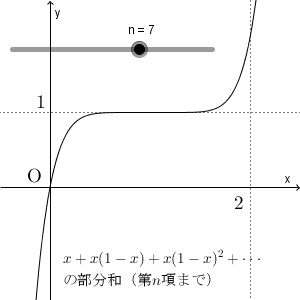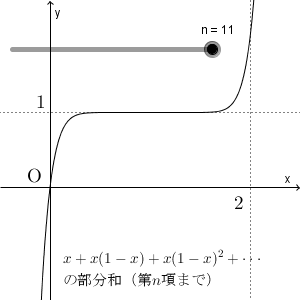
例えば、 $n=1$ なら $y=x$ で、 $n=2$ なら $y=x+x(1-x)$ としている、ということです。無限等比級数は、 $n\to\infty$ としたものですが、上の図はその途中までの様子を見ているわけですね。

上の図を見ると、 $x=0$ のときは、必ず $y=0$ となっており、 $x\lt 0$ の部分では、どんどん $y$ 軸に近づいていくことがわかります。

また、 $0\lt x \lt 2$ の部分では、 $y=1$ に近づいています。 $n$ がそんなに大きくないため、 $x=0,2$ 付近ではそんなに近づいていませんが、大きくするともっと近づいていきます。

また、 $x\geqq 2$ の範囲では、グラフは上下に振動していることがわかります。少しわかりづらいですが、 $x=2$ のときは、 $y=0$ と $y=2$ のときが交互に表れています。 $x\gt 2$ のときは、さらに振れ幅が大きくなります。

極限を考えると、 $x=0$ のときに $y=0$ 、 $0\lt x \lt 2$ のときに $y=1$ 、他は発散、となるのでしたね。部分和を考えている段階ではグラフはつながっていますが、収束する部分のみを抜き出してグラフにするとブチっと切れてしまうことがわかります。

極限を考える前に起こっていたこと（例えば、グラフがつながっていること）が、極限を考えた後でも成り立つかどうかはわかりません。このことは、極限や微分を学んでいくと、いろんなところで体験することになるでしょう。

おわりに

ここでは、文字を含んだ無限等比級数がいつ収束するか、を考えました。初項が0になるケースを忘れやすいので注意しましょう。