【基本】等比数列の極限

ここでは、等比数列の極限について考えていきます。どういうときに収束し、どういうときに発散するかを見ていきます。

等差数列・等比数列の復習

【基本】数列の極限では、数列の極限を考えるときに $a_n=\dfrac{1}{n}$ となる数列などを見てきました。ただ、数列の分野で見た、基本的な数列といえば、等差数列と等比数列でした。これらの数列の極限はどうなっているか、を考えてみましょう。

等差数列とは、差が一定の数列のことで、この差のことを公差というのでした（参考：【基本】等差数列）。初項が $a$ で、公差が $d$ の等差数列 $\{a_n\}$ の一般項は\[ a_n = a+(n-1)d \]で書けるのでした。この極限は、 $nd$ の部分だけが影響することがわかります。 $d$ が正なら、正の無限大に発散し、 $d$ が負なら、負の無限大に発散します。 $d=0$ なら $a$ に収束します。あまりおもしろくない結果です。

等比数列は、比が一定の数列のことで、この比を公比というのでした（参考：【基本】等比数列）。初項が $a$ で、公比が $r$ の等比数列 $\{a_n\}$ の一般項は\[ a_n = ar^{n-1} \]で書けるのでした。この極限を考えるのに一番大事な部分は、 $r^n$ の部分ですね。これは、公比によって、いろいろ結果が変わりそうです。

例えば、 $r=2$ としてみると、 $r^n$ は正の無限大に発散することがわかります。2倍ずつされていくのだから、限りなく大きくなっていきます。一方、 $r=\dfrac{1}{2}$ なら、半分ずつになっていくのだから、 $0$ に近づいていくことがわかります。この境目はどこかと考えると、増えていくことも減っていくこともない、 $r=1$ の場合である、と考えられます。

公比が負の場合は、また少し様子が異なります。例えば、 $r=-1$ としてみると、 $1$ と $-1$ とを繰り返すため、収束しません。振動します。また、 $r=-2$ などとすると、絶対値が大きくなりながら符号が変わるので、この場合も発散します。 $r=-\dfrac{1}{2}$ のときも符号が変わっていくのですが、絶対値はどんどん小さくなり、 $0$ に近づく、つまり、この場合は収束することがわかります。

ここまでのことを踏まえ、もう少し詳しく等比数列の極限について考えていきます。

等比数列の極限

先ほど見たように、等比数列の極限を考えるには、 $\{r^n\}$ の極限について調べればいいですね。ちなみに、これは、初項も公比も $r$ の等比数列です。

さて、先ほど見た通り、まずは $r\gt 1$ と $r=1$ の部分で状況が変わりそうなことがわかります。 $r\gt 1$ のときは、 $r=2$ のときなどを考えれば、どんどん大きくなっていくことが予想できます。ただ、 $r=1.00\cdots 01$ のように、すごく1に近い場合でも、本当にどんどん大きくなっていくか、は少し怪しいかもしれません。

このことを確かめるには、 $r=1+h$ とおいて、二項定理を使ってみるとはっきりします（参考：【標準】n乗の展開と二項定理）。 $r\gt 1$ だから $h\gt 0$ なので、
\begin{eqnarray} r^n &=& (1+h)^n \\[5pt] &=& {}_n \mathrm{ C }_n +{}_n \mathrm{ C }_{n-1} h +{}_n \mathrm{ C }_{n-2} h^2 +\cdots \\[5pt] & & \cdots +{}_n \mathrm{ C }_{k} h^{n-k} +\cdots +{}_n \mathrm{ C }_1 h^{n-1} +{}_n \mathrm{ C }_0 h^n \\[5pt] & \geqq & 1+nh \end{eqnarray}となります。二項定理を使って展開した後の式で、 $1+nh$ 以外の項はすべて正なので、\[ r^n\geqq 1+nh \]となるんですね。こうすると、 $h$ がすごく0に近い値でも、正であれば、 $n$ を大きくすると右辺は限りなく大きくなることがわかります。よって、このときに $r^n$ は正の無限大に発散することがわかります。

ちなみに、上のようにして、正の無限大に発散することを示すために、二項定理を使う手法 はよく使われます。

$r=1$ のときは、 $r^n=1$ ですね。収束します。

$|r|\lt 1$ のときを考えてみましょう。 $r=0$ のときは $r^n=0$ です。 $r\ne 0$ のときは、 $s=\dfrac{1}{|r|}$ とおくと、 $s\gt 1$ なので、 $s^n$ は正の無限大に発散することがわかります。よって、 $|r^n|=\dfrac{1}{s^n}$ は0に収束するので、 $r^n$ は0に収束することがわかります。

$r=-1$ のときは、 $r^n$ は $1,-1$ の値を交互にとるため、振動します。

$r\lt -1$ のときは、 $|r|\gt 1$ なので、 $|r^n|$ は正の無限大に発散します。また、符号は交互に変わるので、この場合も振動します。

以上から、等比数列 $\{r^n\}$ の極限は、次のようにまとめられます。

特に、数列 $\{r^n\}$ が収束することは、 $-1\lt r \leqq 1$ と同値であることがわかります。このことも重要です。

数直線で分けると、次のようになります。

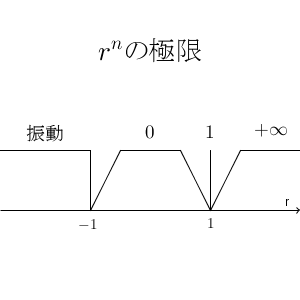
どこが境目になるか、自然と思いつけるようになっておきましょう。値がどう変化していくかを、イメージできるようになっておきましょう。 $r^n$ という形を見て、勝手に「発散する」とか「収束する」などと思い込まないようにしましょう。

おわりに

ここでは、主に、等比数列の極限について、見てきました。どこが境目になるかを頑張って覚えるのではなく、値の変化のイメージと関連付けて考えられるようになっておくといいでしょう。後で、これとよく似たものが出てくる（無限等比級数の極限のところ）ので、単純な暗記で乗り切ると、後で混乱してしまうかもしれません。