【基本】サイクロイドと媒介変数表示

🕒 2018/06/02 🔄 2023/05/01

ここでは、円が直線に接しながら回転するときに、円周上の定点が描く曲線、サイクロイドについて、媒介変数表示がどうなるかを見ていきます。

📘 目次

サイクロイド

媒介変数表示の例として、楕円や双曲線などの二次曲線の媒介変数表示を扱ってきました（参考：【基本】楕円と媒介変数表示）が、ここでは、 $x,y$ の方程式ではきれいに書けないけれど、媒介変数表示ではきれいに書ける例として、サイクロイドについて見ていきます。

サイクロイドは、円が直線に接しながら滑ることなく回転するときに、円周上のある点が描く曲線のことです。具体的に見てみましょう。

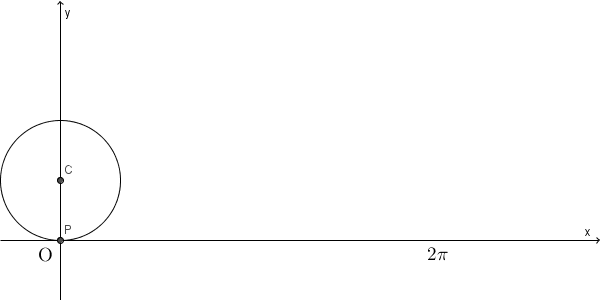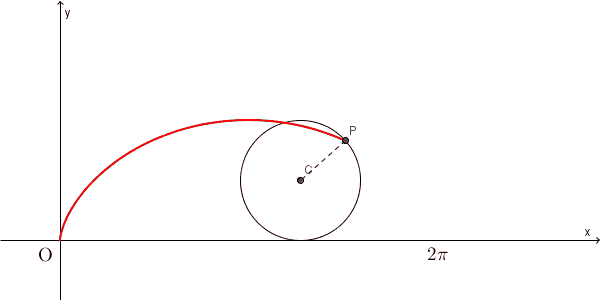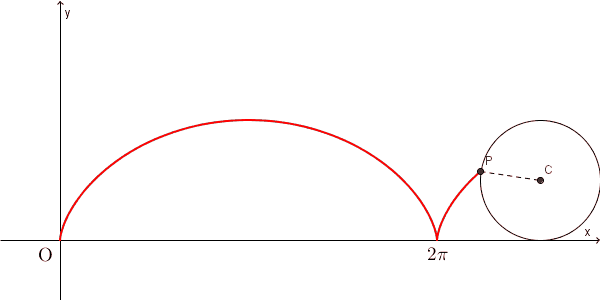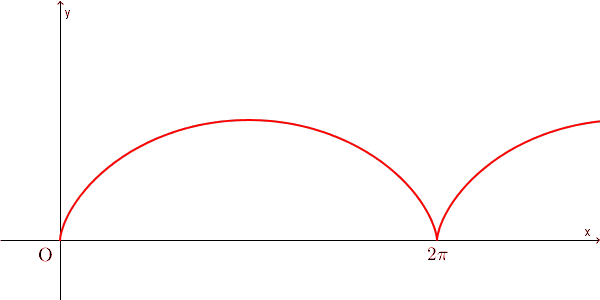
上の図では、半径 $1$ の円が x 軸と原点で接しているところからスタートしています。その後、 x 軸に接しながら、滑ることなく回転していっています。半径の動きを見れば、回転していることがわかります。

このとき、もともと x 軸と接していた点は、ある曲線を描きます。この曲線のことをサイクロイド(cycloid) といいます。

この曲線は、円の一部や放物線の一部などではなく、今までには出てこなかった曲線です。

サイクロイドの媒介変数表示

サイクロイドは、 $x,y$ を使ったきれいな式で書くことはできません。しかし、媒介変数表示ならスッキリと書くことができます。ここでも、半径1の円が x 軸上を転がる前提で考えていきます。

ところで、上の図から分かる人もいると思いますが、円が1回転したあと、円はどの位置にいるでしょうか。原点と接していた点がもう一度 x 軸と接するときを考えてみましょう。この移動距離は、この円の円周と等しくなりますね。つまり、 $2\pi$ だけ横に移動していることがわかります。

このように、円がどれだけ回転したかと、円がどれだけ移動したかが関係している、ということを利用するのがポイントです。

上の図のような状況を考えてみましょう。転がり始めてすぐのところで止めています。点 C は円の中心で、点 P はもともと原点にあった点です。この点の軌跡をサイクロイドというのでしたね。 A は円と x 軸との接点です。

先ほどもかきましたが、円がどれだけ移動したか、つまり、 OA の長さ、さらに言い換えれば C の x 座標は、弧 AP と同じ長さになります。滑らずに回転しているので、円の移動と円の回転が関連しているわけですね。

$\angle \mathrm{ ACP }=\theta$ とする（弧度法を使います）と、弧 AP の長さは $\theta$ なので、 C の座標は、 $(\theta,1)$ となることがわかります。

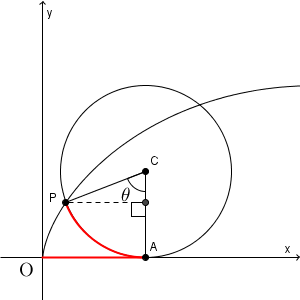
さらに、C と P との位置関係を見れば、点 P の座標 $(x,y)$ は
\begin{eqnarray} x &=& \theta -\sin\theta \\[5pt] y &=& 1 -\cos\theta \\[5pt] \end{eqnarray}となることがわかります。これは、 $\theta$ が $\dfrac{1}{2}\pi$ 以上になっても成り立ちます。よって、これは、サイクロイドの媒介変数表示となっています。

なお、半径が $1$ ではなく $a$ になった場合は、 C の座標も P の座標も a 倍すればいいだけなので、
\begin{eqnarray} x &=& a(\theta -\sin\theta) \\[5pt] y &=& a(1 -\cos\theta) \\[5pt] \end{eqnarray}となります。

$\sin,\cos$ だけの式なら相互関係を用いて $x,y$ の関係式できれいに書けるかもしれませんが、 x 座標に $\theta$ そのものが入っています。そのため、この式から、きれいに $x,y$ の関係式を表すことはできません。媒介変数表示を用いないと、表すことは難しいです。