【基本】円と直線の共有点(中心からの距離に注目)
ここでは、円と直線の共有点の個数について見ていきます。中心からの距離に注目して求めます。
円と直線の共有点の個数
【基本】円と直線の共有点(二次方程式に注目)では、共有点の座標を求めるために、直線の方程式を円の方程式に代入し、得られた二次方程式を解きました。また、この判別式を使えば、共有点の個数を求めることもできました。
ただ、共有点の個数を求めるだけなら、別の方法もあります。円の中心からの距離に着目して考えてみましょう。
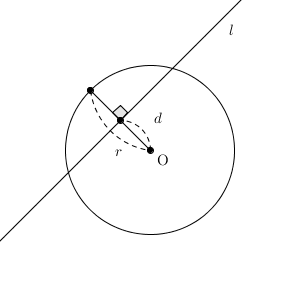
上の図は、円 O と直線 l の共有点が2点あるときを表しています。半径が r で、円の中心から直線までの距離を d としています。
共有点が2点ある場合、中心から直線に下した垂線の足は、円の内部にあるため、 $d\lt r$ となります。逆に $d\lt r$ なら、直線の一部が円の内部にあるということなので、円と直線の共有点は2点となります。
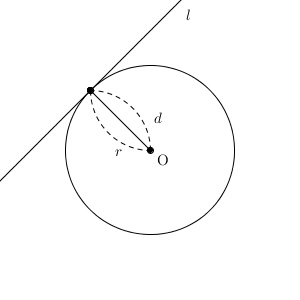
$d=r$ のときは、共有点が1点となります。逆に、共有点が1点の場合は、直線が円の接線になっていて、 $d=r$ となることがわかります。
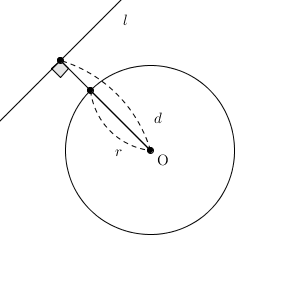
$d\gt r$ のときは、「円の中心と直線上の点との一番近い距離」でさえ半径より大きいのだから、直線上の点は円の外側にあります。よって、共有点はありません。また、共有点がないときは、 $d\gt r$ でないといけません。
以上のことから、次のようにまとめることができます。
- $d\lt r$ $\iff$ 共有点は2点
- $d = r$ $\iff$ 共有点は1点
- $d\gt r$ $\iff$ 共有点はなし
ちなみに、円の中心から直線までの距離は、【標準】点と直線との距離で見た内容が使えます。これを使えば、計算はかなり楽になります。
例題
(1) $y=x$
(2) $y=x+2$
(3) $y=x+4$
【基本】円と直線の共有点(二次方程式に注目)と同じ設定ですが、共有点の個数だけなので、上で見た内容を使いましょう。
円の中心は原点で、半径は $\sqrt{2}$ です。原点と各直線との距離をそれぞれ求め、半径と比べましょう。
(1) は $x-y=0$ と変形できるため、原点との距離は $0$ です。 $0\lt \sqrt{2}$ なので、共有点は2点です。
(2) は $x-y+2=0$ と変形できるため、原点との距離は \[ \frac{2}{\sqrt{1^2+(-1)^2} }=\sqrt{2} \] です。半径と等しいので、共有点は1点です。
(3) は、 $x-y+4=0$ と変形できるため、原点との距離は \[ \frac{4}{\sqrt{1^2+(-1)^2} }=2\sqrt{2} \] です。 $2\sqrt{2}\gt \sqrt{2}$ なので、共有点はなしです。
二次方程式を考えるよりも、だいぶ計算が楽になりましたね。原点が中心だったから計算が楽になった面もありますが、原点以外の場合でも、点と直線との距離の公式の分子の計算が少し増えるだけで、そんなに計算量は増えないでしょう。
おわりに
ここでは、円の中心から直線までの距離に着目して、円と直線の共有点の個数を考えました。共有点の座標まではわかりませんが、共有点の個数だけならこの方法で求める方が楽でしょう。





