【基本】y軸とで囲まれた部分の面積と積分

ここでは、 $x=g(x)$ と $y$ 軸とで囲まれた部分の面積と積分についてみていきます。

y軸とで囲まれた部分の面積と積分

【基本】x軸とで囲まれた部分の面積と積分で見たように、 $a\leqq x\leqq b$ で $f(x)\geqq 0$ のとき、 $y=f(x)$ と $x=a$, $x=b$, $x$ 軸で囲まれた部分の面積は\[ \int_a^b f(x)dx \]で表すことができます。

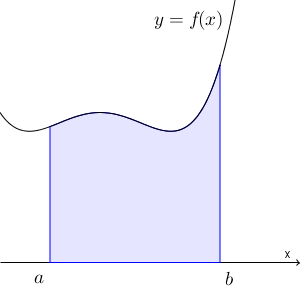
これと関連して、縦と横を入れ替えたものも、同じように計算することができます。次の図を見てみましょう。

このような $x=g(y)$ について考えます。 $c\leqq x\leqq d$ の区間で、 $g(y)\geqq 0$ だとすると、 $x=g(y)$ と、 $y=c$, $y=d$, $y$ 軸で囲まれた部分の面積は、\[ \int_c^d g(y)dy \]で表すことができます。縦と横を入れ替えただけですね。

積分を使って面積を求める

グラフは次のようになります。

先ほど見たように、 $y$ についての積分だと考えて計算してみましょう。

$y=\log x$ を $x=$ の形に変形すると、 $x=e^y$ となります。よって、 $S$ は次のようにして求めることができます。
\begin{eqnarray} S &=& \int_0^1 e^y dy \\[5pt] &=& \Big[ e^y \Big]_0^1 \\[5pt] &=& e-1 \end{eqnarray}これが答えです。

ただ、別の解き方として、次のように、長方形から不要な部分を引く、という方法もあるでしょう。

長方形の面積は、 $e$ ですね。これは積分するまでもありませんが、あえて積分を使って書くなら、\[ \int_0^e dx \]となります。ここから、 $y=\log x$ と $x=e$, $x$ 軸で囲まれた部分の面積を引けばいいので、この部分の面積を求めましょう。 $\log$ の積分は、部分積分を使わないといけません（参考：【基本】定積分の部分積分の計算（logの定積分など））。
\begin{eqnarray} & & \int_1^e \log x dx \\[5pt] &=& \Big[ x\log x \Big]_1^e-\int_1^e x\cdot \frac{1}{x} dx \\[5pt] &=& (e\cdot 1-1\cdot 0)-\Big[ x \Big]_1^e \\[5pt] &=& e-(e-1)=1 \end{eqnarray}このように求められるので、\[ S=e-1 \]であることがわかります。

また、もし、 $y$ について積分するのが考えづらいということであれば、関数などをまとめて、縦と横を入れ替えてしまう方法もあります。つまり、直線 $y=x$ について反転させるわけですね。

反転させても面積は変わりません。結果的に、 $y=e^x$ と $x$ 軸、 $y$ 軸、 $x=1$ で囲まれた部分の面積の面積を求めることになります。このように考えれば\[ \int_0^1 e^x dx \]を計算することになりますが、これは1番初めに見たのと実質的に同じ計算をすることになります。積分変数が $y$ から $x$ に変わっただけですね。

面積を求めるときには、このように $y=x$ について反転したり、平行移動したり、回転移動をして、積分が計算しやすくなるような移動を事前に行うこともあります。

おわりに

ここでは、 $x=g(y)$ と $y$ 軸とで囲まれた部分の面積を、積分を使って計算する方法を見てきました。 $y$ について積分するか、図形全体を $y=x$ について反転させて $x$ について積分することで、求められましたね。また、求めたい箇所を含んだ部分から、不要な部分を引くことで、求めたい面積を計算する方法も見ました。積分の計算は、やり方によってすごく複雑になったり簡単になったりするので、いろいろな求め方ができるようになっていきましょう。