【基本】x軸とで囲まれた部分の面積と積分
ここでは、 $y=f(x)$ と $x$ 軸とで囲まれた部分の面積と積分についてみていきます。
面積と積分
【基本】不定積分の復習#積分ってなんでやるんだっけでも書きましたが、積分を考える主な理由の一つに、「面積が求められる」というものがあります。このことについて少し考えましょう。
話としては、【基本】面積と整式の不定積分の内容と同じです。単に、考えている関数が増えているだけです。
$f(x)$ を連続な関数とします。また、 $a\leqq x \leqq b$ で $f(x)\geqq 0$ とします。このとき、 $y=f(x)$ と $x=a$, $x=b$, x 軸で囲まれた部分の面積を考えてみましょう。
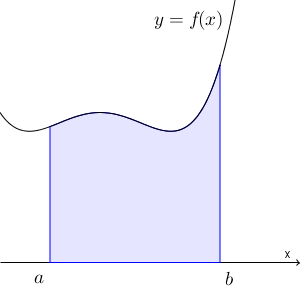
$a\leqq c \leqq b$ とし、 $x=c$ までの部分の面積を $S(c)$ という関数で表すとします。このとき、 $h\gt 0$ とすると、 $\dfrac{S(c+h)-S(c)}{h}$ は、 $c\leqq x \leqq c+h$ での最小値以上、最大値以下となることがわかります。

小さい長方形以上、大きい長方形以下、ということですね。
$h\to 0$ とすると、区間が小さくなるにつれ、最小値も最大値も $f(c)$ に近づいていきます。また、 $h\lt 0$ のときも同様です。
このことから、\[ \lim_{h\to 0} \frac{S(c+h)-S(c)}{h}=f(c) \]が成り立つこと、つまり、 $S'(c)=f(c)$ であることがわかります。よって、 $a\leqq x \leqq b$ のときは $S'(x)=f(x)$ となるので、この範囲では、「面積 $S(x)$ は、関数 $f(x)$ の不定積分の1つだ」と言えます。
ここで、 $F(x)=\int f(x) dx$ とすると、両方とも不定積分なので、\[ S(x)=F(x)+C \]となります(C は定数)。 $x=a$ での面積は $0$ なので、
\begin{eqnarray}
0 &=& F(a)+C \\
C &=& -F(a) \\
\end{eqnarray}となります。よって、 $y=f(x)$ と $x=a$, $x=b$, x 軸で囲まれた部分の面積は、
\begin{eqnarray}
S(b)=F(b)+C=F(b)-F(a)
\end{eqnarray}と書くことができることがわかります。
以上から、 $a\leqq x\leqq b$ のときに、 $f(x)\geqq 0$ であれば、 $y=f(x)$ と $x$ 軸、そして、 $x=a$, $x=b$ で囲まれた部分の面積は、定積分を使って\[ \int_a^b f(x) dx \]で表すことができることがわかります。
また、もしこの範囲で $f(x)\leqq 0$ であれば、面積は\[ -\int_a^b f(x) dx \]で書けます。上下を反転させて考えればいいですね。
もし $a\leqq x\leqq b$ の範囲で、 $f(x)$ が正になることも負になることもあるとすると、その場合には、積分区間をわけてそれぞれを足し合わせればいいです。簡潔に書けば、\[ \int_a^b |f(x)| dx \]ということです。
積分を使って面積を求める
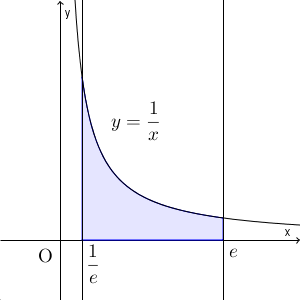
$\dfrac{1}{e}\leqq x\leqq e$ のとき、 $y=\dfrac{1}{x}$ はつねに正なので、上で見たことから
\begin{eqnarray}
S
&=&
\int_{\frac{1}{e} }^e \dfrac{1}{x} dx \\[5pt]
&=&
\Big[ \log x \Big]_{\frac{1}{e} }^e \\[5pt]
&=&
\log e -\log\frac{1}{e} \\[5pt]
&=&
2
\end{eqnarray}となります。
おわりに
ここでは、 $y=f(x)$ と $x$ 軸、 $x=a$, $x=b$ で囲まれた部分の面積を求めるには、定積分を計算すればいいことを見ました。 $y=f(x)$ のグラフが $x$ 軸より上にあるか下にあるかによって、積分の符号が異なります。そのため、面積を考えるには、 $y=f(x)$ のグラフと $x$ 軸との位置関係を把握する必要がある点に注意しましょう。





