東京大学 理系 2013年度 第6問 解説
問題編
問題
座標空間において、 $xy$ 平面内で不等式 $|x|\leqq 1$, $|y|\leqq 1$ により定まる正方形 $S$ の4つの頂点を $\mathrm{A}(-1,1,0)$, $\mathrm{B}(1,1,0)$, $\mathrm{C}(1,-1,0)$, $\mathrm{D}(-1,-1,0)$ とする。正方形 $S$ を、直線 BD を軸として回転させてできる立体を $V_1$ 、直線 AC を軸として回転させてできる立体を $V_2$ とする。
(1) $0\leqq t\lt 1$ を満たす実数 $t$ に対し、平面 $x=t$ による $V_1$ の切り口の面積を求めよ。
(2) $V_1$ と $V_2$ の共通部分の体積を求めよ。
考え方
図形自体はわかりやすいのですが、切り口がどうなるかを式で表すのは大変です。式で表すことさえできれば、積分の計算は大変ではないのですが、式で表すところまではなかなかたどりつけません。
(2)は(1)ができればすぐにできる、というわけではないですが、(1)が解ける実力があれば(2)もできるでしょう。
解答編
問題
座標空間において、 $xy$ 平面内で不等式 $|x|\leqq 1$, $|y|\leqq 1$ により定まる正方形 $S$ の4つの頂点を $\mathrm{A}(-1,1,0)$, $\mathrm{B}(1,1,0)$, $\mathrm{C}(1,-1,0)$, $\mathrm{D}(-1,-1,0)$ とする。正方形 $S$ を、直線 BD を軸として回転させてできる立体を $V_1$ 、直線 AC を軸として回転させてできる立体を $V_2$ とする。
(1) $0\leqq t\lt 1$ を満たす実数 $t$ に対し、平面 $x=t$ による $V_1$ の切り口の面積を求めよ。
解答
(1)
$V_1$ は、2つの円錐をくっつけた立体となる。
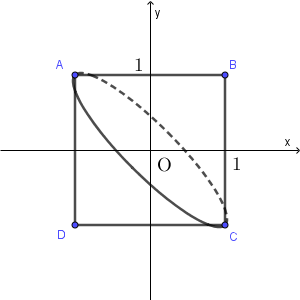
$V_1$ を平面 $y=-x+2s$ $(0\leqq s\lt 1)$ で切ると、断面は点 $(s,s,0)$ を中心とした半径 $\sqrt{2}(1-s)$ の円となる。(次の図は $z$ 軸方向から見た図)
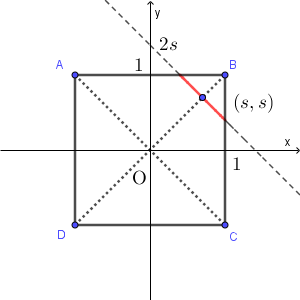
これは、点 $(s,s,0)$ を中心とした半径 $\sqrt{2}(1-s)$ の球を平面 $y=-x+2s$ で切ったときの断面と等しいので、この断面上にある点 $(x,y,z)$ は次の2つの式を満たす。
\begin{eqnarray}
& & y=-x+2s \\[5pt]
& & (x-s)^2+(y-s)^2+z^2 \leqq 2(1-s)^2
\end{eqnarray}
この断面をさらに平面 $x=t$ で切ると、その断面上の点は、次の2つの式を満たす。
\begin{eqnarray}
& & y=-t+2s \\[5pt]
& & (t-s)^2+(y-s)^2+z^2 \leqq 2(1-s)^2
\end{eqnarray}1つ目の式より、 $2s=y+t$ であるから、これを2つ目の式へ代入すると
\begin{eqnarray}
(t-s)^2+(y-s)^2+z^2 & \leqq & 2(1-s)^2 \\[5pt]
t^2-2ts+y^2-2ys+z^2 & \leqq & 2-4s \\[5pt]
t^2+y^2-2s(y+t)+z^2 & \leqq & 2-4s \\[5pt]
t^2+y^2-(y+t)^2+z^2 & \leqq & 2-2(y+t) \\[5pt]
-2ty+z^2 & \leqq & 2-2y-2t \\[5pt]
(2-2t)y & \leqq & -z^2+2-2t \\[5pt]
y & \leqq & \frac{z^2}{2t-2}+1 \\[5pt]
\end{eqnarray}が得られる。よって、 $V_1$ の点 B を含む方の円錐を平面 $x=t$ で切断すると、断面の境界線には放物線 $y=\dfrac{z^2}{2t-2}+1$ の一部が現れる。
また、 $2s=y+t$ で $0\leqq s\lt 1$ だから
\begin{eqnarray}
0\leqq y+t \lt 2 \\[5pt]
-t \leqq y \lt 2-t \\[5pt]
\end{eqnarray}となる。 $0\leqq t\lt 1$ なので、 $2-t\gt 1$ となる。 $y=-t$ のとき
\begin{eqnarray}
-t &=& \dfrac{z^2}{2t-2}+1 \\[5pt]
-t-1 &=& \dfrac{z^2}{2t-2} \\[5pt]
2(1-t^2) &=& z^2 \\[5pt]
z &=& \pm\sqrt{2(1-t^2)} \\[5pt]
\end{eqnarray}となる。これより、 B を含む方の円錐を平面 $x=t$ で切断したときの断面は次の図の色のついた部分となる。
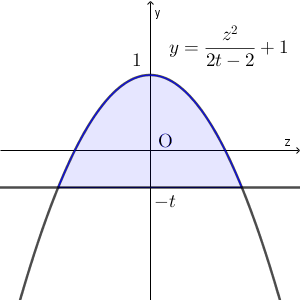
$V_1$ の点 D を含む方の円錐を平面 $x=t$ で切ったときの切断面は、図形の対称性から、 B を含む方の立体を平面 $x=-t$ で切ったときの切断面と同じ形になる。
以上から、 $a=\sqrt{2(1-t^2)}$ とおくと、求める面積は
\begin{eqnarray}
& &
\int_{-a}^a \left(\frac{z^2}{2t-2}+1\right) dz \\
& & +\int_{-a}^a \left(\frac{z^2}{2(-t)-2}+1\right) dz \\[5pt]
&=&
\int_{-a}^a \left(\frac{z^2}{2(t-1)}+1 -\frac{z^2}{2(t+1)}+1\right) dz \\[5pt]
&=&
\int_{-a}^a \left(\frac{z^2\left\{(t+1)-(t-1)\right\} }{2(t^2-1)}+2\right) dz \\[5pt]
&=&
\int_{-a}^a \left(\frac{z^2}{t^2-1}+2\right) dz \\[5pt]
&=&
2\int_0^a \left(\frac{z^2}{t^2-1}+2\right) dz \\[5pt]
&=&
2\left[ \frac{z^3}{3(t^2-1)}+2z \right]_0^a \\[5pt]
&=&
2\left\{ \frac{2(1-t^2)\sqrt{2(1-t^2)} }{3(t^2-1)}+2\sqrt{2(1-t^2)} \right\} \\[5pt]
&=&
2\left\{ -\frac{2\sqrt{2(1-t^2)} }{3}+2\sqrt{2(1-t^2)} \right\} \\[5pt]
&=&
2\cdot \frac{4\sqrt{2(1-t^2)} }{3} \\[5pt]
&=&
\frac{8\sqrt{2(1-t^2)} }{3} \\[5pt]
\end{eqnarray}となる。
((1)終)
解答編 つづき
問題
(2) $V_1$ と $V_2$ の共通部分の体積を求めよ。
解答
(2)
$V_1$ の点 D を含む側の円錐を平面 $x=t$ で切断したときの断面は、図形の対称性から、 $V_1$ の点 B を含む側の円錐を平面 $x=-t$ で切断したときの断面を $xz$ 平面について対称移動したものになるので、次の図の色のついた部分となる。
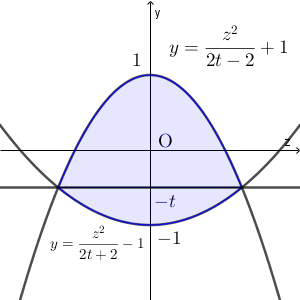
式で表すと、次の2つの不等式を満たす範囲である。
\begin{eqnarray}
\left\{
\begin{array}{l}
y \leqq \dfrac{z^2}{2t-2}+1 \\[5pt]
y \geqq -\left(\dfrac{z^2}{2(-t)-2}+1\right) = \dfrac{z^2}{2t+2}-1
\end{array}
\right.
\end{eqnarray}
$V_1$ と $V_2$ は $xz$ 平面について対称なので、 $V_2$ を平面 $x=t$ で切断したときの断面は、 $V_1$ を平面 $x=t$ で切断したときの断面を $xz$ 平面について対称移動したものとなる。なので、断面は次の2つの不等式を満たす範囲である。
\begin{eqnarray}
\left\{
\begin{array}{l}
y \leqq -\dfrac{z^2}{2t+2}+1 \\[5pt]
y \geqq -\dfrac{z^2}{2t-2}-1
\end{array}
\right.
\end{eqnarray}
$0\leqq t \lt 1$ のとき、 $y\geqq 0$ の範囲では、
\begin{eqnarray}
& &
\left(-\frac{z^2}{2t+2}+1\right)-\left(\frac{z^2}{2t-2}+1\right) \\[5pt]
&=&
-\frac{z^2}{2t+2}+\frac{z^2}{2-2t} \\[5pt]
&\geqq &
0
\end{eqnarray}となる。よって、 $V_1$, $V_2$ の共通部分を平面 $x=t$ で切断したときの断面は次のようになる。
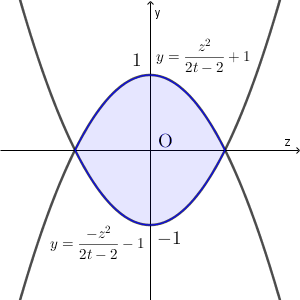
なお、 $0=\dfrac{z^2}{2t-2}+1$ とすると $z=\pm\sqrt{2-2t}$ なので、 $a=\sqrt{2-2t}$ とおくと、この断面の面積は
\begin{eqnarray}
& &
2\int_{-a}^{a} \left(\frac{z^2}{2t-2}+1\right) dz \\[5pt]
&=&
4 \left[ \frac{z^3}{3(2t-2)}+z \right]_0^a \\[5pt]
&=&
4 \left\{ \frac{(2-2t)\sqrt{2-2t} }{3(2t-2)}+\sqrt{2-2t} \right\} \\[5pt]
&=&
4 \left( -\frac{\sqrt{2-2t} }{3}+\sqrt{2-2t} \right) \\[5pt]
&=&
\frac{8\sqrt{2-2t} }{3} \\[5pt]
\end{eqnarray}となる。
$x\leqq 0$ の部分の体積は $x\geqq 0$ の部分の体積と等しいので、共通部分の体積は
\begin{eqnarray}
& &
2 \int_0^1 \frac{8\sqrt{2-2t} }{3} dt \\[5pt]
&=&
2 \cdot \frac{8}{3} \left[ (2-2t)^{\frac{3}{2} }\cdot\frac{2}{3}\cdot \left(-\frac{1}{2}\right) \right]_0^1 \\[5pt]
&=&
\frac{16}{3} \cdot 2^{\frac{3}{2} } \cdot\frac{1}{3} \\[5pt]
&=&
\frac{32\sqrt{2} }{9} \\[5pt]
\end{eqnarray}となる。
((2)終)





