東京大学 理系 2013年度 第2問 解説
問題編
問題
$a$ を実数とし、 $x\gt 0$ で定義された関数 $f(x)$, $g(x)$ を次のように定める。
\begin{eqnarray} f(x) &=& \dfrac{\cos x}{x} \\[5pt] g(x) &=& \sin x+ax \\[5pt] \end{eqnarray} このとき $y=f(x)$ のグラフと $y=g(x)$ のグラフが $x\gt 0$ において共有点をちょうど3つ持つような $a$ をすべて求めよ。
考え方
グラフの共有点の個数を考えるのは、よくある設定です。ただ、関数をどのように変形するかが問題です。共有点が考えやすくなるように変形しないといけません。
解答編
問題
$a$ を実数とし、 $x\gt 0$ で定義された関数 $f(x)$, $g(x)$ を次のように定める。
\begin{eqnarray} f(x) &=& \dfrac{\cos x}{x} \\[5pt] g(x) &=& \sin x+ax \\[5pt] \end{eqnarray} このとき $y=f(x)$ のグラフと $y=g(x)$ のグラフが $x\gt 0$ において共有点をちょうど3つ持つような $a$ をすべて求めよ。
解答
$f(x)=g(x)$ とすると\[ \frac{\cos x}{x^2}-\frac{\sin x}{x}=a \]となる。この左辺を $h(x)$ とおくと、 $x\gt 0$ における $y=h(x)$ と $y=a$ のグラフの共有点がちょうど3つとなる場合を考えればよい。
\begin{eqnarray} h'(x) &=& \frac{-x^2\sin x -2x\cos x}{x^4}-\frac{x\cos x-\sin x}{x^2} \\[5pt] &=& \frac{-x\sin x-2\cos x}{x^3}-\frac{x^2\cos x-x\sin x}{x^3} \\[5pt] &=& \frac{-(x^2+2)\cos x}{x^3} \\[5pt] \end{eqnarray}となるので、 $h'(x)=0$ となるのは\[ x=\dfrac{\pi}{2}+n\pi \]のとき( $n$ は $0$ 以上の整数)。このとき \begin{eqnarray} & & h\left(\dfrac{\pi}{2}+n\pi\right) \\[5pt] &=& -\frac{\sin \left(\dfrac{\pi}{2}+n\pi\right)}{\dfrac{\pi}{2}+n\pi} \\[5pt] &=& -\frac{(-1)^n\cdot 2}{(2n+1)\pi} \\[5pt] \end{eqnarray}となる。この絶対値は、 $n$ について狭義単調減少である。これより、増減表は次のようになる。
\begin{array}{c|cccccccccc}
x & 0 & \cdots & \frac{1}{2}\pi & \cdots & \frac{3}{2}\pi & \cdots & \frac{5}{2}\pi & \cdots & \frac{7}{2}\pi & \cdots \\
\hline
f'(x) & & - & 0 & + & 0 & - & 0 & + & 0 & \\
\hline
f(x) & \times & \searrow & -\frac{2}{\pi} & \nearrow & \frac{2}{3\pi} & \searrow & -\frac{2}{5\pi} & \nearrow & \frac{2}{7\pi} &
\end{array}また、\[ \lim_{x\to +0} h(x)=\infty,\ \lim_{x\to \infty} h(x)=0 \]なので、 $y=h(x)$ のグラフは次のようになる。
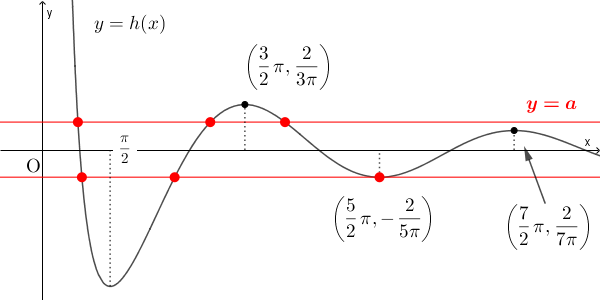
以上より、 $y=a$ との共有点がちょうど3つとなるのは、\[ \frac{2}{7\pi}\lt a\lt\frac{2}{3\pi},\ a=-\dfrac{2}{5\pi} \]のとき。
(解答終)
解説
$y=\dfrac{\cos x}{x}-\sin x$ と $y=ax$ に分けてしまうと、共有点の個数を考えるのが難しくなってしまいます。 $y=\cos x-x\sin x$ と $y=ax^2$ と分ければ、微分は楽になりますが、これも共有点の個数を考えるのは難しくなります。 $y=a$ との共有点を考えるように変形した方が安全でしょう。微分しにくくなるような変形なので少し抵抗はありますが、計算していくとこれがベストだとわかります。





