東京大学 理系 2013年度 第5問 解説
問題編
問題
次の命題P を証明したい。
命題P 次の条件(a), (b)をともに満たす自然数(1以上の整数)A が存在する。
(a) A は連続する3つの自然数の積である。
(b) A は10進数で表したとき、1が連続して99回以上現れるところがある。以下の問いに答えよ。
(1) y を自然数とする。このとき不等式\[ x^3+3yx^2 \lt (x+y-1)(x+y)(x+y+1) \lt x^3+(3y+1)x^2 \]が成り立つような正の実数 x の範囲を求めよ。
(2) 命題P を証明せよ。
考え方
「1が連続して99回」という、見ただけで避けてしまいたくなるような問題ですね。ノーヒントだとお手上げですが、(1)があるのでなんとか示せます。
(1)は、左側の不等号は常に成り立ちます。問題としては、少し気持ち悪いですね。右側は、二次関数の問題です。 $y=1$ のときに気を付けて解答を書きましょう。
(2)は(1)を使って、具体的に A を作り出します。(1)の中辺を見ると、連続する3つの自然数の積に対応していることに気づくでしょう。「1が連続して99回以上現れる」を言うには、(1)の左辺と右辺がどうなればいいか、を考えます。そこから、 x, y を具体的に決め、それらの値が(1)で求めた条件を満たすかどうかを確認します。答えは1つではないので、自分の扱いやすい数字で示しましょう。
解答編
問題
次の命題P を証明したい。
命題P 次の条件(a), (b)をともに満たす自然数(1以上の整数)A が存在する。
(a) A は連続する3つの自然数の積である。
(b) A は10進数で表したとき、1が連続して99回以上現れるところがある。以下の問いに答えよ。
(1) y を自然数とする。このとき不等式\[ x^3+3yx^2 \lt (x+y-1)(x+y)(x+y+1) \lt x^3+(3y+1)x^2 \]が成り立つような正の実数 x の範囲を求めよ。
解答
不等式の中辺は、次のように計算できる。
\begin{eqnarray}
& &
(x+y-1)(x+y)(x+y+1) \\
&=&
(x+y)\{(x+y)^2-1\} \\
&=&
(x+y)^3-(x+y) \\
&=&
x^3+3x^2y+3xy^2+y^3-x-y
\end{eqnarray}
よって、中辺から左辺を引くと
\begin{eqnarray}
& &
(x+y-1)(x+y)(x+y+1) -(x^3+3yx^2) \\
&=&
3xy^2+y^3-x-y \\
&=&
(3y^2-1)x +(y^2-1)y \\
\end{eqnarray}となる。 y は自然数なので、 $3y^2-1 \gt 0$ と $(y^2-1)y \geqq 0$ が成り立つ。よって、 x が正なら、つねに「(中辺)>(左辺)」が成り立つ。
一方、右辺から中辺を引くと
\begin{eqnarray}
& &
\{ x^3+(3y+1)x^2 \} -(x+y-1)(x+y)(x+y+1) \\
&=&
x^2 -3xy^2 -y^3 +x +y \\
&=&
x^2 +(-3y^2+1)x +(1-y^2)y \\
\end{eqnarray}となる。最後の式を $f(x)$ とおく。 $(1-y^2)y\leqq 0$ なので、 $z=f(x)$ のグラフは、 z軸と $z\leqq 0$ の範囲で交わる。また、 $3y^2-1 \gt 0$ なので、 $z=f(x)$ のグラフの軸は、 z 軸よりも右側にある。以上から、 $z=f(x)$ のグラフは x 軸と2か所で交わり、片方は $x\gt 0$ の部分で、もう片方は $x\leqq 0$ の部分で交わることがわかる。
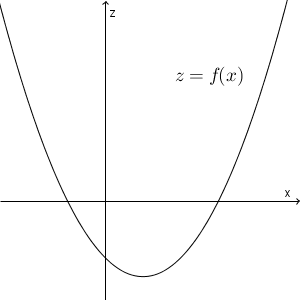
$f(x)=0$ の解は
\begin{eqnarray}
& &
\frac{3y^2-1 \pm \sqrt{(-3y^2+1)^2-4(1-y^2)y} }{2} \\[5pt]
&=&
\frac{3y^2-1 \pm \sqrt{9y^4 -6y^2 +1 -4y +4y^3} }{2} \\[5pt]
\end{eqnarray}なので、「(右辺)>(中辺)」が成り立つ範囲は\[ x \gt \frac{3y^2-1 + \sqrt{9y^4 +4y^3 -6y^2 -4y +1 } }{2} \]となる。
以上から、与えられた不等式が成り立つ x の範囲は\[ x \gt \frac{3y^2-1 + \sqrt{9y^4 +4y^3 -6y^2 -4y +1 } }{2} \]である。
解説
「左辺<中辺」はつねに成り立ちます。
「中辺<右辺」を示す箇所では、 $z=f(x)$ のグラフが原点を通る可能性がある点に注意です。 $y=1$ のときにグラフは原点を通りますが、この場合は、グラフと x 軸が2点で交わるとは限らないし、交点の x 座標の符号がどうなっているかも確定しません。
しかし、ここに「軸が z 軸より右にある」という条件が加われば、原点を通っているかどうかにかかわらず、 x 軸と2点で交わること、そして、その x 座標については、片方は正、片方は0以下であることが言えます。
解答編 つづき
問題
(2) 命題P を証明せよ。
解答
$x=10^{200}$, $\displaystyle y=\frac{10^{99}-1}{27}$ とする。
$10^{99}-1$ は、9が99個並ぶ99桁の整数であり、 $\displaystyle \frac{10^{99}-1}{9}$ は1が99個並ぶ99桁の整数である。各桁の和は3の倍数なので元の数も3で割れるため、 $\displaystyle y=\frac{10^{99}-1}{27}$ は整数である。
また、この x, y は次のようにして(1)で求めた条件が成り立つことがわかる。
\begin{eqnarray}
& &
\frac{3y^2-1 + \sqrt{9y^4 +4y^3 -6y^2 -4y +1 } }{2} \\[5pt]
&\lt&
\frac{3y^2-0 + \sqrt{9y^4 +4y^4 -0 -0 +y^4 } }{2} \\[5pt]
&=&
\frac{3y^2 + \sqrt{14} \ y^2 }{2} \\[5pt]
&\lt&
4y^2 \\[5pt]
&=&
4\left(\frac{10^{99}-1}{27}\right)^2 \\[5pt]
&\lt&
4\times \frac{10^{198} }{27^2} \\[5pt]
&\lt&
10^{200} \\[5pt]
&=&
x \\[5pt]
\end{eqnarray}よって、(1)の不等式が成り立つ。
\begin{eqnarray}
x^3+3yx^2
&=&
x^2(x+3y) \\
&=&
(x+3y) \times 10^{400} \\
\end{eqnarray}であり、
\begin{eqnarray}
x^3+(3y+1)x^2
&=&
x^2(x+3y+1) \\
&=&
(x+3y+1) \times 10^{400} \\
\end{eqnarray}である。ここで、 $3y$ は1が99個並ぶ99桁の整数であり、 $x=10^{200}$ であるから、 $x+3y$ は1番下の位から1が連続して99回現れる数字である。
$A=(x+y-1)(x+y)(x+y+1)$ とすると、これは連続する3つの自然数の積である。また、
\begin{eqnarray}
(x+3y) \times 10^{400} \lt A \lt (x+3y+1) \times 10^{400}
\end{eqnarray}を満たす。これより、 A を10進数で表したとき、1番下の位から数えて、401番目から499番目までのところで、連続して1が現れる。よって、命題P が示された。
解説
(1)の不等式と命題Pを見比べると、(1)の中辺が連続する3つの自然数の積に対応していることがわかります。なので、(1)を使い、うまい x, y を探してくることがカギとなります。
(1)の不等式の使い方は、例えば $111000 \lt X \lt 112000$ という条件下なら、 X の値が何であっても、先頭に1が3つ並びます。このように、「数字の右側はどうなっているかはわからないが、左の方で1が続く」ようにするために、(1)の不等式を使います。
そう考えると、 $3y$ は1が99個以上並ぶ数字とすればよく、 x は(1)の不等式が成り立つような、つまり、(1)の答えを満たすようなものをとってくればいいことがわかります。命題Pは、存在を示すだけでいいので、自分の都合のいい数字をとってくればOKです。上の解答で使った数字が唯一の解というわけではありません。
上の解答で用いた y を具体的に書くと、 $370370\cdots 37$ となります。また、 A を直接計算したものはここ(Wolfram|Alpha)にあります。Resultの「More digits」をクリックすれば、すべての数字を見ることができます。先頭に1があって、次に0が101個並んで、その次に1が99個並ぶ、601桁の数です。
ところで、この問題で何をやっていたかを、イメージで説明してみます。
(1)の冒頭で計算したように、 $x+y-1$, $x+y$, $x+y+1$ の積は\[ x^3+3x^2y+3xy^2+y^3-x-y \]となります。 $10^{200}$ のような、大きな10の累乗を x に入れると、この積は、左側が $x^3$ の影響を受け、右側は $3xy^2+y^3-x-y$ の影響を受け、その間の部分は $3x^2y$ の影響を受けます。 x が大きければ、この3か所は分断されます。そのため、この真ん中にあたる $3x^2y$ の部分では、自分の好きな3の倍数が出せるようにコントロールできる、ということだったんですね。
この問題では、「1が連続して99回現れる数」を作るために、 $x=10^{200}$ とし、 $3y$ を1が連続して99回並ぶ数にしました。しかし、「1が連続して99回」にはあまり意味はなくて、 x, y をうまく選べば、「2が連続して99回並ぶ数」となるようにすることもできるし、「1が999回並ぶ数」となるようにすることもできることがわかります。3の倍数なら、どんな数でも出せます。





