東京大学 文系 2019年度 第2問 解説
問題編
問題
O を原点とする座標平面において、点 $\mathrm{ A }(2,2)$ を通り、線分 OA と垂直な直線を $l$ とする。座標平面上を点 $\mathrm{ P }(p,q)$ が次の2つの条件をみたしながら動く。
条件1: $8\leqq \overrightarrow{ \mathrm{ OA } }\cdot \overrightarrow{ \mathrm{ OP } } \leqq 17$
条件2:点 O と直線 l の距離を c とし、点 $\mathrm{ P }(p,q)$ と直線 l の距離を d とするとき $cd\geqq (p-1)^2$
このとき、P が動く領域を D とする。さらに、x 軸の正の部分と線分 OP のなす角を $\theta$ とする。
(1) D を図示し、その面積を求めよ。
(2) $\cos\theta$ のとりうる値の範囲を求めよ。
考え方
めんどくさそうな条件に見えますが、一つ一つ言い換えていくと、それほどめんどうではありません。条件1から、直線で囲まれた領域を動くことがわかります。条件2は、点と直線の距離の公式を使うといいでしょう。条件1を使えば、絶対値を外すことができます。このことから、領域や面積を求めることができます。
(2)は、どのような場合に $\cos\theta$ が最大・最小になるかを、図を見ながら考えてみましょう。答えは不安な気持ちになる形です。
解答編
問題
O を原点とする座標平面において、点 $\mathrm{ A }(2,2)$ を通り、線分 OA と垂直な直線を $l$ とする。座標平面上を点 $\mathrm{ P }(p,q)$ が次の2つの条件をみたしながら動く。
条件1: $8\leqq \overrightarrow{ \mathrm{ OA } }\cdot \overrightarrow{ \mathrm{ OP } } \leqq 17$
条件2:点 O と直線 l の距離を c とし、点 $\mathrm{ P }(p,q)$ と直線 l の距離を d とするとき $cd\geqq (p-1)^2$
このとき、P が動く領域を D とする。さらに、x 軸の正の部分と線分 OP のなす角を $\theta$ とする。
(1) D を図示し、その面積を求めよ。
解答
条件1は
\begin{eqnarray}
& & 8 \leqq \overrightarrow{ \mathrm{ OA } }\cdot \overrightarrow{ \mathrm{ OP } } \leqq 17 \\[5pt]
& & 8 \leqq 2p+2q \leqq 17 \\[5pt]
& & 4 \leqq p+q \leqq \frac{17}{2} \\[5pt]
& & -p+4 \leqq q \leqq -p+\frac{17}{2} \\[5pt]
\end{eqnarray}と同値である。
線分 OA の傾きは $1$ なので、直線 $l$ の傾きは $-1$ となる。よって、点 $\mathrm{ A }(2,2)$ を通るので、直線 $l$ の方程式は\[ y=-x+4 \]である。点 O と直線 $l$ の距離は、線分 OA の長さと等しいので、 $c=2\sqrt{2}$ である。点 P と直線 $l$ との距離は、\[ \frac{|p+q-4|}{\sqrt{1^2+1^2} }=\frac{|p+q-4|}{\sqrt{2} } \]である。よって、条件2は
\begin{eqnarray}
cd & \geqq & (p-1)^2 \\[5pt]
2|p+q-4| & \geqq & (p-1)^2 \\[5pt]
\end{eqnarray}と同値である。
条件1のもとでは、 $p+q\geqq 4$ なので、条件1を満たしている場合は、条件2は次のように変形できる。
\begin{eqnarray}
2(p+q-4) & \geqq & (p-1)^2 \\[5pt]
2q & \geqq & p^2-2p+1-2p+8 \\[5pt]
q & \geqq & \frac{1}{2}p^2-2p+\frac{9}{2} \\[5pt]
\end{eqnarray}
ここで、 $-p+4=\dfrac{1}{2}p^2-2p+\dfrac{9}{2}$ とすると
\begin{eqnarray}
\frac{1}{2}p^2-p+\frac{1}{2} &=& 0 \\[5pt]
(p-1)^2 &=& 0 \\[5pt]
p &=& 1 \\[5pt]
\end{eqnarray}となる。
また、 $-p+\dfrac{17}{2}=\dfrac{1}{2}p^2-2p+\dfrac{9}{2}$ とすると
\begin{eqnarray}
\frac{1}{2}p^2-p-4 &=& 0 \\[5pt]
p^2-2p-8 &=& 0 \\[5pt]
(x-4)(x+2) &=& 0 \\[5pt]
p &=& -2,4 \\[5pt]
\end{eqnarray}となる。
以上から、領域 D は、下の図の色のついた部分(境界線上の点を含む)となる。
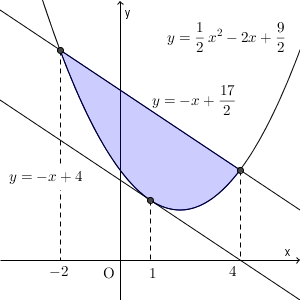
また、この領域の面積は
\begin{eqnarray}
& &
\int_{-2}^4 \left\{\left(-p+\dfrac{17}{2}\right)-\left(\dfrac{1}{2}p^2-2p+\frac{9}{2}\right)\right\} dp \\[5pt]
&=&
-\frac{1}{2}\int_{-2}^4 (p-4)(p+2) dp \\[5pt]
&=&
\frac{1}{2}\times\frac{\{(4-(-2))\}^3}{6} \\[5pt]
&=&
18
\end{eqnarray}となる。
((1)終)
解答編 つづき
問題
(2) $\cos\theta$ のとりうる値の範囲を求めよ。
解答
放物線 $y=\dfrac{1}{2}x^2-2x+\dfrac{9}{2}$ と直線 $y=mx$ が接する場合を考える。このとき
\begin{eqnarray}
\frac{1}{2}x^2-2x+\frac{9}{2} &=& mx \\[5pt]
x^2-2(m+2)x+9 &=& 0 \\[5pt]
\end{eqnarray}が重解を持つので、
\begin{eqnarray}
(m+2)^2-9 &=& 0 \\[5pt]
m+2 &=& \pm 3 \\[5pt]
m &=& 1,-5 \\[5pt]
\end{eqnarray}となる。このとき、重解は $m+2$ と表せるから、 $\pm 3$ である。領域 D の $x$ 座標は $-2$ 以上 $4$ 以下なので、領域 D は、 $y=x$ と接するが、 $y=-5x$ とは接しないことがわかる。
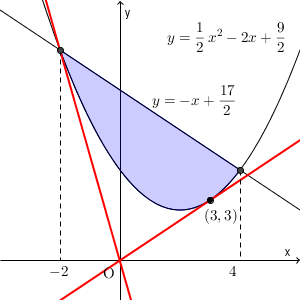
以上から、 $\theta$ を $0$ 以上 $\pi$ 以下とすると、 $\theta$ が最小となるのは、点 P が $(3,3)$ のときであり、このときの $\cos\theta$ は $\dfrac{1}{\sqrt{2} }$ である。
一方、 $\theta$ が最大となるのは P の $x$ 座標が $-2$ のときである。 P の $x$ 座標が $-2$ のとき、 $y$ 座標は $-(-2)+\dfrac{17}{2}=\dfrac{21}{2}$ だから、このときの $\cos\theta$ は
\begin{eqnarray}
& &
\frac{-2}{\sqrt{(-2)^2+\left(\frac{21}{2}\right)^2} } \\[5pt]
&=&
\frac{-2}{\sqrt{4+\frac{441}{4} }} \\[5pt]
&=&
-\frac{4}{\sqrt{457} } \\[5pt]
\end{eqnarray}である。
$\cos\theta$ はこの間の値をすべてとるので、とりうる値の範囲は\[ -\dfrac{4}{\sqrt{457} } \leqq \cos\theta \leqq \frac{1}{\sqrt{2} } \]となる。
((2)終)





