東京大学 文系 2017年度 第1問 解説
問題編
問題
座標平面において2つの放物線 $A: y=s(x-1)^2$ と $B:y=-x^2+t^2$ を考える。ただし、 s, t は実数で、 $0\lt s$, $0\lt t \lt 1$ をみたすとする。放物線 A と x 軸および y 軸で囲まれる領域の面積を P とし、放物線 B の $x\geqq 0$ の部分と x 軸および y 軸で囲まれる領域の面積を Q とする。 A と B がただ1点を共有するとき、 $\dfrac{Q}{P}$ の最大値を求めよ。
考え方
P, Q は s, t を使って具体的に計算できます。また、共有点が1点という条件から s, t に関する条件も導けます。これらを用いて $\dfrac{Q}{P}$ を1つの文字で表すことができます。あとは、この増減表をかけば、最大値が求められます。
解答編
問題
座標平面において2つの放物線 $A: y=s(x-1)^2$ と $B:y=-x^2+t^2$ を考える。ただし、 s, t は実数で、 $0\lt s$, $0\lt t \lt 1$ をみたすとする。放物線 A と x 軸および y 軸で囲まれる領域の面積を P とし、放物線 B の $x\geqq 0$ の部分と x 軸および y 軸で囲まれる領域の面積を Q とする。 A と B がただ1点を共有するとき、 $\dfrac{Q}{P}$ の最大値を求めよ。
解答
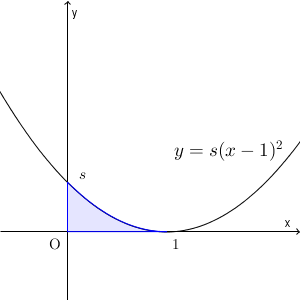
\begin{eqnarray} P &=& \int_0^1 s(x-1)^2 dx \\[5pt] &=& \int_0^1 s(x^2-2x+1) dx \\[5pt] &=& s\left[ \frac{1}{3}x^3-x^2+x \right]_0^1 \\[5pt] &=& \frac{1}{3}s \end{eqnarray}となる。
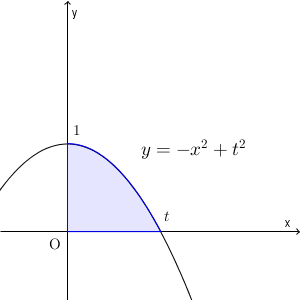
\begin{eqnarray}
Q
&=&
\int_0^t (-x^2+t^2) dx \\[5pt]
&=&
\left[ -\frac{1}{3}x^3 +t^2x \right]_0^t \\[5pt]
&=&
-\frac{1}{3}t^3 +t^3 \\[5pt]
&=&
\frac{2}{3}t^3 \\[5pt]
\end{eqnarray}となる。
また、2つの放物線 A, B の共有点が1点なので、次の方程式
\begin{eqnarray}
s(x-1)^2 &=& -x^2+t^2 \\
(s+1)x^2 -2sx +s-t^2 &=& 0
\end{eqnarray}は重解を持つ。よって、判別式は0となるので
\begin{eqnarray}
(-2s)^2-4(s+1)(s-t^2) &=& 0 \\
s^2-(s^2-st^2+s-t^2) &=& 0 \\
st^2 -s +t^2 &=& 0 \\
s(t^2-1) &=& -t^2 \\
\end{eqnarray}ここで、 $0\lt t \lt 1$ より $t^2-1\ne 0$ なので
\begin{eqnarray}
s &=& \frac{t^2}{1-t^2}
\end{eqnarray}が成り立つ。 $0\lt t \lt 1$ の範囲で、右辺は正なので $s\gt 0$ はつねに成り立つ。
このとき、
\begin{eqnarray}
\frac{Q}{P}
&=&
\frac{2}{3}t^3 \div \frac{1}{3}s \\[5pt]
&=&
2t^3 \times \frac{1-t^2}{t^2} \\[5pt]
&=&
2t(1-t^2) \\[5pt]
&=&
2t-2t^3 \\[5pt]
\end{eqnarray}となる。この式を $f(t)$ とおく。
\begin{eqnarray}
f'(t)
&=&
2-6t^2
\end{eqnarray}なので、 $f'(t)=0$ とすると $t=\pm\dfrac{\sqrt{3} }{3}$ である。よって、 $0\lt t \lt 1$ の範囲で $f(t)$ の増減表は次のようになる。
\begin{array}{c|ccccc}
t & 0 & \cdots & \dfrac{\sqrt{3} }{3} & \cdots & 1 \\
\hline
f' & & + & 0 & - & \\
\hline
f & & \nearrow & & \searrow &
\end{array}ここで、
\begin{eqnarray}
f\left(\frac{\sqrt{3} }{3}\right)
&=&
2\cdot \frac{\sqrt{3} }{3} -2 \left(\frac{\sqrt{3} }{3}\right)^3 \\[5pt]
&=&
\frac{2\sqrt{3} }{3} -\frac{2\sqrt{3} }{9} \\[5pt]
&=&
\frac{4\sqrt{3} }{9} \\[5pt]
\end{eqnarray}なので、増減表とこの結果から、求める最大値は $\dfrac{4\sqrt{3} }{9}$ となる。
(終)
解説
P, Q は、積分すれば s, t を使った式で書くことができます。2つの放物線の共有点が1点だけであることから、「判別式が0になる」という条件を使って、 s, t の間に成り立つ関係式を作っています。 s について見ると一次式なので、 s を消すように変形しましょう。
これらから $\dfrac{Q}{P}$ は t を用いた関数で表現できます。微分して増減表をかけば、最大値をどこでとるかがわかり、その値も具体的に計算して求めることができます。





