東京都 公立高校 2018年度 第1問 解説
問題編
問題
(サイトレイアウトの都合のため、「右の表」「右の図」は「下の表」「下の図」と読み替えて考えてください)
[問1] $5-\dfrac{1}{3}\times(-9)$ を計算せよ。
[問2] $8(a+b)-(4a-b)$ を計算せよ。
[問3] $(\sqrt{7}+2\sqrt{3})(\sqrt{7}-2\sqrt{3})$ を計算せよ。
[問4] 一次方程式 $4x-5=x-6$ を解け。
[問5] 連立方程式 \begin{eqnarray} \left\{ \begin{array}{l} 7x -y =8 \\ -9x +4y =6 \end{array} \right. \end{eqnarray} を解け。[問6] 二次方程式 $x^2+12x+35=0$ を解け。
[問7] 次の $\bbox[2px, border:1px solid]{\qquad \sf{ } }$ の中の「あ」「い」に当てはまる数字をそれぞれ答えよ。
右の表は、東京のある地点における4月7日の最高気温について、過去40年間の記録を調査し、度数分布表に整理したものである。
最高気温が18℃以上であった日数は、全体の日数の $\myBox{あい}$ %である。
階級(℃) 度数(日) 以上 未満 8 ~ 10 1 10 ~ 12 4 12 ~ 14 2 14 ~ 16 7 16 ~ 18 8 18 ~ 20 5 20 ~ 22 9 22 ~ 24 4 計 40 [問8] 次の $\bbox[2px, border:1px solid]{\qquad \sf{ } }$ の中の「う」「え」「お」に当てはまる数字をそれぞれ答えよ。
右の図1で、 $\ell /\!/ m$ のとき、 x で示した角の大きさは、 $\myBox{うえお}$ 度である。
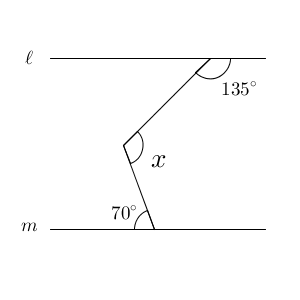
図1 [問9] 右の図2のように、円O の周上に点P、円O の内部に点Q がある。
点P が点Q に重なるように1回だけ折るとき、折り目と重なる直線 $\ell$ を、定規とコンパスを用いて作図し、直線 $\ell$ を示す文字 $\ell$ も書け。
ただし、作図に用いた線は消さないでおくこと。
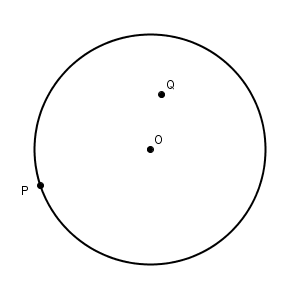
図2
考え方
どれも標準的な問題です。問2は、符号に気をつけましょう。問6は、解の公式を使う必要はありません。
問8は補助線をひいて考えましょう。問9は、直線 $\ell$ と PQ との関係について考えると、何を作図すればいいかひらめくと思います。
解答編
問題
(サイトレイアウトの都合のため、「右の表」「右の図」は「下の表」「下の図」と読み替えて考えてください)
[問1] $5-\dfrac{1}{3}\times(-9)$ を計算せよ。
[問2] $8(a+b)-(4a-b)$ を計算せよ。
[問3] $(\sqrt{7}+2\sqrt{3})(\sqrt{7}-2\sqrt{3})$ を計算せよ。
解説
まずは、計算問題です。
問1は、右の掛け算の方から計算します。
\begin{eqnarray}
5-\dfrac{1}{3}\times(-9)
&=&
5+3 \\[5pt]
&=&
8
\end{eqnarray}これが答えです。
問2は、カッコをはずして計算していきます。2つ目のカッコをはずすときの b の符号に気をつけましょう。
\begin{eqnarray}
& &
8(a+b)-(4a-b) \\[5pt]
&=&
8a+8b-4a+b \\[5pt]
&=&
4a+9b \\[5pt]
\end{eqnarray}これが答えです。
問3は、和と差の積なので、展開の公式を使いましょう。
\begin{eqnarray}
& &
(\sqrt{7}+2\sqrt{3})(\sqrt{7}-2\sqrt{3}) \\[5pt]
&=&
(\sqrt{7})^2-(2\sqrt{3})^2 \\[5pt]
&=&
7-4\times 3 \\[5pt]
&=&
7-12 \\[5pt]
&=&
-5
\end{eqnarray}これが答えです。
解答
問1: $8$
問2: $4a+9b$
問3: $-5$
(各問5点)
解答編 つづき
問題
[問4] 一次方程式 $4x-5=x-6$ を解け。
[問5] 連立方程式 \begin{eqnarray} \left\{ \begin{array}{l} 7x -y =8 \\ -9x +4y =6 \end{array} \right. \end{eqnarray} を解け。[問6] 二次方程式 $x^2+12x+35=0$ を解け。
解説
次の3問は方程式です。
問4は、次のようにして解きます。
\begin{eqnarray}
4x-5 &=& x-6 \\[5pt]
4x-x &=& 5-6 \\[5pt]
3x &=& -1 \\[5pt]
x &=& -\frac{1}{3} \\[5pt]
\end{eqnarray}これが答えです。
問5は、次の連立方程式ですね。
\begin{eqnarray}
\left\{
\begin{array}{l}
7x -y =8 \\
-9x +4y =6
\end{array}
\right.
\end{eqnarray}1つ目の式を4倍したものと、2つ目の式を並べてみます。
\begin{eqnarray}
28x -4y =32 \\
-9x +4y =6
\end{eqnarray}左辺同士、右辺同士を足すと、 y が消えて、次のようになります。
\begin{eqnarray}
28x-9x &=& 32+6 \\[5pt]
19x &=& 38 \\[5pt]
x &=& 2 \\[5pt]
\end{eqnarray}これを1つ目の式に代入して
\begin{eqnarray}
7\times 2-y&=&8 \\[5pt]
-y&=&8-14 \\[5pt]
-y&=&-6 \\[5pt]
y&=&6 \\[5pt]
\end{eqnarray}と求められます。
問6は、因数分解ができるので、因数分解をして解きましょう。
\begin{eqnarray}
x^2+12x+35 &=& 0 \\[5pt]
(x+5)(x+7) &=& 0 \\[5pt]
x&=&-5,-7
\end{eqnarray}これが答えです。
解答
問4: $x=-\dfrac{1}{3}$
問5: $x=2,\ y=6$
問6: $x=-5,-7$
(各問5点)
解答編 つづき
問題
[問7] 次の $\bbox[2px, border:1px solid]{\qquad \sf{ } }$ の中の「あ」「い」に当てはまる数字をそれぞれ答えよ。
右の表は、東京のある地点における4月7日の最高気温について、過去40年間の記録を調査し、度数分布表に整理したものである。
最高気温が18℃以上であった日数は、全体の日数の $\myBox{あい}$ %である。
階級(℃) 度数(日) 以上 未満 8 ~ 10 1 10 ~ 12 4 12 ~ 14 2 14 ~ 16 7 16 ~ 18 8 18 ~ 20 5 20 ~ 22 9 22 ~ 24 4 計 40
解説
まず、最高気温が18℃以上の日数を計算しましょう。18℃以上20℃未満、20℃以上22℃未満、22℃以上24℃未満、この3つの日数を足せばいいですね。これを計算すると\[ 5+9+4=18 \]なので、18日だ、とわかります。
これが全体の何%であるかは、割ればわかりますね。\[ 18\div 40=0.45 \]なので、45%と求められます。
解答
あ: 4
い: 5
(完答で5点)
解答編 つづき
問題
[問8] 次の $\bbox[2px, border:1px solid]{\qquad \sf{ } }$ の中の「う」「え」「お」に当てはまる数字をそれぞれ答えよ。
右の図1で、 $\ell /\!/ m$ のとき、 x で示した角の大きさは、 $\myBox{うえお}$ 度である。

図1
解説
図のように、 $\ell, m$ に平行な線をひき、 x を分割して考えましょう。

x の下側の部分は、錯角を考えて、70度とわかります。上側の部分も、錯角を考えて、\[
180-135=45 \]から、45度だとわかります。この2つを足せば x の大きさになるので、\[
70+45=115 \]だから、115度が答えだとわかります。
解答
う: 1
え: 1
お: 5
(完答で5点)
解答編 つづき
問題
[問9] 右の図2のように、円O の周上に点P、円O の内部に点Q がある。
点P が点Q に重なるように1回だけ折るとき、折り目と重なる直線 $\ell$ を、定規とコンパスを用いて作図し、直線 $\ell$ を示す文字 $\ell$ も書け。
ただし、作図に用いた線は消さないでおくこと。

図2
解説
P と Q が重なるように折るため、折り目は線対称の軸となります。これは、線分 PQ の垂直二等分線をかけばいいですね。
解答
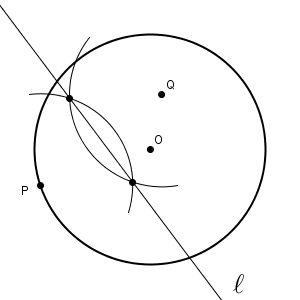
(6点)





