共通テスト数学II・数学B 2021年度第5問解説

🕒 2021/01/18 🔄 2023/05/01

【第3問～第5問から2問選択】

問題編

問題

　1辺の長さが $1$ の正五角形の対角線の長さを $a$ とする。

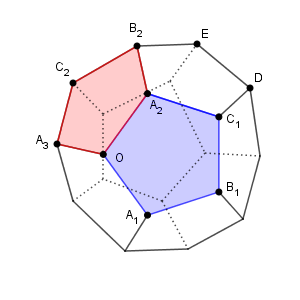
(1) 1辺の長さが $1$ の正五角形 $\mathrm{ OA_1B_1C_1A_2 }$ を考える。

　$\angle \mathrm{ A_1C_1B_1 }=\myBox{アイ}^{\circ}$, $\angle \mathrm{ C_1A_1A_2 }=\mybox{アイ}^{\circ}$ となることから、 $\overrightarrow{ \mathrm{ A_1A_2 } }$ と $\overrightarrow{ \mathrm{ B_1C_1 } }$ は平行である。ゆえに\[ \overrightarrow{ \mathrm{ A_1A_2 } }=\myBox{ウ}\overrightarrow{ \mathrm{ B_1C_1 } } \]であるから\[ \overrightarrow{ \mathrm{ B_1C_1 } }=\dfrac{1}{\mybox{ウ} }\overrightarrow{ \mathrm{ A_1A_2 } }=\frac{1}{\mybox{ウ} } \left(\overrightarrow{ \mathrm{ OA_2 } }-\overrightarrow{ \mathrm{ OA_1 } }\right) \]

　また、 $\overrightarrow{ \mathrm{ OA_1 } }$ と $\overrightarrow{ \mathrm{ A_2B_1 } }$ は平行で、さらに、 $\overrightarrow{ \mathrm{ OA_2 } }$ と $\overrightarrow{ \mathrm{ A_1C_1 } }$ も平行であることから
\begin{eqnarray} \overrightarrow{ \mathrm{ B_1C_1 } } &=& \overrightarrow{ \mathrm{ B_1A_2 } }+\overrightarrow{ \mathrm{ A_2O } }+\overrightarrow{ \mathrm{ OA_1 } }+\overrightarrow{ \mathrm{ A_1C_1 } } \\[5pt] &=& -\mybox{ウ}\overrightarrow{ \mathrm{ OA_1 } }-\overrightarrow{ \mathrm{ OA_2 } }+\overrightarrow{ \mathrm{ OA_1 } }+\mybox{ウ}\overrightarrow{ \mathrm{ OA_2 } } \\[5pt] &=& \left(\myBox{エ}-\myBox{オ}\right)\left(\overrightarrow{ \mathrm{ OA_2 } }-\overrightarrow{ \mathrm{ OA_1 } }\right) \end{eqnarray}となる。したがって\[ \frac{1}{\mybox{ウ} }=\mybox{エ}-\mybox{オ} \]が成り立つ。 $a\gt 0$ に注意してこれを解くと、 $a=\dfrac{1+\sqrt{5} }{2}$ を得る。
(2) 下の図のような、1辺の長さが $1$ の正十二面体を考える。正十二面体とは、どの面もすべて合同な正五角形であり、どの頂点にも三つの面が集まっているへこみのない多面体のことである。

　面 $\mathrm{ OA_1B_1C_1A_2 }$ に着目する。 $\overrightarrow{ \mathrm{ OA_1 } }$ と $\overrightarrow{ \mathrm{ A_2B_1 } }$ が平行であることから\[ \overrightarrow{ \mathrm{ OB_1 } }=\overrightarrow{ \mathrm{ OA_2 } }+\overrightarrow{ \mathrm{ A_2B_1 } } =\overrightarrow{ \mathrm{ OA_2 } }+\mybox{ウ}\overrightarrow{ \mathrm{ OA_1 } } \]である。また\[ \left|\overrightarrow{ \mathrm{ OA_2 } }-\overrightarrow{ \mathrm{ OA_1 } }\right|^2=\left|\overrightarrow{ \mathrm{ A_1A_2 } }\right|^2=\frac{\myBox{カ}+\sqrt{\myBox{キ} }}{\myBox{ク} } \]に注意すると\[ \overrightarrow{ \mathrm{ OA_1 } }\cdot \overrightarrow{ \mathrm{ OA_2 } }=\frac{\myBox{ケ}-\sqrt{\myBox{コ} }}{\myBox{サ} } \]を得る。

　ただし、 $\mybox{カ}$ ～ $\mybox{サ}$ は、文字 $a$ を用いない形で答えること。

　次に、面 $\mathrm{ OA_2B_2C_2A_3 }$ に着目すると\[ \overrightarrow{ \mathrm{ OB_2 } }=\overrightarrow{ \mathrm{ OA_3 } }+\mybox{ウ}\overrightarrow{ \mathrm{ OA_2 } } \]である。さらに\[ \overrightarrow{ \mathrm{ OA_2 } }\cdot \overrightarrow{ \mathrm{ OA_3 } } = \overrightarrow{ \mathrm{ OA_3 } }\cdot \overrightarrow{ \mathrm{ OA_1 } } =\frac{\mybox{ケ}-\sqrt{\mybox{コ} }}{\mybox{サ} } \]が成り立つことがわかる。ゆえに
\begin{eqnarray} \overrightarrow{ \mathrm{ OA_1 } }\cdot \overrightarrow{ \mathrm{ OB_2 } }=\myBox{シ} \\[5pt] \overrightarrow{ \mathrm{ OB_1 } }\cdot \overrightarrow{ \mathrm{ OB_2 } }=\myBox{ス} \\[5pt] \end{eqnarray}である。
$\mybox{シ}, \mybox{ス}$ の解答群（同じものを繰り返し選んでもよい。）

　0: $0$

　1: $1$

　2: $-1$

　3: $\dfrac{1+\sqrt{5} }{2}$

　4: $\dfrac{1-\sqrt{5} }{2}$

　5: $\dfrac{-1+\sqrt{5} }{2}$

　6: $\dfrac{-1-\sqrt{5} }{2}$

　7: $-\dfrac{1}{2}$

　8: $\dfrac{-1+\sqrt{5} }{4}$

　9: $\dfrac{-1-\sqrt{5} }{4}$

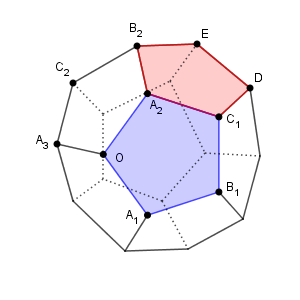
　最後に、面 $\mathrm{ A_2C_1DEB_2 }$ に着目する。\[ \overrightarrow{ \mathrm{ B_2D } }=\mybox{ウ} \overrightarrow{ \mathrm{ A_2C_1 } } =\overrightarrow{ \mathrm{ OB_1 } } \]であることに注意すると、4点 $\mathrm{ O, B_1, D, B_2 }$ は同一平面上にあり、四角形 $\mathrm{ OB_1DB_2 }$ は $\myBox{セ}$ ことがわかる。

$\mybox{セ}$ の解答群

　0: 正方形である
　1: 正方形ではないが、長方形である
　2: 正方形ではないが、ひし形である
　3: 長方形でもひし形でもないが、平行四辺形である
　4: 平行四辺形ではないが、台形である
　5: 台形でない

ただし、少なくとも一組の対辺が平行な四角形を台形という。

考え方

正十二面体が出てきて、かなりやっかいな見た目をしています。しかし、誘導が親切なので見た目ほど怖くはありません。 $a$ の値も書いてくれているし、計算結果もところどころ書いてくれているので、やさしさが感じられます。

最後の設問も、ベクトルを使わなくてもある程度は絞れます。図形からわかることも利用して解いていきましょう。

解答編

問題

　1辺の長さが $1$ の正五角形の対角線の長さを $a$ とする。

(1) 1辺の長さが $1$ の正五角形 $\mathrm{ OA_1B_1C_1A_2 }$ を考える。

　$\angle \mathrm{ A_1C_1B_1 }=\myBox{アイ}^{\circ}$, $\angle \mathrm{ C_1A_1A_2 }=\mybox{アイ}^{\circ}$ となることから、 $\overrightarrow{ \mathrm{ A_1A_2 } }$ と $\overrightarrow{ \mathrm{ B_1C_1 } }$ は平行である。ゆえに\[ \overrightarrow{ \mathrm{ A_1A_2 } }=\myBox{ウ}\overrightarrow{ \mathrm{ B_1C_1 } } \]であるから\[ \overrightarrow{ \mathrm{ B_1C_1 } }=\dfrac{1}{\mybox{ウ} }\overrightarrow{ \mathrm{ A_1A_2 } }=\frac{1}{\mybox{ウ} } \left(\overrightarrow{ \mathrm{ OA_2 } }-\overrightarrow{ \mathrm{ OA_1 } }\right) \]

解説

正五角形の内角の和は、 $180^{\circ}\times 3 = 540^{\circ}$ なので、 $\angle \mathrm{ A_1B_1C_1 }=108^{\circ}$ です。三角形 $\mathrm{ A_1B_1C_1 }$ は二等辺三角形なので、\[ \angle \mathrm{ A_1C_1B_1 }=36^{\circ} \]です。 $\angle \mathrm{ OA_1A_2 }$ も $\angle \mathrm{ B_1A_1C_1 }$ も同じように $36^{\circ}$ とわかるので、 $\angle \mathrm{ C_1A_1A_2 }=36^{\circ}$ だから、問題文にある通り、 $\overrightarrow{ \mathrm{ A_1A_2 } }$ と $\overrightarrow{ \mathrm{ B_1C_1 } }$ は平行だとわかります。また、向きが同じで大きさの比は $a:1$ だから\[ \overrightarrow{ \mathrm{ A_1A_2 } }=a\overrightarrow{ \mathrm{ B_1C_1 } } \]と書けます。

解答

アイ：36
ウ：a

解答編つづき

　また、 $\overrightarrow{ \mathrm{ OA_1 } }$ と $\overrightarrow{ \mathrm{ A_2B_1 } }$ は平行で、さらに、 $\overrightarrow{ \mathrm{ OA_2 } }$ と $\overrightarrow{ \mathrm{ A_1C_1 } }$ も平行であることから
\begin{eqnarray} \overrightarrow{ \mathrm{ B_1C_1 } } &=& \overrightarrow{ \mathrm{ B_1A_2 } }+\overrightarrow{ \mathrm{ A_2O } }+\overrightarrow{ \mathrm{ OA_1 } }+\overrightarrow{ \mathrm{ A_1C_1 } } \\[5pt] &=& -\mybox{ウ}\overrightarrow{ \mathrm{ OA_1 } }-\overrightarrow{ \mathrm{ OA_2 } }+\overrightarrow{ \mathrm{ OA_1 } }+\mybox{ウ}\overrightarrow{ \mathrm{ OA_2 } } \\[5pt] &=& \left(\myBox{エ}-\myBox{オ}\right)\left(\overrightarrow{ \mathrm{ OA_2 } }-\overrightarrow{ \mathrm{ OA_1 } }\right) \end{eqnarray}となる。したがって\[ \frac{1}{\mybox{ウ} }=\mybox{エ}-\mybox{オ} \]が成り立つ。 $a\gt 0$ に注意してこれを解くと、 $a=\dfrac{1+\sqrt{5} }{2}$ を得る。

解説

先ほどの話を回転して考えれば、\[ \overrightarrow{ \mathrm{ A_2B_1 } }=a\overrightarrow{ \mathrm{ OA_1 } },\ \overrightarrow{ \mathrm{ A_1C_1 } }=a\overrightarrow{ \mathrm{ OA_2 } } \]となることがわかります。こうして
\begin{eqnarray} \overrightarrow{ \mathrm{ B_1C_1 } } &=& \overrightarrow{ \mathrm{ B_1A_2 } }+\overrightarrow{ \mathrm{ A_2O } }+\overrightarrow{ \mathrm{ OA_1 } }+\overrightarrow{ \mathrm{ A_1C_1 } } \\[5pt] &=& -a\overrightarrow{ \mathrm{ OA_1 } }-\overrightarrow{ \mathrm{ OA_2 } }+\overrightarrow{ \mathrm{ OA_1 } }+a\overrightarrow{ \mathrm{ OA_2 } } \\[5pt] &=& (a-1)\left(\overrightarrow{ \mathrm{ OA_2 } }-\overrightarrow{ \mathrm{ OA_1 } }\right) \end{eqnarray}となることがわかります。

こうして、 $\overrightarrow{ \mathrm{ B_1C_1 } }$ は $\dfrac{1}{a}\left(\overrightarrow{ \mathrm{ OA_2 } }-\overrightarrow{ \mathrm{ OA_1 } }\right)$ とも $(a-1)\left(\overrightarrow{ \mathrm{ OA_2 } }-\overrightarrow{ \mathrm{ OA_1 } }\right)$ とも表せるので、\[ \frac{1}{a}=a-1 \]が成り立ちます。これを解けば
\begin{eqnarray} \frac{1}{a} &=& a-1 \\[5pt] a^2-a-1 &=& 0 \\[5pt] a &=& \frac{1\pm\sqrt{5} }{2} \end{eqnarray}となり、 $a\gt 0$ なので、問題文にある通り、 $a=\dfrac{1+\sqrt{5} }{2}$ と求められます。

解答

エオ：a1

解答編つづき

(2) 下の図のような、1辺の長さが $1$ の正十二面体を考える。正十二面体とは、どの面もすべて合同な正五角形であり、どの頂点にも三つの面が集まっているへこみのない多面体のことである。

　面 $\mathrm{ OA_1B_1C_1A_2 }$ に着目する。 $\overrightarrow{ \mathrm{ OA_1 } }$ と $\overrightarrow{ \mathrm{ A_2B_1 } }$ が平行であることから\[ \overrightarrow{ \mathrm{ OB_1 } }=\overrightarrow{ \mathrm{ OA_2 } }+\overrightarrow{ \mathrm{ A_2B_1 } } =\overrightarrow{ \mathrm{ OA_2 } }+\mybox{ウ}\overrightarrow{ \mathrm{ OA_1 } } \]である。また\[ \left|\overrightarrow{ \mathrm{ OA_2 } }-\overrightarrow{ \mathrm{ OA_1 } }\right|^2=\left|\overrightarrow{ \mathrm{ A_1A_2 } }\right|^2=\frac{\myBox{カ}+\sqrt{\myBox{キ} }}{\myBox{ク} } \]に注意すると\[ \overrightarrow{ \mathrm{ OA_1 } }\cdot \overrightarrow{ \mathrm{ OA_2 } }=\frac{\myBox{ケ}-\sqrt{\myBox{コ} }}{\myBox{サ} } \]を得る。

　ただし、 $\mybox{カ}$ ～ $\mybox{サ}$ は、文字 $a$ を用いない形で答えること。

解説

先ほど見たように、 $\overrightarrow{ \mathrm{ A_2B_1 } }=a\overrightarrow{ \mathrm{ OA_1 } }$ とかけることから、問題文にある通り
\begin{eqnarray} \overrightarrow{ \mathrm{ OB_1 } } &=& \overrightarrow{ \mathrm{ OA_2 } }+\overrightarrow{ \mathrm{ A_2B_1 } } \\[5pt] &=& \overrightarrow{ \mathrm{ OA_2 } }+a\overrightarrow{ \mathrm{ OA_1 } } \\[5pt] \end{eqnarray}が成り立ちます。

また、 $\mathrm{ A_1A_2 }$ の長さは $a=\dfrac{1+\sqrt{5} }{2}$ なので
\begin{eqnarray} \left|\overrightarrow{ \mathrm{ OA_2 } }-\overrightarrow{ \mathrm{ OA_1 } }\right|^2 &=& \left|\overrightarrow{ \mathrm{ A_1A_2 } }\right|^2 =a^2 \\[5pt] &=& \frac{1+2\sqrt{5}+5}{4}=\frac{3+\sqrt{5} }{2} \end{eqnarray}となります。（ $a^2-a-1=0$ なので $a^2=a+1$ と求めてもいいです。）

ここで、 $\left|\overrightarrow{ \mathrm{ OA_2 } }-\overrightarrow{ \mathrm{ OA_1 } }\right|^2$ は
\begin{eqnarray} & & \left|\overrightarrow{ \mathrm{ OA_2 } }\right|^2-2\overrightarrow{ \mathrm{ OA_2 } }\cdot\overrightarrow{ \mathrm{ OA_1 } }+\left|\overrightarrow{ \mathrm{ OA_1 } }\right|^2 \\[5pt] &=& 1-2\overrightarrow{ \mathrm{ OA_2 } }\cdot\overrightarrow{ \mathrm{ OA_1 } }+1 \\[5pt] &=& 2-2\overrightarrow{ \mathrm{ OA_2 } }\cdot\overrightarrow{ \mathrm{ OA_1 } } \\[5pt] \end{eqnarray}とも表せるので、 \begin{eqnarray} 2-2\overrightarrow{ \mathrm{ OA_2 } }\cdot\overrightarrow{ \mathrm{ OA_1 } } &=& \frac{3+\sqrt{5} }{2} \\[5pt] -2\overrightarrow{ \mathrm{ OA_2 } }\cdot\overrightarrow{ \mathrm{ OA_1 } } &=&\frac{-1+\sqrt{5} }{2} \\[5pt] \overrightarrow{ \mathrm{ OA_1 } }\cdot\overrightarrow{ \mathrm{ OA_2 } } &=&\frac{1-\sqrt{5} }{4} \\[5pt] \end{eqnarray}と求められます。

解答

カキク：352
ケコサ：154

解答編つづき

　次に、面 $\mathrm{ OA_2B_2C_2A_3 }$ に着目すると\[ \overrightarrow{ \mathrm{ OB_2 } }=\overrightarrow{ \mathrm{ OA_3 } }+\mybox{ウ}\overrightarrow{ \mathrm{ OA_2 } } \]である。さらに\[ \overrightarrow{ \mathrm{ OA_2 } }\cdot \overrightarrow{ \mathrm{ OA_3 } } = \overrightarrow{ \mathrm{ OA_3 } }\cdot \overrightarrow{ \mathrm{ OA_1 } } =\frac{\mybox{ケ}-\sqrt{\mybox{コ} }}{\mybox{サ} } \]が成り立つことがわかる。ゆえに
\begin{eqnarray} \overrightarrow{ \mathrm{ OA_1 } }\cdot \overrightarrow{ \mathrm{ OB_2 } }=\myBox{シ} \\[5pt] \overrightarrow{ \mathrm{ OB_1 } }\cdot \overrightarrow{ \mathrm{ OB_2 } }=\myBox{ス} \\[5pt] \end{eqnarray}である。
$\mybox{シ}, \mybox{ス}$ の解答群（同じものを繰り返し選んでもよい。）

　0: $0$

　1: $1$

　2: $-1$

　3: $\dfrac{1+\sqrt{5} }{2}$

　4: $\dfrac{1-\sqrt{5} }{2}$

　5: $\dfrac{-1+\sqrt{5} }{2}$

　6: $\dfrac{-1-\sqrt{5} }{2}$

　7: $-\dfrac{1}{2}$

　8: $\dfrac{-1+\sqrt{5} }{4}$

　9: $\dfrac{-1-\sqrt{5} }{4}$

解説

面 $\mathrm{ OA_2B_2C_2A_3 }$ についても、面 $\mathrm{ OA_1B_1C_1A_2 }$ のときと同じように考えれば、 $\mathrm{ A_3B_2 }$ は $\mathrm{ OA_2 }$ に平行で長さが $a$ なので
\begin{eqnarray} \overrightarrow{ \mathrm{ OB_2 } } &=& \overrightarrow{ \mathrm{ OA_3 } } + \overrightarrow{ \mathrm{ A_3B_2 } } \\[5pt] &=& \overrightarrow{ \mathrm{ OA_3 } } + a\overrightarrow{ \mathrm{ OA_2 } } \\[5pt] \end{eqnarray}と書けます。

また、 $\overrightarrow{ \mathrm{ OA_1 } }\cdot \overrightarrow{ \mathrm{ OA_2 } }$ も $\overrightarrow{ \mathrm{ OA_2 } }\cdot \overrightarrow{ \mathrm{ OA_3 } }$ も $\overrightarrow{ \mathrm{ OA_3 } }\cdot \overrightarrow{ \mathrm{ OA_1 } }$ も $1\cdot 1\cdot \cos 108^{\circ}$ と表せるので、すべて同じ値です。なので、問題文にある通り、\[ \overrightarrow{ \mathrm{ OA_2 } }\cdot \overrightarrow{ \mathrm{ OA_3 } } = \overrightarrow{ \mathrm{ OA_3 } }\cdot \overrightarrow{ \mathrm{ OA_1 } } =\frac{1-\sqrt{5} }{4} \]が成り立つことがわかります

こうして、
\begin{eqnarray} & & \overrightarrow{ \mathrm{ OA_1 } }\cdot \overrightarrow{ \mathrm{ OB_2 } } \\[5pt] &=& \overrightarrow{ \mathrm{ OA_1 } }\cdot \left(\overrightarrow{ \mathrm{ OA_3 } }+a\overrightarrow{ \mathrm{ OA_2 } }\right) \\[5pt] &=& \overrightarrow{ \mathrm{ OA_1 } }\cdot\overrightarrow{ \mathrm{ OA_3 } } +a\overrightarrow{ \mathrm{ OA_1 } }\cdot\overrightarrow{ \mathrm{ OA_2 } } \\[5pt] &=& \frac{1-\sqrt{5} }{4} +\frac{1+\sqrt{5} }{2}\cdot \frac{1-\sqrt{5} }{4} \\[5pt] &=& \frac{1-\sqrt{5} }{4} +\frac{1-5}{8} \\[5pt] &=& \frac{-1-\sqrt{5} }{4} \end{eqnarray}と求められます。

また、(2)の冒頭で $\overrightarrow{ \mathrm{ OB_1 } }=\overrightarrow{ \mathrm{ OA_2 } }+a\overrightarrow{ \mathrm{ OA_1 } }$ と求めていたので、
\begin{eqnarray} & & \overrightarrow{ \mathrm{ OB_1 } }\cdot \overrightarrow{ \mathrm{ OB_2 } } \\[5pt] &=& \left(\overrightarrow{ \mathrm{ OA_2 } }+a\overrightarrow{ \mathrm{ OA_1 } }\right)\cdot \left(\overrightarrow{ \mathrm{ OA_3 } }+a\overrightarrow{ \mathrm{ OA_2 } }\right) \\[5pt] &=& \overrightarrow{ \mathrm{ OA_2 } } \cdot \overrightarrow{ \mathrm{ OA_3 } } +a \overrightarrow{ \mathrm{ OA_2 } } \cdot \overrightarrow{ \mathrm{ OA_2 } } +a \overrightarrow{ \mathrm{ OA_1 } } \cdot \overrightarrow{ \mathrm{ OA_3 } } +a^2\overrightarrow{ \mathrm{ OA_1 } } \cdot \overrightarrow{ \mathrm{ OA_2 } } \\[5pt] &=& \frac{1-\sqrt{5} }{4} +a \cdot 1 +a \cdot \frac{1-\sqrt{5} }{4} +a^2\cdot \frac{1-\sqrt{5} }{4} \\[5pt] &=& a+\frac{1-\sqrt{5} }{4}(1+a+a^2) \\[5pt] \end{eqnarray}となります。もともと、 $a=\dfrac{1+\sqrt{5} }{2}$ は $a^2-a-1=0$ の解だったので、 $1+a+a^2=1+a+a+1=2(1+a)$ だから \begin{eqnarray} & & a+\frac{1-\sqrt{5} }{4}(1+a+a^2) \\[5pt] &=& a+\frac{1-\sqrt{5} }{2}(1+a) \\[5pt] &=& \frac{1+\sqrt{5} }{2}+\frac{1-\sqrt{5} }{2}\cdot \frac{3+\sqrt{5} }{2} \\[5pt] &=& \frac{1+\sqrt{5} }{2}+\frac{3-5-2\sqrt{5} }{4} \\[5pt] &=& 0 \end{eqnarray}となります。

解答

シス：90

解答編つづき

　最後に、面 $\mathrm{ A_2C_1DEB_2 }$ に着目する。\[ \overrightarrow{ \mathrm{ B_2D } }=\mybox{ウ} \overrightarrow{ \mathrm{ A_2C_1 } } =\overrightarrow{ \mathrm{ OB_1 } } \]であることに注意すると、4点 $\mathrm{ O, B_1, D, B_2 }$ は同一平面上にあり、四角形 $\mathrm{ OB_1DB_2 }$ は $\myBox{セ}$ ことがわかる。

$\mybox{セ}$ の解答群

　0: 正方形である
　1: 正方形ではないが、長方形である
　2: 正方形ではないが、ひし形である
　3: 長方形でもひし形でもないが、平行四辺形である
　4: 平行四辺形ではないが、台形である
　5: 台形でない

ただし、少なくとも一組の対辺が平行な四角形を台形という。

解説

ここまでと同じように考えると、 $\overrightarrow{ \mathrm{ B_2D } }=a\overrightarrow{ \mathrm{ A_2C_1 } }$ と書けるため、 $\overrightarrow{ \mathrm{ OB_2 } }$ と等しくなります。これから、線分 $\mathrm{ B_2D }$ と線分 $\mathrm{ OB_1 }$ は長さが等しくて平行であることがわかります。そのため、少なくとも、四角形 $\mathrm{ OB_1DB_2 }$ は平行四辺形だとわかります。

そもそも、図から、 $\mathrm{ OB_2, B_2D, DB_1, B_1O }$ はどれも正五角形の対角線だから、長さは $a$ です。少なくともひし形であることもわかります（これは別にベクトルを使わなくてもわかります）。

後は、角がどうなっているかを考えるだけです。スのところで、 $\overrightarrow{ \mathrm{ OB_1 } }$ と $\overrightarrow{ \mathrm{ OB_2 } }$ の内積が $0$ であることを求めたので、これから $\angle \mathrm{ B_2OB_1 }$ が $90^{\circ}$ だとわかります。

こうして、四角形 $\mathrm{ OB_1DB_2 }$ は正方形であることがわかります。