共通テスト 数学II・数学B 2021年度 第2問 解説
【必答問題】
問題編
問題
(1) 座標平面上で、次の二つの2次関数のグラフについて考える。
\begin{eqnarray} y&=& 3x^2+2x+3\quad \cdots ① \\[5pt] y&=& 2x^2+2x+3\quad \cdots ② \end{eqnarray}①, ②の2次関数のグラフには、次の共通点がある。
共通点
- $y$ 軸との交点の $y$ 座標は $\myBox{ア}$ である。
- $y$ 軸との交点における接線の方程式は $y=\myBox{イ}x+\myBox{ウ}$ である。
次の 0 ~ 5 の2次関数のグラフのうち、 $y$ 軸との交点における接線の方程式が $y=\mybox{イ}x+\mybox{ウ}$ となるものは $\myBox{エ}$ である。
$\mybox{エ}$ の解答群
0: $y=3x^2-2x-3$
1: $y=-3x^2+2x-3$
2: $y=2x^2+2x-3$
3: $y=2x^2-2x+3$
4: $y=-x^2+2x+3$
5: $y=-x^2-2x+3$$a,b,c$ を $0$ でない実数とする。
曲線 $y=ax^2+bx+c$ 上の点 $\left(0,\myBox{オ}\right)$ における接線を $\ell$ とすると、その方程式は $y=\myBox{カ}x+\myBox{キ}$ である。
接線 $\ell$ と $x$ 軸との交点の $x$ 座標は $\dfrac{\myBox{クケ} }{\myBox{コ} }$ である。
$a,b,c$ が正の実数であるとき、曲線 $y=ax^2+bx+c$ と接線 $\ell$ および直線 $x=\dfrac{\mybox{クケ} }{\mybox{コ} }$ で囲まれた図形の面積を $S$ とすると\[ S=\dfrac{ac^{\myBox{サ} }}{\myBox{シ}\ b^{\myBox{ス} }} \quad\cdots③ \]である。
③において、 $a=1$ とし、 $S$ の値が一定となるように正の実数 $b,c$ の値を変化させる。このとき、 $b$ と $c$ の関係を表すグラフの概形は $\myBox{セ}$ である。
$\mybox{セ}$ については、最も適当なものを、次の 0 から 5 のうちから一つ選べ。
(注意:少し見にくいですが、軸上の点は白丸です)
0 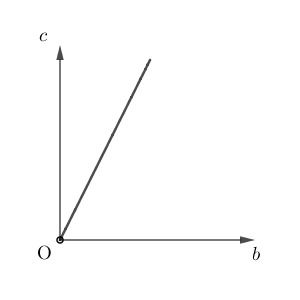
1 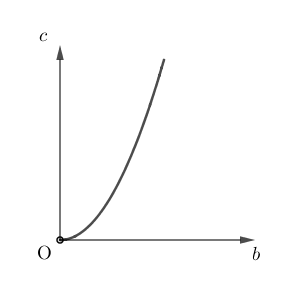
2 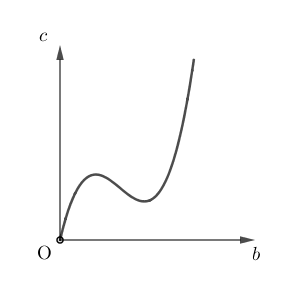
3 
4 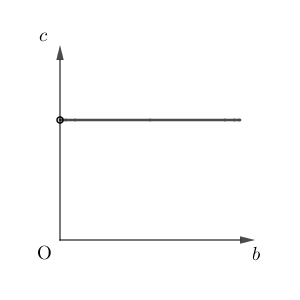
5 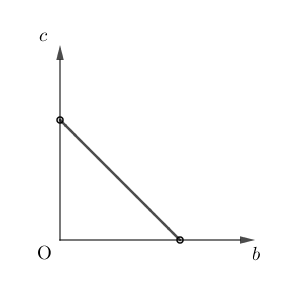
(2) 座標平面上で、次の三つの3次関数のグラフについて考える。
\begin{eqnarray} y &=& 4x^3+2x^2+3x+5 \quad \cdots ④ \\[5pt] y &=& -2x^3+7x^2+3x+5 \quad \cdots ⑤ \\[5pt] y &=& 5x^3-x^2+3x+5 \quad \cdots ⑥ \\[5pt] \end{eqnarray}④, ⑤, ⑥の3次関数のグラフには次の共通点がある。
共通点
- $y$ 軸との交点の $y$ 座標は $\myBox{ソ}$ である。
- $y$ 軸との交点における接線の方程式は $y=\myBox{タ}x+\myBox{チ}$ である。
$a,b,c,d$ を $0$ でない実数とする。
曲線 $y=ax^3+bx^2+cx+d$ 上の点 $\left(0,\myBox{ツ}\right)$ における接線の方程式は $y=\myBox{テ}x+\myBox{ト}$ である。
次に、 $f(x)=ax^3+bx^2+cx+d$, $g(x)=\mybox{テ}x+\mybox{ト}$ とし、 $f(x)-g(x)$ について考える。
$h(x)=f(x)-g(x)$ とおく。 $a,b,c,d$ が正の実数であるとき、 $y=h(x)$ のグラフの概形は $\myBox{ナ}$ である。
$y=f(x)$ のグラフと $y=g(x)$ のグラフの共有点の $x$ 座標は $\dfrac{\myBox{ニヌ} }{\myBox{ネ} }$ と $\myBox{ノ}$ である。また、 $x$ が $\dfrac{\mybox{ニヌ} }{\mybox{ノ} }$ と $\mybox{ノ}$ の間を動くとき、 $|f(x)-g(x)|$ の値が最大となるのは、 $x=\dfrac{\myBox{ハヒフ} }{\myBox{ヘホ} }$ のときである。
$\mybox{ナ}$ については、最も適当なものを、次の 0 ~ 5 のうちから一つ選べ。
0 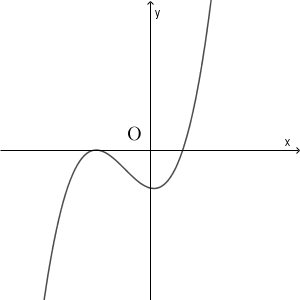
1 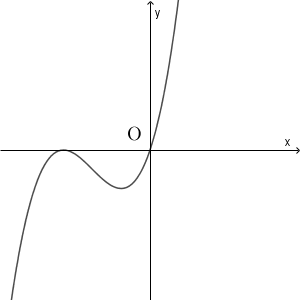
2 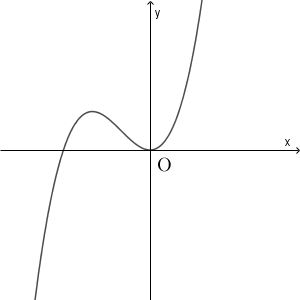
3 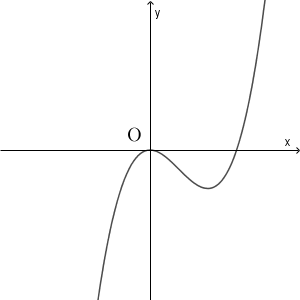
4 
5 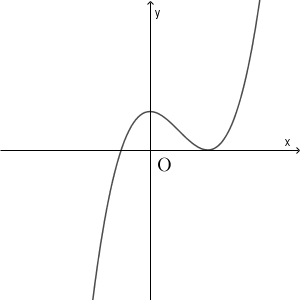
考え方
文字が入ったまま計算するのは慣れていないと難しいかもしれません。面積 $S$ を求めるために図をかきたくなりますが、値がわからないので具体的な図はかけません。しかし、面積を求めるのに必要な位置関係さえわかれば、面積を求めることはできます。
(2)のグラフを求める問題は、 $x$ 軸との共有点について考えるといいでしょう。
解答編
問題
(1) 座標平面上で、次の二つの2次関数のグラフについて考える。
\begin{eqnarray} y&=& 3x^2+2x+3\quad \cdots ① \\[5pt] y&=& 2x^2+2x+3\quad \cdots ② \end{eqnarray}①, ②の2次関数のグラフには、次の共通点がある。
共通点
- $y$ 軸との交点の $y$ 座標は $\myBox{ア}$ である。
- $y$ 軸との交点における接線の方程式は $y=\myBox{イ}x+\myBox{ウ}$ である。
次の 0 ~ 5 の2次関数のグラフのうち、 $y$ 軸との交点における接線の方程式が $y=\mybox{イ}x+\mybox{ウ}$ となるものは $\myBox{エ}$ である。
$\mybox{エ}$ の解答群
0: $y=3x^2-2x-3$
1: $y=-3x^2+2x-3$
2: $y=2x^2+2x-3$
3: $y=2x^2-2x+3$
4: $y=-x^2+2x+3$
5: $y=-x^2-2x+3$
解説
$y$ 軸との交点の $y$ 座標は、 $x=0$ を代入すればよく、 $y=3$ だとわかります。
また、 $y=3x^2+2x+3$ を微分すると $y'=3x+2$ なので、 $y$ 軸との交点における接線の傾きは $2$ です。なので、接線の方程式は $y=2x+3$ となります。
次に、選択肢の中で、 $y$ 軸との交点における接線の方程式が $y=2x+3$ になるものを考えます。まず、2次関数のグラフが $(0,3)$ を通らないものは除外できるので、 3 ~ 5 のどれかになります。接線の傾きは、微分して $x=0$ を代入したときの値なので、これが $2$ となるのは、選択肢4の $y=-x^2+2x+3$ しかありません。
解答
ア:3
イウ:23
エ:4
解答編 つづき
$a,b,c$ を $0$ でない実数とする。
曲線 $y=ax^2+bx+c$ 上の点 $\left(0,\myBox{オ}\right)$ における接線を $\ell$ とすると、その方程式は $y=\myBox{カ}x+\myBox{キ}$ である。
接線 $\ell$ と $x$ 軸との交点の $x$ 座標は $\dfrac{\myBox{クケ} }{\myBox{コ} }$ である。
解説
$x=0$ のとき $y=c$ です。また、 $y=ax^2+bx+c$ を微分すると $y'=2x+b$ なので、 $x=0$ とすると $b$ になります。よって、接線 $\ell$ の方程式は $y=bx+c$ となります。
接線 $\ell$ と $x$ 軸との交点の $x$ 座標は
\begin{eqnarray}
0 &=& bx+c \\[5pt]
x &=& -\frac{c}{b} \\[5pt]
\end{eqnarray}となります。
解答
オ:c
カキ:bc
クケコ:-cb
解答編 つづき
$a,b,c$ が正の実数であるとき、曲線 $y=ax^2+bx+c$ と接線 $\ell$ および直線 $x=\dfrac{\mybox{クケ} }{\mybox{コ} }$ で囲まれた図形の面積を $S$ とすると\[ S=\dfrac{ac^{\myBox{サ} }}{\myBox{シ}\ b^{\myBox{ス} }} \quad\cdots③ \]である。
解説
値がわからないので図がかきづらいですが、積分をするには位置関係がわかればいいです。 $a$ が正なので、放物線は下に凸です。そのため、接線のほうが下にあります。

$b,c$ は正なので、直線 $x=-\dfrac{c}{b}$ は $y$ 軸より左側にあります。こうして、 $S$ は、 $ax^2+bx+c$ から $bx+c$ を引いたものを、 $-\dfrac{c}{b}$ から $0$ まで積分すれば求められます。なので
\begin{eqnarray}
S
&=&
\int_{-\frac{c}{b} }^0 ax^2 dx \\[5pt]
&=&
\left[\frac{ax^3}{3}\right]_{-\frac{c}{b} }^0 \\[5pt]
&=&
-\frac{a}{3}\cdot \left(-\dfrac{c}{b}\right)^3 \\[5pt]
&=&
\frac{ac^3}{3b^3} \\[5pt]
\end{eqnarray}となることがわかります。
解答
サシス:333
解答編 つづき
③において、 $a=1$ とし、 $S$ の値が一定となるように正の実数 $b,c$ の値を変化させる。このとき、 $b$ と $c$ の関係を表すグラフの概形は $\myBox{セ}$ である。
$\mybox{セ}$ については、最も適当なものを、次の 0 から 5 のうちから一つ選べ。
(注意:少し見にくいですが、軸上の点は白丸です)
0 
1 
2 
3 
4 
5 
解説
先ほど求めた面積\[ S=\dfrac{ac^3}{3b^3} \]について、 $a=1$ で $S$ が一定となる場合を考えます。このとき、 $b,c$ は実数なので、
\begin{eqnarray}
S &=& \frac{c^3}{3b^3} \\[5pt]
3Sb^3 &=& c^3 \\[5pt]
c &=& \sqrt[3]{3S} b \\[5pt]
\end{eqnarray}となります。つまり、 $S$ が一定であれば、 $c$ は $b$ に比例するので、グラフは 0 となります。
解答
セ:0
解答編 つづき
(2) 座標平面上で、次の三つの3次関数のグラフについて考える。
\begin{eqnarray} y &=& 4x^3+2x^2+3x+5 \quad \cdots ④ \\[5pt] y &=& -2x^3+7x^2+3x+5 \quad \cdots ⑤ \\[5pt] y &=& 5x^3-x^2+3x+5 \quad \cdots ⑥ \\[5pt] \end{eqnarray}④, ⑤, ⑥の3次関数のグラフには次の共通点がある。
共通点
- $y$ 軸との交点の $y$ 座標は $\myBox{ソ}$ である。
- $y$ 軸との交点における接線の方程式は $y=\myBox{タ}x+\myBox{チ}$ である。
$a,b,c,d$ を $0$ でない実数とする。
曲線 $y=ax^3+bx^2+cx+d$ 上の点 $\left(0,\myBox{ツ}\right)$ における接線の方程式は $y=\myBox{テ}x+\myBox{ト}$ である。
解説
④~⑥については、$x=0$ とすると、どれも $y=5$ となります。 $y$ 軸との交点の $y$ 座標は $5$ です。
また、微分して $x=0$ を代入すると、どれも $3$ になります。よって、接線の方程式は $y=3x+5$ と求められます。
$y=ax^3+bx^3+cx+d$ の場合は、 $x=0$ とすると $y=d$ です。また、微分すると $y'=3x^2+2bx+c$ なので、 $x=0$ とすると $y'=c$ です。よって、接線の方程式は $y=cx+d$ となります。
解答
ソ:5
タチ:35
ツ:d
テト:cd
解答編 つづき
次に、 $f(x)=ax^3+bx^2+cx+d$, $g(x)=\mybox{テ}x+\mybox{ト}$ とし、 $f(x)-g(x)$ について考える。
$h(x)=f(x)-g(x)$ とおく。 $a,b,c,d$ が正の実数であるとき、 $y=h(x)$ のグラフの概形は $\myBox{ナ}$ である。
$y=f(x)$ のグラフと $y=g(x)$ のグラフの共有点の $x$ 座標は $\dfrac{\myBox{ニヌ} }{\myBox{ネ} }$ と $\myBox{ノ}$ である。また、 $x$ が $\dfrac{\mybox{ニヌ} }{\mybox{ノ} }$ と $\mybox{ノ}$ の間を動くとき、 $|f(x)-g(x)|$ の値が最大となるのは、 $x=\dfrac{\myBox{ハヒフ} }{\myBox{ヘホ} }$ のときである。
$\mybox{ナ}$ については、最も適当なものを、次の 0 ~ 5 のうちから一つ選べ。
0 
1 
2 
3 
4 
5 
解説
$f(x)=ax^3+bx^2+cx+d$, $g(x)=cx+d$ なので、 $h(x)=f(x)-g(x)=ax^3+bx^2$ となります。これは\[ h(x)=x^2(ax+b) \]と変形できます。このことから、方程式 $h(x)=0$ において、 $x=0$ は重解で、もう1つの解は $-\dfrac{b}{a}$ となることがわかります。 $a,b$ はともに正なので、この値は負です。
よって、グラフは $x=0$ で接していて、 $x$ 軸の負の部分とも交わっているものを選べばいいです。 2 しかありません。
$y=f(x)$ のグラフと $y=g(x)$ のグラフの共有点の $x$ 座標とは、 $y=h(x)$ と $x$ 軸との共有点の $x$ 座標と一致するので、 $\dfrac{-b}{a}$ と $0$ だとわかります。また、 $x$ がこの間を動くとき、 $|f(x)-g(x)|$ の値が最大となるのは、 2 のグラフを見ると、 $y=h(x)$ が極大値をとるときだとわかります。
$h(x)=ax^3+bx^2$ なので、 $h'(x)=3ax^2+2bx$ だから、 $h'(x)=0$ とすると $x=0,-\dfrac{2b}{3a}$ となります。 $x=-\dfrac{2b}{3a}$ の前後で $h'(x)$ の符号は正から負にかわるため、ここで極大をとることがわかり、 $|h(x)|$ が最大になることもわかります。
こうして、 $|f(x)-g(x)|$ が最大となるのは $x=\dfrac{-2b}{3a}$ のときとなります。
解答
ナ:2
ニヌネ:-ba
ノ:0
ハヒフヘホ:-2b3a





