共通テスト数学I・数学A 2023年度第5問解説

🕒 2023/01/16 🔄 2023/05/01

【第3問～第5問から2問選択】

問題編

問題

(1) 円 $\mathrm{O}$ に対して、次の手順１で作図を行う。

手順１
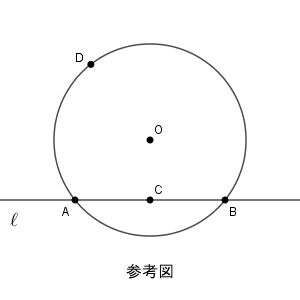
(Step 1)　円 $\mathrm{O}$ と異なる2点で交わり、中心 $\mathrm{O}$ を通らない直線 $\ell$ を引く。円 $\mathrm{O}$ と直線 $\ell$ との交点を $\mathrm{A, B}$ とし、線分 $\mathrm{AB}$ の中点 $\mathrm{C}$ をとる。

(Step 2)　円 $\mathrm{O}$ の周上に、点 $\mathrm{D}$ を $\angle \mathrm{COD}$ が鈍角となるようにとる。直線 $\mathrm{CD}$ を引き、円 $\mathrm{O}$ との交点で $\mathrm{D}$ とは異なる点を $\mathrm{E}$ とする。

(Step 3)　点 $\mathrm{D}$ を通り直線 $\mathrm{OC}$ に垂直な直線を引き、直線 $\mathrm{OC}$ との交点を $\mathrm{F}$ とし、円 $\mathrm{O}$ との交点で $\mathrm{D}$ とは異なる点を $\mathrm{G}$ とする。

(Step 4)　点 $\mathrm{G}$ における円 $\mathrm{O}$ の接線を引き、直線 $\ell$ との交点を $\mathrm{H}$ とする。

　このとき、直線 $\ell$ と点 $\mathrm{D}$ の位置によらず、直線 $\mathrm{EH}$ は円 $\mathrm{O}$ の接線である。このことは、次の構想に基づいて、後のように説明できる。

構想
　直線 $\mathrm{EH}$ が円 $\mathrm{O}$ の接線であることを証明するためには、 $\angle \mathrm{OEH}=\myBox{アイ}^{\circ}$ であることを示せばよい。

　手順１の (Step 1) と (Step 4) により、4点 $\mathrm{C,\ G,\ H,}\ \dBox{ウ}$ は同一円周上にあることがわかる。よって、 $\angle \mathrm{CHG}=\dBox{エ}$ である。一方、点 $\mathrm{E}$ は円 $\mathrm{O}$ の周上にあることから、 $\dbox{エ}=\dBox{オ}$ がわかる。よって、 $\angle \mathrm{CHG}=\dbox{オ}$ であるので、4点 $\mathrm{C,\ G,\ H,\ }\dBox{カ}$ は同一円周上にある。この円が点 $\dbox{ウ}$ を通ることにより、 $\angle \mathrm{OEH}=\mybox{アイ}^{\circ}$ を示すことができる。

$\dbox{ウ}$ の解答群

　0: $\mathrm{B}$
　1: $\mathrm{D}$
　2: $\mathrm{F}$
　3: $\mathrm{O}$

$\dbox{エ}$ の解答群

　0: $\angle \mathrm{AFC}$
　1: $\angle \mathrm{CDF}$
　2: $\angle \mathrm{CGH}$
　3: $\angle \mathrm{CBO}$
　4: $\angle \mathrm{FOG}$

$\dbox{オ}$ の解答群

　0: $\angle \mathrm{AED}$
　1: $\angle \mathrm{ADE}$
　2: $\angle \mathrm{BOE}$
　3: $\angle \mathrm{DEG}$
　4: $\angle \mathrm{EOH}$

$\dbox{カ}$ の解答群

　0: $\mathrm{A}$
　1: $\mathrm{D}$
　2: $\mathrm{E}$
　3: $\mathrm{F}$

(2) 円 $\mathrm{O}$ に対して、(1)の手順１とは直線 $\ell$ の引き方を変え、次の手順２で作図を行う。

手順２
(Step 1)　円 $\mathrm{O}$ と共有点をもたない直線 $\ell$ を引く。中心 $\mathrm{O}$ から直線 $\ell$ に垂直な直線を引き、直線 $\ell$ との交点を $\mathrm{P}$ をとる。

(Step 2)　円 $\mathrm{O}$ の周上に、点 $\mathrm{Q}$ を $\angle \mathrm{POQ}$ が鈍角となるようにとる。直線 $\mathrm{PQ}$ を引き、円 $\mathrm{O}$ との交点で $\mathrm{Q}$ とは異なる点を $\mathrm{R}$ とする。

(Step 3)　点 $\mathrm{Q}$ を通り直線 $\mathrm{OP}$ に垂直な直線を引き、円 $\mathrm{O}$ との交点で $\mathrm{Q}$ とは異なる点を $\mathrm{S}$ とする。

(Step 4)　点 $\mathrm{S}$ における円 $\mathrm{O}$ の接線を引き、直線 $\ell$ との交点を $\mathrm{T}$ とする。

　このとき、 $\angle\mathrm{PTS}=\dBox{キ}$ である。

　円 $\mathrm{O}$ の半径が $\sqrt{5}$ で、 $\mathrm{OT}=3\sqrt{6}$ であったとすると、3点 $\mathrm{O,P,R}$ を通る円の半径は $\dfrac{\myBox{ク}\sqrt{\myBox{ケ}}}{\myBox{コ}}$ であり、 $\mathrm{RT}=\myBox{サ}$ である。

$\dbox{キ}$ の解答群

　0: $\angle \mathrm{PQS}$
　1: $\angle \mathrm{PST}$
　2: $\angle \mathrm{QPS}$
　3: $\angle \mathrm{QRS}$
　4: $\angle \mathrm{SRT}$

考え方

円周角の定理やその逆などを用いて考えていきます。後半は前半で示した内容を応用して考えると、似たような結論が得られます。最後の計算は、ここまでの証明でわかっている角を考えれば、何をすればいいかが見えてくるでしょう。

解答編

問題

(1) 円 $\mathrm{O}$ に対して、次の手順１で作図を行う。

手順１
(Step 1)　円 $\mathrm{O}$ と異なる2点で交わり、中心 $\mathrm{O}$ を通らない直線 $\ell$ を引く。円 $\mathrm{O}$ と直線 $\ell$ との交点を $\mathrm{A, B}$ とし、線分 $\mathrm{AB}$ の中点 $\mathrm{C}$ をとる。

(Step 2)　円 $\mathrm{O}$ の周上に、点 $\mathrm{D}$ を $\angle \mathrm{COD}$ が鈍角となるようにとる。直線 $\mathrm{CD}$ を引き、円 $\mathrm{O}$ との交点で $\mathrm{D}$ とは異なる点を $\mathrm{E}$ とする。

(Step 3)　点 $\mathrm{D}$ を通り直線 $\mathrm{OC}$ に垂直な直線を引き、直線 $\mathrm{OC}$ との交点を $\mathrm{F}$ とし、円 $\mathrm{O}$ との交点で $\mathrm{D}$ とは異なる点を $\mathrm{G}$ とする。

(Step 4)　点 $\mathrm{G}$ における円 $\mathrm{O}$ の接線を引き、直線 $\ell$ との交点を $\mathrm{H}$ とする。

　このとき、直線 $\ell$ と点 $\mathrm{D}$ の位置によらず、直線 $\mathrm{EH}$ は円 $\mathrm{O}$ の接線である。このことは、次の構想に基づいて、後のように説明できる。

構想
　直線 $\mathrm{EH}$ が円 $\mathrm{O}$ の接線であることを証明するためには、 $\angle \mathrm{OEH}=\myBox{アイ}^{\circ}$ であることを示せばよい。

　手順１の (Step 1) と (Step 4) により、4点 $\mathrm{C,\ G,\ H,}\ \dBox{ウ}$ は同一円周上にあることがわかる。よって、 $\angle \mathrm{CHG}=\dBox{エ}$ である。一方、点 $\mathrm{E}$ は円 $\mathrm{O}$ の周上にあることから、 $\dbox{エ}=\dBox{オ}$ がわかる。よって、 $\angle \mathrm{CHG}=\dbox{オ}$ であるので、4点 $\mathrm{C,\ G,\ H,\ }\dBox{カ}$ は同一円周上にある。この円が点 $\dbox{ウ}$ を通ることにより、 $\angle \mathrm{OEH}=\mybox{アイ}^{\circ}$ を示すことができる。

$\dbox{ウ}$ の解答群

　0: $\mathrm{B}$
　1: $\mathrm{D}$
　2: $\mathrm{F}$
　3: $\mathrm{O}$

$\dbox{エ}$ の解答群

　0: $\angle \mathrm{AFC}$
　1: $\angle \mathrm{CDF}$
　2: $\angle \mathrm{CGH}$
　3: $\angle \mathrm{CBO}$
　4: $\angle \mathrm{FOG}$

$\dbox{オ}$ の解答群

　0: $\angle \mathrm{AED}$
　1: $\angle \mathrm{ADE}$
　2: $\angle \mathrm{BOE}$
　3: $\angle \mathrm{DEG}$
　4: $\angle \mathrm{EOH}$

$\dbox{カ}$ の解答群

　0: $\mathrm{A}$
　1: $\mathrm{D}$
　2: $\mathrm{E}$
　3: $\mathrm{F}$

解説

直線 $\mathrm{EH}$ が円 $\mathrm{O}$ の接線であることを証明するには、 $\angle\mathrm{OEH}=90^{\circ}$ であることを示せばいいです。図は次のようになっています。

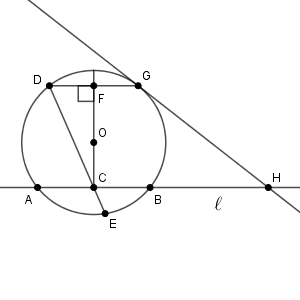
Step1より、$\mathrm{OC}$ と $\mathrm{AH}$ は垂直です。また、Step4より、$\mathrm{OG}$ と $\mathrm{GH}$ は垂直です。なので、 $\angle \mathrm{OCH}=\angle \mathrm{OGH} = 90^{\circ}$ なので、4点 $\mathrm{C,G,H,O}$ は同一円周上にあることがわかります。これより、円に内接する四角形は、どの内角についても、その対角の外角に等しいので、 $\angle \mathrm{BHG}$ は $\angle \mathrm{FOG}$ と等しいことがわかります。

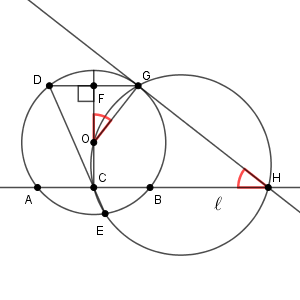
一方、 $\triangle \mathrm{ODG}$ は二等辺三角形なので、 $\angle \mathrm{DOG}=2\angle \mathrm{FOG}$ です。また、円周角の定理より、 $\angle \mathrm{DOG}=2\angle \mathrm{DEG}$ なので、 $\angle\mathrm{FOG}=\angle \mathrm{DEG}$ であることがわかります。

よって、 $\angle \mathrm{CHG}=\angle \mathrm{DEG}=\angle \mathrm{CEG}$ が得られます。円周角の定理の逆から、4点 $\mathrm{C,G,H,E}$ が同一円周上にあることわかります。

このことから、 $\mathrm{O,E}$ は三角形 $\mathrm{CGH}$ の外接円上にあるので、 $\mathrm{C,G,H,E,O}$ は同一円周上にあることがわかり、\[ \angle \mathrm{OEH}=\angle \mathrm{OCH}=90^{\circ} \]となることがわかります。

解答

アイ：90 (2点)
ウ：3 (2点)
エ：4 (3点)
オ：3 (3点)
カ：2 (2点)

解答編　つづき

問題

(2) 円 $\mathrm{O}$ に対して、(1)の手順１とは直線 $\ell$ の引き方を変え、次の手順２で作図を行う。

手順２
(Step 1)　円 $\mathrm{O}$ と共有点をもたない直線 $\ell$ を引く。中心 $\mathrm{O}$ から直線 $\ell$ に垂直な直線を引き、直線 $\ell$ との交点を $\mathrm{P}$ をとる。

(Step 2)　円 $\mathrm{O}$ の周上に、点 $\mathrm{Q}$ を $\angle \mathrm{POQ}$ が鈍角となるようにとる。直線 $\mathrm{PQ}$ を引き、円 $\mathrm{O}$ との交点で $\mathrm{Q}$ とは異なる点を $\mathrm{R}$ とする。

(Step 3)　点 $\mathrm{Q}$ を通り直線 $\mathrm{OP}$ に垂直な直線を引き、円 $\mathrm{O}$ との交点で $\mathrm{Q}$ とは異なる点を $\mathrm{S}$ とする。

(Step 4)　点 $\mathrm{S}$ における円 $\mathrm{O}$ の接線を引き、直線 $\ell$ との交点を $\mathrm{T}$ とする。

　このとき、 $\angle\mathrm{PTS}=\dBox{キ}$ である。

　円 $\mathrm{O}$ の半径が $\sqrt{5}$ で、 $\mathrm{OT}=3\sqrt{6}$ であったとすると、3点 $\mathrm{O,P,R}$ を通る円の半径は $\dfrac{\myBox{ク}\sqrt{\myBox{ケ}}}{\myBox{コ}}$ であり、 $\mathrm{RT}=\myBox{サ}$ である。

$\dbox{キ}$ の解答群

　0: $\angle \mathrm{PQS}$
　1: $\angle \mathrm{PST}$
　2: $\angle \mathrm{QPS}$
　3: $\angle \mathrm{QRS}$
　4: $\angle \mathrm{SRT}$

解説

(2)
$\mathrm{SQ}$ の中点を $\mathrm{M}$ とすると、図は次のようになっています。

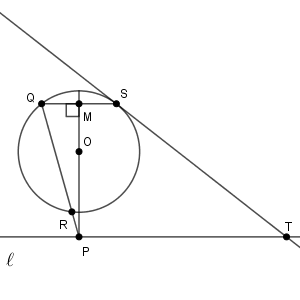
(1)と同様にすれば、4点 $\mathrm{O,S,T,P}$ が同一円周上にあることから、
\begin{eqnarray} \angle \mathrm{PTS} &=& \angle \mathrm{MOS} \\[5pt] &=& \frac{1}{2} \angle \mathrm{QOS} \\[5pt] &=& \angle \mathrm{QRS} \\[5pt] \end{eqnarray}となります。これより、四角形 $\mathrm{PRST}$ が円に内接することがわかります。よって、 $\mathrm{O,S,T,P,R}$ は同一円周上にあることがわかり、 $\angle \mathrm{ORT}=\angle \mathrm{OPT}=90^{\circ}$ だから、直線 $\mathrm{RT}$ は円 $\mathrm{O}$ の接線だとわかります。

問題文にある、 $\mathrm{O,P,R}$ を通る円は、他に $\mathrm{T}$ も通ります。 $\angle\mathrm{ORT}=90^{\circ}$ なので、 $\mathrm{OT}$ がこの円の直径になることから、半径は\[ \frac{3\sqrt{6}}{2} \] だとわかります。また、 $\angle \mathrm{ORT}=90^{\circ}$ なので、三平方の定理から
\begin{eqnarray} \mathrm{RT} &=& \sqrt{ \mathrm{OT^2}-\mathrm{OR^2} } \\[5pt] &=& \sqrt{ 54-5 } \\[5pt] &=& 7 \end{eqnarray}と求められます。