共通テスト 数学I・数学A 2023年度 第2問 [1] 解説

【必答問題】

問題編

問題

　太郎さんは、総務省が公表している2020年の家計調査の結果を用いて、地域による食文化の違いについて考えている。家計調査における調査地点は、都道府県庁所在市および政令指定都市（都道府県庁所在市を除く）であり、合計52市である。家計調査の結果の中でも、スーパーマーケットなどで販売されている調理食品の「二人以上の世帯の１世帯当たり年間支出金額（以下、支出金額、単位は円）」を分析することにした。以下においては、52市の調理食品の支出金額をデータとして用いる。

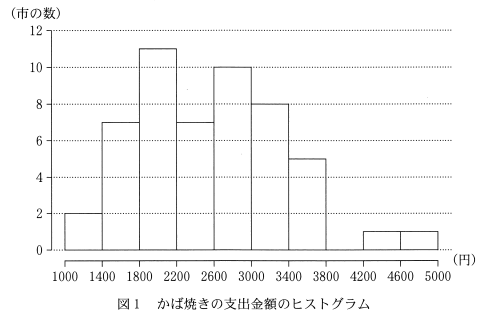
　太郎さんは調理食品として、最初にうなぎのかば焼き（以下、かば焼き）に着目し、図１にように52市におけるかば焼きの支出金額のヒストグラムを作成した。ただし、ヒストグラムの各階級の区間は、左側の数値を含み、右側の数値を含まない。

　なお、以下の図や表については、総務省のWebページをもとに作成している。

(1) 図１から次のことが読み取れる。

• 第1四分位数が含まれる階級は $\dBox{ア}$ である。
• 第3四分位数が含まれる階級は $\dBox{イ}$ である。
• 四分位範囲は $\dBox{ウ}$ 。

$\dbox{ア}$ $\dbox{イ}$ の解答群（同じものを繰り返し選んでもよい。）

　0: 1000以上 1400未満
　1: 1400以上 1800未満
　2: 1800以上 2200未満
　3: 2200以上 2600未満
　4: 2600以上 3000未満
　5: 3000以上 3400未満
　6: 3400以上 3800未満
　7: 3800以上 4200未満
　8: 4200以上 4600未満
　9: 4600以上 5000未満

$\dbox{ウ}$ の解答群

　0: 800より小さい
　1: 800より大きく 1600より小さい
　2: 1600より大きく 2400より小さい
　3: 2400より大きく 3200より小さい
　4: 3200より大きく 4000より小さい
　5: 4000より大きい

(2) 太郎さんは、東西での地域による食文化の違いを調べるために、52市を東側の地域E（19市）と西側の地域W（33市）の二つに分けて考えることにした。

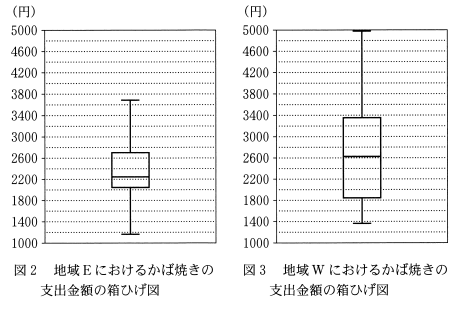
(i) 地域Eと地域Wについて、かば焼きの支出金額の箱ひげ図を、図２、３のようにそれぞれ作成した。

　かば焼きの支出金額について、図２と図３から読み取れることとして、次の 0 ～ 3 のうち、正しいものは $\dBox{エ}$ である。

$\dbox{エ}$ の解答群

　0: 地域Eにおいて、小さい方から5番目は2000以下である。
　1: 地域Eと地域Wの範囲は等しい。
　2: 中央値は、地域Eより地域Wの方が大きい。
　3: 2600未満の市の割合は、地域Eより地域Wの方が大きい。

(ii) 太郎さんは、地域Eと地域Wのデータの散らばりの度合いを数値でとらえようと思い、それぞれの分散を考えることにした。地域Eにおけるかば焼きの支出の分散は、地域Eのそれぞれの市におけるかば焼きの支出金額の偏差の $\dBox{オ}$ である。

$\dbox{オ}$ の解答群

　0: 2乗を合計した値
　1: 絶対値を合計した値
　2: 2乗を合計して地域Eの市の数で割った値
　3: 絶対値を合計して地域Eの市の数で割った値
　4: 2乗を合計して地域Eの市の数で割った値の平方根のうち、正のもの
　5: 絶対値を合計して地域Eの市の数で割った値の平方根のうち、正のもの

(3) 太郎さんは、(2)で考えた地域Eにおける、やきとりの支出金額についても調べることにした。

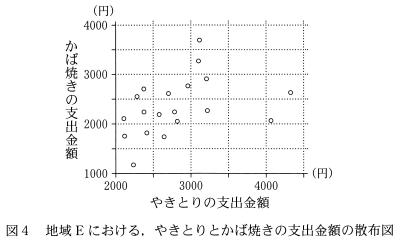
　ここでは地域Eにおいて、やきとりの支出金額が増加すれば、かば焼きの支出金額も増加する傾向があるのではないかと考え、まず図４のように、地域Eにおける、やきとりとかば焼きの支出金額の散布図を作成した。そして、相関係数を計算するために、表１のように平均値、分散、標準偏差および共分散を算出した。ただし、共分散は地域Eのそれぞれの市における、やきとりの支出金額の偏差とかば焼きの支出金額の偏差との積の平均値である。

表１　地域Eにおける、やきとりとかば焼きの支出金額の平均値、分散、標準偏差および共分散

	平均値	分散	標準偏差	共分散
やきとりの支出金額	2810	348100	590	124000
かば焼きの支出金額	2350	324900	570

　表１を用いると、地域Eにおける、やきとりの支出金額とかば焼きの支出金額の相関係数は $\dBox{カ}$ である。

$\dbox{カ}$ については、最も適当なものを、次の 0 ～ 9 のうちから一つ選べ。
　0: $-0.62$
　1: $-0.50$
　2: $-0.37$
　3: $-0.19$
　4: $-0.02$
　5: $0.02$
　6: $0.19$
　7: $0.37$
　8: $0.50$
　9: $0.62$

考え方

言葉の定義がわかっているか、グラフから必要な情報が読み取れるか、が問われており、全体的に基本的な内容です。

【必答問題】

解答編

問題

　太郎さんは、総務省が公表している2020年の家計調査の結果を用いて、地域による食文化の違いについて考えている。家計調査における調査地点は、都道府県庁所在市および政令指定都市（都道府県庁所在市を除く）であり、合計52市である。家計調査の結果の中でも、スーパーマーケットなどで販売されている調理食品の「二人以上の世帯の１世帯当たり年間支出金額（以下、支出金額、単位は円）」を分析することにした。以下においては、52市の調理食品の支出金額をデータとして用いる。

　太郎さんは調理食品として、最初にうなぎのかば焼き（以下、かば焼き）に着目し、図１にように52市におけるかば焼きの支出金額のヒストグラムを作成した。ただし、ヒストグラムの各階級の区間は、左側の数値を含み、右側の数値を含まない。

　なお、以下の図や表については、総務省のWebページをもとに作成している。



(1) 図１から次のことが読み取れる。

• 第1四分位数が含まれる階級は $\dBox{ア}$ である。
• 第3四分位数が含まれる階級は $\dBox{イ}$ である。
• 四分位範囲は $\dBox{ウ}$ 。

$\dbox{ア}$ $\dbox{イ}$ の解答群（同じものを繰り返し選んでもよい。）

　0: 1000以上 1400未満
　1: 1400以上 1800未満
　2: 1800以上 2200未満
　3: 2200以上 2600未満
　4: 2600以上 3000未満
　5: 3000以上 3400未満
　6: 3400以上 3800未満
　7: 3800以上 4200未満
　8: 4200以上 4600未満
　9: 4600以上 5000未満

$\dbox{ウ}$ の解答群

　0: 800より小さい
　1: 800より大きく 1600より小さい
　2: 1600より大きく 2400より小さい
　3: 2400より大きく 3200より小さい
　4: 3200より大きく 4000より小さい
　5: 4000より大きい

解説

第３四分位数は、上から13番目と14番目の平均です。どちらも、3000円～3400円の階級にあるので、第３四分位数もこの階級にあります。

四分位範囲は、第３四分位数と第１四分位数の差です。 $3400-1800=1600$ と $3000-2200=800$ から、四分位範囲は、800より大きく、1600より小さいことがわかります。

解答

ア：2 (2点)
イ：5 (2点)
ウ：1 (2点)

解答編　つづき

問題

(2) 太郎さんは、東西での地域による食文化の違いを調べるために、52市を東側の地域E（19市）と西側の地域W（33市）の二つに分けて考えることにした。

(i) 地域Eと地域Wについて、かば焼きの支出金額の箱ひげ図を、図２、３のようにそれぞれ作成した。

　かば焼きの支出金額について、図２と図３から読み取れることとして、次の 0 ～ 3 のうち、正しいものは $\dBox{エ}$ である。

$\dbox{エ}$ の解答群

　0: 地域Eにおいて、小さい方から5番目は2000以下である。
　1: 地域Eと地域Wの範囲は等しい。
　2: 中央値は、地域Eより地域Wの方が大きい。
　3: 2600未満の市の割合は、地域Eより地域Wの方が大きい。

解説

(2)(i)
地域Eは19市なので、中央値は下から10番目、第１四分位数は下から5番目となります。左側の箱ひげ図を見ると、第１四分位数は2000より大きい値なので、0は正しくありません。

範囲とは、最大値と最小値の差であり、２つの箱ひげ図を比較すれば、等しくないことがわかります。1は正しくありません。

中央値は、箱の中にある線に対応しており、２つの箱ひげ図を比較すれば、地域Eより地域Wのほうが大きいことがわかります。2が正しいことがわかります。

地域Eは中央値が2600より下なので、半数以上が2600未満です。一方、地域Wは、中央値が2600より上なので、2600未満の市は半数未満です。なので、2600未満の市の割合は、地域Eのほうが地域Wより大きいことがわかります。3は正しくありません。

解答

解答編　つづき

問題

(ii) 太郎さんは、地域Eと地域Wのデータの散らばりの度合いを数値でとらえようと思い、それぞれの分散を考えることにした。地域Eにおけるかば焼きの支出の分散は、地域Eのそれぞれの市におけるかば焼きの支出金額の偏差の $\dBox{オ}$ である。

$\dbox{オ}$ の解答群

　0: 2乗を合計した値
　1: 絶対値を合計した値
　2: 2乗を合計して地域Eの市の数で割った値
　3: 絶対値を合計して地域Eの市の数で割った値
　4: 2乗を合計して地域Eの市の数で割った値の平方根のうち、正のもの
　5: 絶対値を合計して地域Eの市の数で割った値の平方根のうち、正のもの

解説

(ii)
偏差とは、平均からの差のことです。これを２乗して合計し、個数で割ったものが分散です。なので、2が正しいです。

ちなみに、4は、標準偏差のことです。

解答

オ：2 (3点)

解答編　つづき

問題

(3) 太郎さんは、(2)で考えた地域Eにおける、やきとりの支出金額についても調べることにした。

　ここでは地域Eにおいて、やきとりの支出金額が増加すれば、かば焼きの支出金額も増加する傾向があるのではないかと考え、まず図４のように、地域Eにおける、やきとりとかば焼きの支出金額の散布図を作成した。そして、相関係数を計算するために、表１のように平均値、分散、標準偏差および共分散を算出した。ただし、共分散は地域Eのそれぞれの市における、やきとりの支出金額の偏差とかば焼きの支出金額の偏差との積の平均値である。

表１　地域Eにおける、やきとりとかば焼きの支出金額の平均値、分散、標準偏差および共分散

	平均値	分散	標準偏差	共分散
やきとりの支出金額	2810	348100	590	124000
かば焼きの支出金額	2350	324900	570

　表１を用いると、地域Eにおける、やきとりの支出金額とかば焼きの支出金額の相関係数は $\dBox{カ}$ である。

$\dbox{カ}$ については、最も適当なものを、次の 0 ～ 9 のうちから一つ選べ。
　0: $-0.62$
　1: $-0.50$
　2: $-0.37$
　3: $-0.19$
　4: $-0.02$
　5: $0.02$
　6: $0.19$
　7: $0.37$
　8: $0.50$
　9: $0.62$

解説

(3)
相関係数は、共分散をそれぞれの標準偏差で割ればいいので
\begin{eqnarray} \frac{124000}{590\cdot570}=0.3687\cdots \end{eqnarray} となります。

解答