共通テスト 数学I・数学A 2023年度 第3問 解説

【第3問～第5問から2問選択】

問題編

問題

　番号によって区別された複数の球が、何本かのひもでつながれている。ただし、各ひもはその両端で二つの球をつなぐものとする。次の条件を満たす球の塗り分け方（以下、球の塗り方）を考える。

条件

• それぞれの球を、用意した5色（赤、青、黄、緑、紫）のうちのいずれか1色で塗る。
• 1本のひもでつながれた二つの球は異なる色になるようにする。
• 同じ色を何回使ってもよく、また使わない色があってもよい。

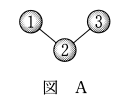
　例えば、図Aでは、三つの球が2本のひもでつながれている。この三つの球を塗るとき、球1の塗り方が5通りあり、球1を塗った後、球2の塗り方は4通りあり、さらに球3の塗り方は4通りある。したがって、球の塗り方の総数は $80$ である。

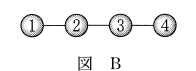
(1) 図Bにおいて、球の塗り方は $\myBox{アイウ}$ 通りある。

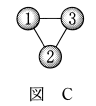
(2) 図Cにおいて、球の塗り方は $\myBox{エオ}$ 通りある。

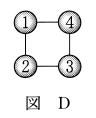
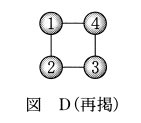
(3) 図Dにおける球の塗り方のうち、赤をちょうど2回使う塗り方は $\myBox{カキ}$ 通りある。

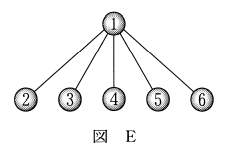
(4) 図Eにおける球の塗り方のうち、赤をちょうど3回使い、かつ青をちょうど2回使う塗り方は $\myBox{クケ}$ 通りある。

(5) 図Dにおいて、球の塗り方の総数を求める。

　そのために、次の構想を立てる。

構想
　図Dと図Fを比較する。

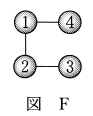
　図Fでは球3と球4が同色になる球の塗り方が可能であるため、図Dよりも図Fの球の塗り方の総数のほうが大きい。

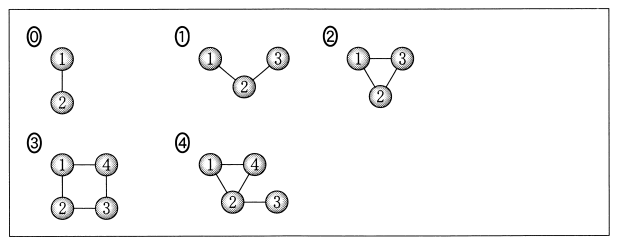
　図Fにおける球の塗り方は、図Bにおける球の塗り方と同じであるため、全部で $\mybox{アイウ}$ 通りある。そのうち球3と球4が同色になる球の塗り方の総数と一致する図として、後の 0 ～ 4 のうち、正しいものは $\dBox{コ}$ である。したがって、図Dにおける球の塗り方は $\myBox{サシス}$ 通りある。

$\dbox{コ}$ の解答群

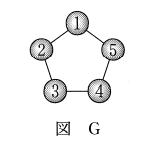
(6) 図Gにおいて、球の塗り方は $\myBox{セソタチ}$ 通りある。

考え方

誘導が丁寧なので、それに従って解いていきましょう。最後の問題は、直前の問題を応用して解きましょう。

解答編

問題

　番号によって区別された複数の球が、何本かのひもでつながれている。ただし、各ひもはその両端で二つの球をつなぐものとする。次の条件を満たす球の塗り分け方（以下、球の塗り方）を考える。

条件

• それぞれの球を、用意した5色（赤、青、黄、緑、紫）のうちのいずれか1色で塗る。
• 1本のひもでつながれた二つの球は異なる色になるようにする。
• 同じ色を何回使ってもよく、また使わない色があってもよい。

　例えば、図Aでは、三つの球が2本のひもでつながれている。この三つの球を塗るとき、球1の塗り方が5通りあり、球1を塗った後、球2の塗り方は4通りあり、さらに球3の塗り方は4通りある。したがって、球の塗り方の総数は $80$ である。

(1) 図Bにおいて、球の塗り方は $\myBox{アイウ}$ 通りある。

解説

(1) 1の球の塗り方が5通り、2と3と4の球はそれぞれ4通りあるので、\[ 5\cdot4\cdot4\cdot4=320 \]通りとなります。

解答

アイウ：320 (3点)

解答編　つづき

問題

(2) 図Cにおいて、球の塗り方は $\myBox{エオ}$ 通りある。

解説

(2) 1の球の塗り方が5通り、2の塗り方は、1で使ってない色だったら何でもいいので4通りです。3の塗り方は、1と2で使った色以外だったらいいので、3通りです。なので\[ 5\cdot4\cdot3=60 \]通りです。

解答

エオ：60 (3点)

解答編　つづき

問題

(3) 図Dにおける球の塗り方のうち、赤をちょうど2回使う塗り方は $\myBox{カキ}$ 通りある。

解説

(3) 赤を2回使うということは、1と3だけを赤にするか、2と4だけを赤にするかの2通りです。赤を塗る2つを決めたとき、残りの球は、赤以外だったら何でもいいので4通りずつ塗り方があります。なので、\[ 2\cdot4\cdot4=32 \]通りです。

解答

カキ：32 (3点)

解答編　つづき

問題

(4) 図Eにおける球の塗り方のうち、赤をちょうど3回使い、かつ青をちょうど2回使う塗り方は $\myBox{クケ}$ 通りある。

解説

(4) 1を赤で塗ってしまうと、2から6を赤で塗ることはできません。また、1を青で塗ると、2から6を青で塗ることはできません。なので、1は、赤でも青でもない色にしないといけません。

そうすると、2から6までの5個の球の中で、赤が3個、青が2個になる場合を考えればいいとわかります。どの3個を赤にするかは自由に選べるので、5個から3個選ぶ場合の数を考えればいいです。残りは自動的に青色になります。

以上から、塗り方は\[ 3\cdot {}_{5}\mathrm{C}_3=3\cdot 10=30 \]通りだとわかります。

解答

クケ：30 (3点)

解答編　つづき

問題

(5) 図Dにおいて、球の塗り方の総数を求める。

　そのために、次の構想を立てる。

構想
　図Dと図Fを比較する。

　図Fでは球3と球4が同色になる球の塗り方が可能であるため、図Dよりも図Fの球の塗り方の総数のほうが大きい。

　図Fにおける球の塗り方は、図Bにおける球の塗り方と同じであるため、全部で $\mybox{アイウ}$ 通りある。そのうち球3と球4が同色になる球の塗り方の総数と一致する図として、後の 0 ～ 4 のうち、正しいものは $\dBox{コ}$ である。したがって、図Dにおける球の塗り方は $\myBox{サシス}$ 通りある。

$\dbox{コ}$ の解答群

解説

(5) 図Fの塗り方は、図Bと同じ320通りです。

図Dで、3と4の球が同じ色になってしまう塗り方は、3と4の球を同一視したのと同じ図である、2番のケースと同じ総数になります。これは(2)で求めた通り、60通りです。

以上から、\[ 320-60=260 \]通りだとわかります。

解答

コ：2 (3点)
サシス：260 (2点)

解答編　つづき

問題

(6) 図Gにおいて、球の塗り方は $\myBox{セソタチ}$ 通りある。

解説

(6) (5)と同じように考えます。

4と5の球がつながっていなければ、塗り方の総数は\[ 5\cdot4\cdot4\cdot4\cdot4=1280 \]通りです。

ここから、4と5の球の色が同じケースを引けばいいです。これは、4と5の球をくっつけて同一視したと考えれば、図Dと同じだと考えられます。つまり、(5)で求めたように、260通りです。

以上から、\[ 1280-260=1020 \]通りだとわかります。

解答

セソタチ：1020 (3点)