京都大学 理学部特色入試 2022年度 第4問 解説
(2021年11月に行われた特色入試の問題です。2022年に行われた特色入試の問題はこちら)
問題編
問題
$0$ 以上 $1$ 未満の実数 $p$ を固定する。 $n$ を正の整数とし、 $xy$ 平面上の領域 $D_n$ を $x+y\leqq n$ で定める。 $xy$ 平面上の点 $P_0(0, n)$ から始まる点列 $P_0,P_1,P_2,\ldots$ を以下の条件を満たすように定める。
(A) $P_k(x_k,y_k)$ が $y_k\gt 0$ を満たすならば、
(i) 確率 $p$ で $P_{k+1}$ を $(x_k+1,y_k)$ とおく。
(ii) 確率 $1-p$ で $P_{k+1}$ を $(x_k,y_k-1)$ とおく。
(B) $P_k(x_k,y_k)$ が $y_k=0$ を満たすならば、 $P_{k+1}$ を $P_k$ とおく。このとき、以下の設問に答えよ。
(1) $p=\dfrac{1}{2}$ のとき、 $P_{n+k}$ が $(k,0)$ となる確率を $p_{n,k}$ とする。このとき\[ \sum_{k=0}^{\infty} kp_{n,k} \]を求めよ。
(2) 各々の $n$ に対し、上の操作で実現可能な点列 $P_0(0,n), P_1,P_2,\ldots,P_{2n}$ で、これらすべての点が $D_n$ に属するものの総数を $C_n$ とする。また、 $C_0=1$ とする。このとき、\[ C_{n+1}=\sum_{k=0}^n C_k C_{n-k} \]が成り立つことを示せ。
(3) 点列 $P_0(0,n),P_1,P_2,P_3,\ldots$ のすべての点が領域 $D_n$ に属する確率を $q_n$ とする。このとき、\[ \lim_{n\to\infty} q_n \]を $p$ を用いて表せ。
ただし、正の実数の列 $\{a_j\}$ が、任意の正の整数 $m$ に対して $\displaystyle \sum_{j=1}^m a_j\leqq 1$ を満たすとき、以下が成り立つことを用いてもよい。
・極限 $\displaystyle \lim_{m\to\infty} \sum_{j=1}^m a_j$ が存在する。この極限値を $a$ とすると $a\leqq 1$
・$a$ の値は実数の列 $\{a_n\}$ の順番を入れ替えたとしても変わらない。
考え方
(1)は、二項係数を変形して和を求めていきます。
(2)は、カタラン数のことで、特色入試を受ける人なら見たことはあるでしょう。よくある最短経路と問題の設定は異なる(この問題では $x$ 軸にたどりついた後はもう動かない)ので注意しましょう。
(3)は、極限が存在することを用いていいと言われているので、これを使いましょう。(2)の式も利用して、極限を2通りの方法で表せば、極限値に関する方程式が得られます。細かい議論や式変形が多いので、答えを求めるのは大変です。
解答編
問題
$0$ 以上 $1$ 未満の実数 $p$ を固定する。 $n$ を正の整数とし、 $xy$ 平面上の領域 $D_n$ を $x+y\leqq n$ で定める。 $xy$ 平面上の点 $P_0(0, n)$ から始まる点列 $P_0,P_1,P_2,\ldots$ を以下の条件を満たすように定める。
(A) $P_k(x_k,y_k)$ が $y_k\gt 0$ を満たすならば、
(i) 確率 $p$ で $P_{k+1}$ を $(x_k+1,y_k)$ とおく。
(ii) 確率 $1-p$ で $P_{k+1}$ を $(x_k,y_k-1)$ とおく。
(B) $P_k(x_k,y_k)$ が $y_k=0$ を満たすならば、 $P_{k+1}$ を $P_k$ とおく。このとき、以下の設問に答えよ。
(1) $p=\dfrac{1}{2}$ のとき、 $P_{n+k}$ が $(k,0)$ となる確率を $p_{n,k}$ とする。このとき\[ \sum_{k=0}^{\infty} kp_{n,k} \]を求めよ。
解答
(1)
$P_{n+k}$ が $(k,0)$ となるのは、 $P_{n+k-1}$ が $(k,1)$ であって、次の操作で下の点を選ぶときであり、そのときに限る。よって、こうなる確率は
\begin{eqnarray}
p_{n,k}
&=&
{}_{n-1+k} \mathrm{C}_{k} \cdot \frac{1}{2^k} \cdot\frac{1}{2^{n-1} }\cdot \frac{1}{2} \\[5pt]
&=&
{}_{n+k-1} \mathrm{C}_{k} \cdot \frac{1}{2^{n+k} } \\[5pt]
\end{eqnarray}と書ける。よって、 $k\geqq 1$ のとき、
\begin{eqnarray}
kp_{n,k}
&=&
k\cdot {}_{n+k-1} \mathrm{C}_{k} \cdot \frac{1}{2^{n+k} } \\[5pt]
&=&
k\cdot \frac{(n+k-1)!}{(n-1)!k!} \cdot \frac{1}{2^{n+k} } \\[5pt]
&=&
\frac{(n+k-1)!}{(n-1)!(k-1)!} \cdot \frac{1}{2^{n+k} } \\[5pt]
&=&
n\cdot \frac{(n+k-1)!}{n!(k-1)!} \cdot \frac{1}{2^{n+k} } \\[5pt]
&=&
n\cdot {}_{n+k-1} \mathrm{C}_{k-1} \cdot \frac{1}{2^{n+k} } \\[5pt]
&=&
np_{n+1,k-1}
\end{eqnarray}となる。これより、正の整数 $M$ に対し
\begin{eqnarray}
\sum_{k=0}^{M} kp_{n,k}
&=&
\sum_{k=1}^{M} kp_{n,k} \\[5pt]
&=&
\sum_{k=1}^{M} n p_{n+1,k-1} \\[5pt]
&=&
n\sum_{k=0}^{M-1} p_{n+1,k} \\[5pt]
\end{eqnarray}が成り立つ。
ここで、 $\displaystyle \sum_{k=0}^{M-1} p_{n+1,k}$ は、点 $(0,n+1)$ から始めて、問題文にある操作を繰り返したとき、 $P_{n+M}$ の $y$ 座標が $0$ になる確率を表している。そのため、 $\displaystyle 1-\sum_{k=0}^{M-1} p_{n+1,k}$ は、 $n+M$ 回の操作後でも $y$ 座標が正である確率を表している。
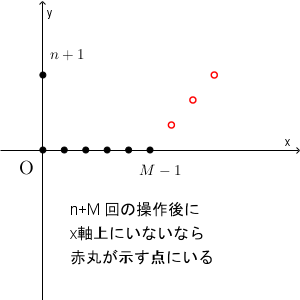
以上から
\begin{eqnarray}
& &
\sum_{k=0}^{\infty} kp_{n,k} \\[5pt]
&=&
\lim_{M\to\infty} n\sum_{k=0}^{M-1} p_{n+1,k} \\[5pt]
&=&
n \\[5pt]
\end{eqnarray}となる。
((1)終)
解答編 続き
問題
(2) 各々の $n$ に対し、上の操作で実現可能な点列 $P_0(0,n), P_1,P_2,\ldots,P_{2n}$ で、これらすべての点が $D_n$ に属するものの総数を $C_n$ とする。また、 $C_0=1$ とする。このとき、\[ C_{n+1}=\sum_{k=0}^n C_k C_{n-k} \]が成り立つことを示せ。
解答
(2)
$P_{0}(0,n+1)$ のとき、 $P_1$ が領域 $D_n$ に属するとすると、点 $(0,n)$ となるしかない。これ以降、はじめて直線 $y=-x+(n+1)$ 上の点になるときで場合分けをする。
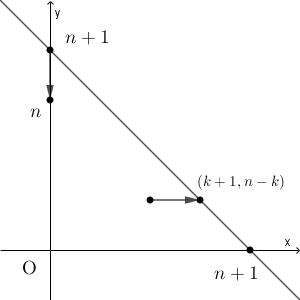
$y$ 座標が $n-k$ のとき( $k$ は $0$ 以上 $n-1$ 以下の整数)にはじめて直線 $y=-x+(n+1)$ 上の点になるとする。このとき、 $P_{2k+1}(k,n-k)$ かつ $P_{2k+2}(k+1,n-k)$ となっている。また、 $P_1$ から $P_{2k+1}$ までは、 $y\leqq -x+n$ の領域内にある。よって、 $P_1$ から $P_{2k+1}$ の選び方は $C_k$ 通りである。また、 $P_{2k+2}(k+1,n-k)$ から $P_{2n}$ までは、「点 $(0,n-k)$ からはじめた場合」と同一視できるので、選び方は $C_{n-k}$ 通りである。
また、直線 $y=-x+(n+1)$ 上の点にならない場合もある。こうなるのは、 $P_1$ 以降、つねに $y\leqq -x+n$ の領域内にあるときなので、点列の選び方は $C_n$ 通りである。
よって、\[ C_{n+1}=\sum_{k=0}^{n-1} C_k C_{n-k}+C_n=\sum_{k=0}^n C_k C_{n-k} \]が成り立つ。
((2)終)
解答編 続き
問題
(3) 点列 $P_0(0,n),P_1,P_2,P_3,\ldots$ のすべての点が領域 $D_n$ に属する確率を $q_n$ とする。このとき、\[ \lim_{n\to\infty} q_n \]を $p$ を用いて表せ。
ただし、正の実数の列 $\{a_j\}$ が、任意の正の整数 $m$ に対して $\displaystyle \sum_{j=1}^m a_j\leqq 1$ を満たすとき、以下が成り立つことを用いてもよい。
・極限 $\displaystyle \lim_{m\to\infty} \sum_{j=1}^m a_j$ が存在する。この極限値を $a$ とすると $a\leqq 1$
・$a$ の値は実数の列 $\{a_n\}$ の順番を入れ替えたとしても変わらない。
解答
(3)
$p=0$ のときは明らかに $\displaystyle \lim_{n\to\infty}q_n=1$ である。以下では $p\ne 0$ とする。
$P_0(0,n+1)$ とし、どれかの点が領域 $D_{n+1}$ に属さない確率 $1-q_{n+1}$ を考える。
はじめて領域 $D_{n+1}$ から出るときで場合分けをする。 $j$ を $0\leqq j\leqq n$ を満たす整数として、 $y$ 座標が $n+1-j$ のときにはじめて領域 $D_{n+1}$ から出るとする。このとき、 $P_{2j}$ まで領域 $D_{n+1}$ 内にあり、 $P_{2j+1}(j, n+1-j)$ かつ $P_{2j+2}(j+1,n+1-j)$ となる。また、このような点列は $C_j$ 通りある。これら以外に $D_{n+1}$ から出ることはないので、 $1-q_{n+1}$ は
\begin{eqnarray}
\sum_{j=0}^n p^j(1-p)^j \cdot C_j \cdot p
\end{eqnarray}と書ける。
問題文にある内容から、上の和で $n\to\infty$ とすると、$1$ 以下の、ある値に収束する。この収束値を $\alpha_p$ とおく。
また、上の式で $p$ を $1-p$ に置き換えたものは
\begin{eqnarray}
& &
\sum_{j=0}^n p^j(1-p)^j \cdot C_j \cdot (1-p) \\[5pt]
&=&
\frac{1-p}{p} \cdot \sum_{j=0}^n p^j(1-p)^j \cdot C_j \cdot p \\[5pt]
\end{eqnarray}と書けることから
\begin{eqnarray}
\alpha_{1-p}&=&\frac{1-p}{p}\alpha_{p} \\[5pt]
\alpha_p&=&\frac{p}{1-p}\alpha_{1-p}
\end{eqnarray}が成り立つ。これより、以下では、まず、 $\dfrac{1}{2} \leqq p\lt 1$ の場合を考える。なお、 $\alpha_p$ の $p$ を略して書く。
\begin{eqnarray}
& &
1-q_{n+1} \\[5pt]
&=&
\sum_{j=0}^n p^j(1-p)^j \cdot C_j \cdot p \\[5pt]
&=&
p+p\sum_{j=1}^n p^j(1-p)^j \cdot C_j \\[5pt]
&=&
p+p\sum_{j=1}^n p^j(1-p)^j \sum_{k=0}^{j-1} C_k C_{j-1-k} \\[5pt]
&=&
p+p\sum_{j=0}^{n-1} p^{j+1}(1-p)^{j+1} \sum_{k=0}^j C_k C_{j-k} \\[5pt]
&=&
p+p^2(1-p)\sum_{j=0}^{n-1} \sum_{k=0}^j p^j(1-p)^j C_k C_{j-k} \\[5pt]
\end{eqnarray}
ここで、 $0\leqq j\leqq n-1$ の各 $j$ に対し $k=0$ から $k=j$ としたものまで足すことは、 $0\leqq k \leqq n-1$ の各 $k$ に対し $j=k$ から $j=n-1$ としたものまで足すことに等しい。
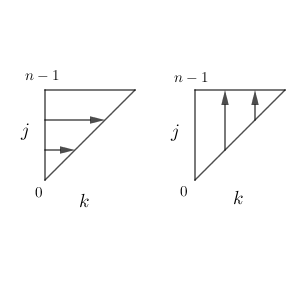
よって、先ほどの式をさらに変形して
\begin{eqnarray}
& &
1-q_{n+1} \\[5pt]
&=&
p+p^2(1-p)\sum_{j=0}^{n-1} \sum_{k=0}^j p^j(1-p)^j C_k C_{j-k} \\[5pt]
&=&
p+p^2(1-p)\sum_{k=0}^{n-1} \sum_{j=k}^{n-1} p^j(1-p)^j C_k C_{j-k} \\[5pt]
&=&
p+p^2(1-p)\sum_{k=0}^{n-1} \sum_{j=0}^{n-1-k} p^{j+k}(1-p)^{j+k} C_k C_j \\[5pt]
&=&
p+p^2(1-p)\sum_{k=0}^{n-1} p^k(1-p)^k C_k \sum_{j=0}^{n-1-k} p^j(1-p)^j C_j \\[5pt]
\end{eqnarray}となる。
ここで、 $0\leqq k \leqq n-1$ の各 $k$ に対し $j=0$ から $j=n-1-k$ としたものまでを足すことは、下の赤い三角形内に含まれるすべての整数の組 $(k, j)$ について足すことになる。
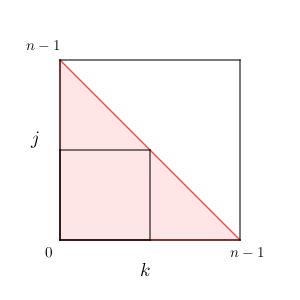
各項は非負なので、これは「 $0\leqq k \leqq n-1$, $0\leqq j \leqq n-1$ について足したもの」以下で、「 $0\leqq k \leqq \left[\frac{n-1}{2}\right]$, $0\leqq j \leqq \left[\frac{n-1}{2}\right]$ について足したもの」以上である。ここで $n\to \infty$ とすると
\begin{eqnarray}
& &
p+p^2(1-p)\sum_{k=0}^{n-1} p^k(1-p)^k C_k \sum_{j=0}^{n-1} p^j(1-p)^j C_j \\[5pt]
&\to&
p+p^2(1-p)\cdot \frac{\alpha}{p} \cdot \frac{\alpha}{p} \\[5pt]
&=&
p+(1-p)\alpha^2 \\[5pt]
\end{eqnarray}であり、
\begin{eqnarray}
& &
p+p^2(1-p)\sum_{k=0}^{[(n-1)/2]} p^k(1-p)^k C_k \sum_{j=0}^{[(n-1)/2]} p^j(1-p)^j C_j \\[5pt]
&\to&
p+(1-p)\alpha^2 \\[5pt]
\end{eqnarray}となることから、はさみうちの原理により
\begin{eqnarray}
\alpha
&=&
\lim_{n\to\infty} (1-q_{n+1}) \\[5pt]
&=&
\lim_{n\to\infty} \left\{ p+p^2(1-p)\sum_{k=0}^{n-1} p^k(1-p)^k C_k \sum_{j=0}^{n-1-k} p^j(1-p)^j C_j \right\} \\[5pt]
&=&
p+(1-p)\alpha^2 \\[5pt]
\end{eqnarray}となる。これより、 $\alpha$ は\[ (1-p)\alpha^2-\alpha+p=0 \]を満たすので、
\begin{eqnarray}
\alpha &=& \frac{1\pm\sqrt{1-4(1-p)p} }{2(1-p)} \\[5pt]
&=& \frac{1\pm |2p-1|}{2(1-p)} \\[5pt]
\end{eqnarray}より、 $\alpha=1,\dfrac{p}{1-p}$ となる。ただし、 $\dfrac{1}{2} \lt p\lt 1$ のときは $\dfrac{p}{1-p}\gt 1$ なので $\alpha\leqq 1$ に矛盾するので、 $\alpha=1$ である。また、 $p=\dfrac{1}{2}$ のときも $\alpha=1$ である。
よって、 $\dfrac{1}{2} \leqq p\lt 1$ のときは
\begin{eqnarray}
\lim_{n\to\infty} q_n=1-\alpha=0
\end{eqnarray}となる。また、 $0 \lt p\lt \dfrac{1}{2}$ のときは
\begin{eqnarray}
\lim_{n\to\infty} q_n=1-\frac{p}{1-p}\cdot \alpha_{1-p}=\frac{1-2p}{1-p}
\end{eqnarray}となる。これは $p=0$ のときも成り立つ。
以上から、 $0\leqq p \lt \dfrac{1}{2}$ のときは\[ \lim_{n\to\infty} q_n=\frac{1-2p}{1-p} \]であり、$\dfrac{1}{2}\leqq p \lt 1$ のときは\[ \lim_{n\to\infty} q_n=0 \]となる。
(終)





